
William Brouncker, 2nd Viscount Brouncker
Encyclopedia
William Brouncker, 2nd Viscount Brouncker, PRS (1620 – 5 April 1684) was an English mathematician
.
Brouncker obtained a DM
at the University of Oxford
in 1647. He was one of the founders and the first President
of the Royal Society
. In 1662, he became Chancellor
to Queen Catherine
, then chief of the Saint Catherine's Hospital. He was appointed one of the Commissioners of the Navy in 1664 and his career can be traced in the Diary of Samuel Pepys; despite frequent disagreements Pepys on the whole respected Brouncker more than most of his colleagues. Brouncker never married but lived for many years with the actress Abigail Williams ( much to Pepys' disgust ) and left most of his property to her. His title passed to his brother Henry , one of the most detested men of the era. His mathematical work concerned in particular the calculations of the lengths of the parabola
and cycloid
, and the quadrature
of the hyperbola
, which requires approximation of the natural logarithm
function by infinite series. He was the first European to solve what is now known as Pell's equation
. He was the first in England to take interest in generalized continued fraction
s and, following the work of John Wallis, he provided development in the generalized continued fraction of pi
.
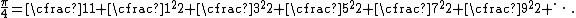
The convergents are related to the Leibniz formula for pi: for instance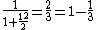
and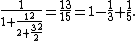
Because of its slow convergence Brouncker's formula is not useful for practical computations of π.
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
.
Brouncker obtained a DM
Doctor of Medicine
Doctor of Medicine is a doctoral degree for physicians. The degree is granted by medical schools...
at the University of Oxford
University of Oxford
The University of Oxford is a university located in Oxford, United Kingdom. It is the second-oldest surviving university in the world and the oldest in the English-speaking world. Although its exact date of foundation is unclear, there is evidence of teaching as far back as 1096...
in 1647. He was one of the founders and the first President
President of the Royal Society
The president of the Royal Society is the elected director of the Royal Society of London. After informal meetings at Gresham College, the Royal Society was founded officially on 15 July 1662 for the encouragement of ‘philosophical studies’, by a royal charter which nominated William Brouncker as...
of the Royal Society
Royal Society
The Royal Society of London for Improving Natural Knowledge, known simply as the Royal Society, is a learned society for science, and is possibly the oldest such society in existence. Founded in November 1660, it was granted a Royal Charter by King Charles II as the "Royal Society of London"...
. In 1662, he became Chancellor
Chancellor
Chancellor is the title of various official positions in the governments of many nations. The original chancellors were the Cancellarii of Roman courts of justice—ushers who sat at the cancelli or lattice work screens of a basilica or law court, which separated the judge and counsel from the...
to Queen Catherine
Catherine of Braganza
Catherine of Braganza was a Portuguese infanta and queen consort of England, Scotland and Ireland as the wife of King Charles II.She married the king in 1662...
, then chief of the Saint Catherine's Hospital. He was appointed one of the Commissioners of the Navy in 1664 and his career can be traced in the Diary of Samuel Pepys; despite frequent disagreements Pepys on the whole respected Brouncker more than most of his colleagues. Brouncker never married but lived for many years with the actress Abigail Williams ( much to Pepys' disgust ) and left most of his property to her. His title passed to his brother Henry , one of the most detested men of the era. His mathematical work concerned in particular the calculations of the lengths of the parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
and cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
, and the quadrature
Quadrature (mathematics)
Quadrature — historical mathematical term which means calculating of the area. Quadrature problems have served as one of the main sources of mathematical analysis.- History :...
of the hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
, which requires approximation of the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
function by infinite series. He was the first European to solve what is now known as Pell's equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
. He was the first in England to take interest in generalized continued fraction
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
s and, following the work of John Wallis, he provided development in the generalized continued fraction of pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
.
Brouncker's formula
This formula provides a development of π/4 in a generalized continued fraction: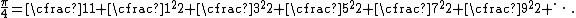
The convergents are related to the Leibniz formula for pi: for instance
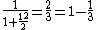
and
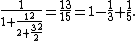
Because of its slow convergence Brouncker's formula is not useful for practical computations of π.

