
Wilkie's theorem
Encyclopedia
In mathematics
, Wilkie's theorem is a result by Alex Wilkie
about the theory of ordered field
s with an exponential function
, or equivalently about the geometric nature of exponential varieties.
, Wilkie's theorem deals with the language Lexp = (+,−,·,<,0,1,ex), the language of ordered ring
s with an exponential function ex. Suppose φ(x1,...,xm) is a formula in this language, then Wilkie's theorem states that there is an integer n ≥ m and polynomials f1,...,fr ∈ Z[x1,...,xn,ex1,...,exn] such that φ(x1,...,xn) is equivalent to the existential formula
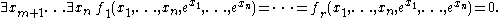
Thus, while this theory does not have full quantifier elimination
, formulae can be put in a particularly simple form. This result proves that the theory of the structure Rexp, that is the real ordered field with the exponential function
, is model complete.
In terms of analytic geometry, the theorem states that any definable set
in the above language — in particular the complement of an exponential variety — is in fact a projection of an exponential variety. An exponential variety over a field K is the set of points in Kn where a finite collection of exponential polynomial
s simultaneously vanish. Wilkie's theorem states that if we have any definable set in an Lexp structure K = (K,+,−,·,0,1,ex), say X ⊂ Km, then there will be an exponential variety in some higher dimension Kn such that the projection of this variety down onto Km will be precisely X.
on Rm restricted to the closed unit cube [0,1]m. Gabrielov's theorem states that any formula in this language is equivalent to an existential one, as above. Hence the theory of the real ordered field with restricted analytic functions is model complete.
s. In particular the theory of the real ordered field with restricted, totally defined pfaffian functions is model complete. Wilkie's approach for this latter result is somewhat different to his proof of Wilkie's theorem, and the result that allowed him to show that the Pfaffian structure is model complete is sometimes known as Wilkie's theorem of the complement.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Wilkie's theorem is a result by Alex Wilkie
Alex Wilkie
Alex Wilkie FRS is a British mathematician known for his contributions to Model theory and logic. Previously Reader in Mathematical Logic at the University of Oxford, he was appointed to the Fielden Chair of Pure Mathematics at the University of Manchester in 2007.Wilkie attended Aylesbury...
about the theory of ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
s with an exponential function
Exponential field
In mathematics, an exponential field is a field that has an extra operation on its elements which extends the usual idea of exponentiation.-Definition:...
, or equivalently about the geometric nature of exponential varieties.
Formulations
In terms of model theoryModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, Wilkie's theorem deals with the language Lexp = (+,−,·,<,0,1,ex), the language of ordered ring
Ordered ring
In abstract algebra, an ordered ring is a commutative ring R with a total order ≤ such that for all a, b, and c in R:* if a ≤ b then a + c ≤ b + c.* if 0 ≤ a and 0 ≤ b then 0 ≤ ab....
s with an exponential function ex. Suppose φ(x1,...,xm) is a formula in this language, then Wilkie's theorem states that there is an integer n ≥ m and polynomials f1,...,fr ∈ Z[x1,...,xn,ex1,...,exn] such that φ(x1,...,xn) is equivalent to the existential formula
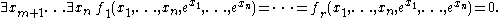
Thus, while this theory does not have full quantifier elimination
Quantifier elimination
Quantifier elimination is a concept of simplification used in mathematical logic, model theory, and theoretical computer science. One way of classifying formulas is by the amount of quantification...
, formulae can be put in a particularly simple form. This result proves that the theory of the structure Rexp, that is the real ordered field with the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, is model complete.
In terms of analytic geometry, the theorem states that any definable set
Definable set
In mathematical logic, a definable set is an n-ary relation on the domain of a structure whose elements are precisely those elements satisfying some formula in the language of that structure...
in the above language — in particular the complement of an exponential variety — is in fact a projection of an exponential variety. An exponential variety over a field K is the set of points in Kn where a finite collection of exponential polynomial
Exponential polynomial
In mathematics, exponential polynomials are functions on fields, rings, or abelian groups that take the form of polynomials in a variable and an exponential function.-In fields:...
s simultaneously vanish. Wilkie's theorem states that if we have any definable set in an Lexp structure K = (K,+,−,·,0,1,ex), say X ⊂ Km, then there will be an exponential variety in some higher dimension Kn such that the projection of this variety down onto Km will be precisely X.
Gabrielov's theorem
The result can be considered as a variation of Gabrielov's theorem. This earlier theorem, by Andrei Gabrielov, dealt with sub-analytic sets, or the language Lan of ordered rings with a function symbol for each proper analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
on Rm restricted to the closed unit cube [0,1]m. Gabrielov's theorem states that any formula in this language is equivalent to an existential one, as above. Hence the theory of the real ordered field with restricted analytic functions is model complete.
Intermediate results
Gabrielov's theorem applies to the real field with all restricted analytic functions adjoined, whereas Wilkie's theorem removes the need to restrict the function, but only allows one to add the exponential function. As an intermediate result Wilkie asked when the complement of a sub-analytic set could be defined using the same analytic functions that described the original set. It turns out the required functions are the pfaffian functionPfaffian function
In mathematics, the Pfaffian functions are a certain class of functions introduced by Askold Georgevich Khovanskiǐ in the 1970s. They are named after German mathematician Johann Pfaff.-Basic definition:...
s. In particular the theory of the real ordered field with restricted, totally defined pfaffian functions is model complete. Wilkie's approach for this latter result is somewhat different to his proof of Wilkie's theorem, and the result that allowed him to show that the Pfaffian structure is model complete is sometimes known as Wilkie's theorem of the complement.

