
Pfaffian function
Encyclopedia
In mathematics
, the Pfaffian functions are a certain class of functions introduced by Askold Georgevich Khovanskiǐ in the 1970s. They are named after German mathematician Johann Pfaff.
, when differentiated
, give a result which can be written in terms of the original function. Perhaps the simplest example is the exponential function
, f(x) = ex. If we differentiate this function we get ex again, that is
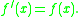
Another example of a function like this is the reciprocal function, g(x) = 1/x. If we differentiate this function we will see that

Other functions may not have the above property, but their derivative may be written in terms of functions like those above. For example if we take the function h(x) = exlog(x) then we see
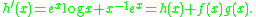
Functions like these form the links in a so-called Pfaffian chain. Such a chain is a sequence of functions, say f1, f2, f3, etc., with the property that if we differentiate any of the functions in this chain then the result can be written in terms of the function itself and all the functions preceding it in the chain (specifically as a polynomial
in those functions and the variables involved). So with the functions above we have that f, g, h is a Pfaffian chain.
A Pfaffian function is then just a polynomial in the functions appearing in a Pfaffian chain and the function argument. So with the Pfaffian chain just mentioned, functions such as F(x) = x3f(x)2 − 2g(x)h(x) are Pfaffian.
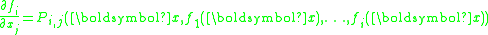
for i = 1,…,r where Pi,j ∈ R[x1,...,xn,y1,...,yi] are polynomials of degree ≤ α. A function f on U is called a Pfaffian function of order r and degree (α,β) if
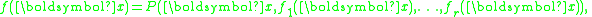
where P ∈ R[x1,...,xn,y1,...,yr] is a polynomial of degree at most β ≥ 1. The numbers r, α, and β are collectively known as the format of the Pfaffian function, and give a useful measure of its complexity.
In the 1990s, Alex Wilkie
showed that one has the same result if instead of adding every analytic function, one just adds the exponential function to R to get the ordered real field with exponentiation, Rexp, a result known as Wilkie's theorem
. Wilkie then tackled the question of which finite sets of functions could be added to R to get this result. It turned out that adding any Pfaffian chain restricted to the box [0,1]m would give the same result. In particular one may add all Pfaffian functions to R to get the structure RPfaff as an intermediate result between Gabrielov's result and Wilkie's theorem
. Since the exponential function is a Pfaffian chain by itself, the result on exponentiation can be viewed as a special case of this latter result.
This result of Wilkie's proved that the structure RPfaff is an o-minimal structure.
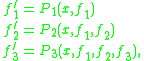
and so on. If this triangularity condition is relaxed so that the derivative of each function in the chain is a polynomial in all the other functions in the chain, then the chain of functions is known as a Noetherian chain, and a function constructed as a polynomial in this chain is called a Noetherian function. So, for example, a Noetherian chain of order three is composed of three functions f1, f2, f3, satisfying the equations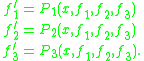
The name stems from the fact that the ring
generated by the functions in such a chain is Noetherian
.
Any Pfaffian chain is also a Noetherian chain; the extra variables in each polynomial are simply redundant in this case. But not every Noetherian chain is Pfaffian. If we take f1(x) = sin(x) and f2(x) = cos(x) then we have the equations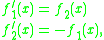
and these hold for all real numbers x, so f1,f2 is a Noetherian chain on all of R. But there is no polynomial P(x,y) such that the derivative of sin(x) can be written as P(x,sin(x)), and so this chain is not Pfaffian.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Pfaffian functions are a certain class of functions introduced by Askold Georgevich Khovanskiǐ in the 1970s. They are named after German mathematician Johann Pfaff.
Basic definition
Some functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, when differentiated
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
, give a result which can be written in terms of the original function. Perhaps the simplest example is the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, f(x) = ex. If we differentiate this function we get ex again, that is
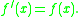
Another example of a function like this is the reciprocal function, g(x) = 1/x. If we differentiate this function we will see that

Other functions may not have the above property, but their derivative may be written in terms of functions like those above. For example if we take the function h(x) = exlog(x) then we see
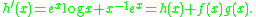
Functions like these form the links in a so-called Pfaffian chain. Such a chain is a sequence of functions, say f1, f2, f3, etc., with the property that if we differentiate any of the functions in this chain then the result can be written in terms of the function itself and all the functions preceding it in the chain (specifically as a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in those functions and the variables involved). So with the functions above we have that f, g, h is a Pfaffian chain.
A Pfaffian function is then just a polynomial in the functions appearing in a Pfaffian chain and the function argument. So with the Pfaffian chain just mentioned, functions such as F(x) = x3f(x)2 − 2g(x)h(x) are Pfaffian.
Rigorous definition
Let U be an open domain in Rn. A Pfaffian chain of order r ≥ 0 and degree α ≥ 1 in U is a sequence of real analytic functions f1,…, fr in U satisfying differential equations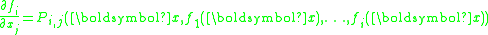
for i = 1,…,r where Pi,j ∈ R[x1,...,xn,y1,...,yi] are polynomials of degree ≤ α. A function f on U is called a Pfaffian function of order r and degree (α,β) if
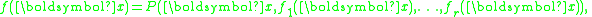
where P ∈ R[x1,...,xn,y1,...,yr] is a polynomial of degree at most β ≥ 1. The numbers r, α, and β are collectively known as the format of the Pfaffian function, and give a useful measure of its complexity.
Examples
- The most trivial examples of Pfaffian functions are the polynomials in R[X]. Such a function will be a polynomial in a Pfaffian chain of order r = 0, that is the chain with no functions. Such a function will have α = 0 and β equal to the degree of the polynomial.
- Perhaps the simplest nontrivial Pfaffian function is f(x) = ex. This is Pfaffian with order r = 1 and α = β = 1 due to the equation f ′ = f.
- Inductively, one may define f1(x) = exp(x) and fm+1(x) = exp(fm(x)) for 1 ≤ m < r. Then fm′ = f1f2···fm. So this is a Pfaffian chain of order r and degree α = r.
- All of the algebraic functions are Pfaffian on suitable domains as are the hyperbolic functionHyperbolic functionIn mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s. The trigonometric functions on bounded intervals are Pfaffian, but they must be formed indirectly. For example, the function cos(x) is a polynomial in the Pfaffian chain tan(x/2), cos2(x/2) on the interval (−π,π).
- In fact all the elementary functions and Liouville functions are Pfaffian.
In model theory
Consider the structure R = (R,+,−,·,<,0,1), the ordered field of real numbers. In the 1960s Andrei Gabrielov proved that the structure obtained by starting with R and adding a function symbol for every analytic function restricted to the unit box [0,1]m is model complete. That is, any set definable in this structure Ran was just the projection of some higher dimensional set defined by identities and inequalities involving these restricted analytic functions.In the 1990s, Alex Wilkie
Alex Wilkie
Alex Wilkie FRS is a British mathematician known for his contributions to Model theory and logic. Previously Reader in Mathematical Logic at the University of Oxford, he was appointed to the Fielden Chair of Pure Mathematics at the University of Manchester in 2007.Wilkie attended Aylesbury...
showed that one has the same result if instead of adding every analytic function, one just adds the exponential function to R to get the ordered real field with exponentiation, Rexp, a result known as Wilkie's theorem
Wilkie's theorem
In mathematics, Wilkie's theorem is a result by Alex Wilkie about the theory of ordered fields with an exponential function, or equivalently about the geometric nature of exponential varieties.-Formulations:...
. Wilkie then tackled the question of which finite sets of functions could be added to R to get this result. It turned out that adding any Pfaffian chain restricted to the box [0,1]m would give the same result. In particular one may add all Pfaffian functions to R to get the structure RPfaff as an intermediate result between Gabrielov's result and Wilkie's theorem
Wilkie's theorem
In mathematics, Wilkie's theorem is a result by Alex Wilkie about the theory of ordered fields with an exponential function, or equivalently about the geometric nature of exponential varieties.-Formulations:...
. Since the exponential function is a Pfaffian chain by itself, the result on exponentiation can be viewed as a special case of this latter result.
This result of Wilkie's proved that the structure RPfaff is an o-minimal structure.
Noetherian functions
The equations above that define a Pfaffian chain are said to satisfy a triangular condition, since the derivative of each successive function in the chain is a polynomial in one extra variable. Thus if they are written out in turn a triangular shape appears: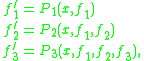
and so on. If this triangularity condition is relaxed so that the derivative of each function in the chain is a polynomial in all the other functions in the chain, then the chain of functions is known as a Noetherian chain, and a function constructed as a polynomial in this chain is called a Noetherian function. So, for example, a Noetherian chain of order three is composed of three functions f1, f2, f3, satisfying the equations
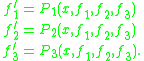
The name stems from the fact that the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
generated by the functions in such a chain is Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
.
Any Pfaffian chain is also a Noetherian chain; the extra variables in each polynomial are simply redundant in this case. But not every Noetherian chain is Pfaffian. If we take f1(x) = sin(x) and f2(x) = cos(x) then we have the equations
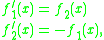
and these hold for all real numbers x, so f1,f2 is a Noetherian chain on all of R. But there is no polynomial P(x,y) such that the derivative of sin(x) can be written as P(x,sin(x)), and so this chain is not Pfaffian.

