Wiener deconvolution
Encyclopedia
.png)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Wiener deconvolution is an application of the Wiener filter
Wiener filter
In signal processing, the Wiener filter is a filter proposed by Norbert Wiener during the 1940s and published in 1949. Its purpose is to reduce the amount of noise present in a signal by comparison with an estimation of the desired noiseless signal. The discrete-time equivalent of Wiener's work was...
to the noise
Noise
In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...
problems inherent in deconvolution
Deconvolution
In mathematics, deconvolution is an algorithm-based process used to reverse the effects of convolution on recorded data. The concept of deconvolution is widely used in the techniques of signal processing and image processing...
. It works in the frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
, attempting to minimize the impact of deconvoluted noise at frequencies which have a poor signal-to-noise ratio
Signal-to-noise ratio
Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise...
.
The Wiener deconvolution method has widespread use in image
Image
An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:...
deconvolution applications, as the frequency spectrum of most visual images is fairly well behaved and may be estimated easily.
Wiener deconvolution is named after Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
.
Definition
Given a system: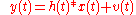
where
denotes convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
and:
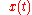is some input signal (unknown) at time 
.
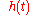is the known impulse responseImpulse responseIn signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
of a linear time-invariantLTI system theoryLinear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
system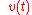
is some unknown additive noise, independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of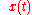
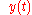is our observed signal
Our goal is to find some
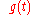so that we can estimate 
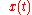as follows: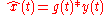
where
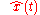is an estimate of 
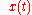that minimizes the mean square error.The Wiener deconvolution filter provides such a
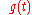. The filter is most easily described in the frequency domainFrequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
:
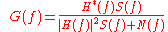
where:
-
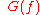and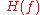 
are the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s of
and 
, respectively at frequency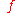 
. -
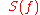is the mean power spectral density of the input signal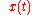 
-
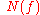is the mean power spectral density of the noise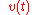 
- the superscript
denotes complex conjugationComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
.
The filtering operation may either be carried out in the time-domain, as above, or in the frequency domain:
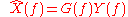
(where
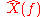is the Fourier transform of 
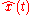) and then performing an inverse Fourier transform on 
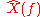to obtain 
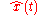.Note that in the case of images, the arguments
and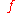 
above become two-dimensional; however the result is the same.Interpretation
The operation of the Wiener filter becomes apparent when the filter equation above is rewritten: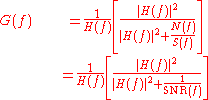
Here,
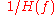is the inverse of the original system, and 
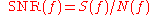is the signal-to-noise ratioSignal-to-noise ratio
Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise...
. When there is zero noise (i.e. infinite signal-to-noise), the term inside the square brackets equals 1, which means that the Wiener filter is simply the inverse of the system, as we might expect. However, as the noise at certain frequencies increases, the signal-to-noise ratio drops, so the term inside the square brackets also drops. This means that the Wiener filter attenuates frequencies dependent on their signal-to-noise ratio.
The Wiener filter equation above requires us to know the spectral content of a typical image, and also that of the noise. Often, we do not have access to these exact quantities, but we may be in a situation where good estimates can be made. For instance, in the case of photographic images, the signal (the original image) typically has strong low frequencies and weak high frequencies, and in many cases the noise content will be relatively flat with frequency.
Derivation
As mentioned above, we want to produce an estimate of the original signal that minimizes the mean square error, which may be expressed: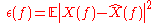
where
denotes expectationExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
.
If we substitute in the expression for
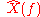, the above can be rearranged to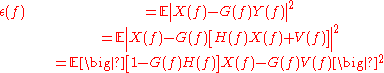
If we expand the quadratic, we get the following:
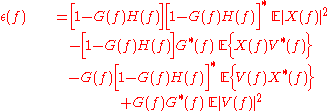
However, we are assuming that the noise is independent of the signal, therefore:
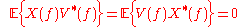
Also, we are defining the power spectral densities as follows:
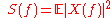
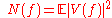
Therefore, we have:
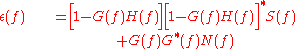
To find the minimum error value, we differentiate
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
with respect to
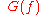and set equal to zero. As this is a complex value, 
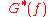acts as a constant.
This final equality can be rearranged to give the Wiener filter.
See also
- DeconvolutionDeconvolutionIn mathematics, deconvolution is an algorithm-based process used to reverse the effects of convolution on recorded data. The concept of deconvolution is widely used in the techniques of signal processing and image processing...
- Wiener filterWiener filterIn signal processing, the Wiener filter is a filter proposed by Norbert Wiener during the 1940s and published in 1949. Its purpose is to reduce the amount of noise present in a signal by comparison with an estimation of the desired noiseless signal. The discrete-time equivalent of Wiener's work was...
- Point spread functionPoint spread functionThe point spread function describes the response of an imaging system to a point source or point object. A more general term for the PSF is a system's impulse response, the PSF being the impulse response of a focused optical system. The PSF in many contexts can be thought of as the extended blob...
- Blind deconvolutionBlind deconvolutionIn image processing and applied mathematics, blind deconvolution is a deconvolution technique that permits recovery of the target scene from a single or set of "blurred" images in the presence of a poorly determined or unknown point spread function ....
- Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...