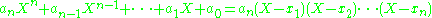Viète's formulas
Encyclopedia
In mathematics
, Vieta's formulas are formula
s that relate the coefficients of a polynomial
to sums and products of its roots. Named after François Viète
(more commonly referred to by the Latinised form of his name, Franciscus Vieta), the formulas are used specifically in algebra
.
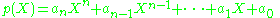
(with the coefficients being real or complex numbers and an ≠ 0) is known by the fundamental theorem of algebra
to have n (not necessarily distinct) complex roots x1, x2, ..., xn. Vieta's formulas relate the polynomial's coefficients { ak } to signed sums and products of its roots { xi } as follows:

Equivalently stated, the (n − k)th coefficient an−k is related to a signed sum of all possible subproducts of roots, taken k-at-a-time:
for k = 1, 2, ..., n (where we wrote the indices ik in increasing order to ensure each subproduct of roots is used exactly once).
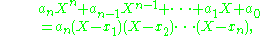
then Vieta's formulas even hold in any commutative ring
, and they merely express the way the coefficients on the left hand side are formed when expanding the product on the right. Note that the given relation has to be required even in the case of an integral domain, if one wishes to allow some of the roots to coincide, and therefore needs to specify what multiplicity should be associated to each root.
For the second degree polynomial (quadratic)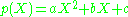 , roots
, roots 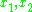 of the equation
of the equation 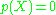 satisfy
satisfy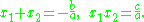
The first of these equations can be used to find the minimum (or maximum) of p. See second order polynomial.
For the cubic polynomial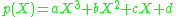 , roots
, roots 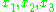 of the equation
of the equation 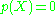 satisfy
satisfy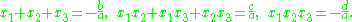
(which is true since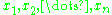 are all the roots of this polynomial), multiplying the factors on the right-hand side, and identifying the coefficients of each power of
are all the roots of this polynomial), multiplying the factors on the right-hand side, and identifying the coefficients of each power of 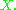
Formally, if one expands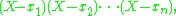 the terms are precisely
the terms are precisely 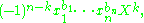 where
where 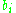 is either 0 or 1, accordingly as whether
is either 0 or 1, accordingly as whether 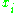 is included in the product or not, and k is the number of
is included in the product or not, and k is the number of 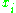 that are excluded, so the total number of factors in the product is n (counting
that are excluded, so the total number of factors in the product is n (counting 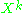 with multiplicity k) – as there are n binary choices (include
with multiplicity k) – as there are n binary choices (include  or X), there are
or X), there are  terms – geometrically, these can be understood as the vertices of a hypercube. Grouping these terms by degree yields the elementary symmetric polynomials in
terms – geometrically, these can be understood as the vertices of a hypercube. Grouping these terms by degree yields the elementary symmetric polynomials in 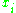 – for Xk, all distinct k-fold products of
– for Xk, all distinct k-fold products of 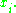
, for the case of positive roots.
In the opinion of the 18th century British mathematician Charles Hutton
, as quoted in , the general principle (not only for positive real roots) was first understood by the 17th century French mathematician Albert Girard
; Hutton writes:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Vieta's formulas are formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
s that relate the coefficients of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
to sums and products of its roots. Named after François Viète
François Viète
François Viète , Seigneur de la Bigotière, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to its innovative use of letters as parameters in equations...
(more commonly referred to by the Latinised form of his name, Franciscus Vieta), the formulas are used specifically in algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Basic formulas
Any general polynomial of degree n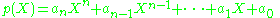
(with the coefficients being real or complex numbers and an ≠ 0) is known by the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
to have n (not necessarily distinct) complex roots x1, x2, ..., xn. Vieta's formulas relate the polynomial's coefficients { ak } to signed sums and products of its roots { xi } as follows:

Equivalently stated, the (n − k)th coefficient an−k is related to a signed sum of all possible subproducts of roots, taken k-at-a-time:
for k = 1, 2, ..., n (where we wrote the indices ik in increasing order to ensure each subproduct of roots is used exactly once).
Generalization to rings
Vieta's formulas hold more generally for polynomials with coefficients in any integral domain, as long as the leading coefficient an is invertible (so that the divisions make sense) and the polynomial has n distinct roots in that ring. The condition of being an integral domain is needed to assure that a polynomial of degree n cannot have more than n roots, and that if it has n roots then it is determined (up to a scalar) by those roots. However, if one replaces the assumption that x1, …, xn are the roots of the polynomial by the simpler requirement that one has the relation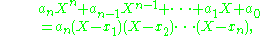
then Vieta's formulas even hold in any commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, and they merely express the way the coefficients on the left hand side are formed when expanding the product on the right. Note that the given relation has to be required even in the case of an integral domain, if one wishes to allow some of the roots to coincide, and therefore needs to specify what multiplicity should be associated to each root.
Example
Vieta's formulas applied to quadratic and cubic polynomial:For the second degree polynomial (quadratic)
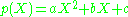 , roots
, roots 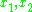 of the equation
of the equation 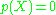 satisfy
satisfy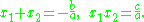
The first of these equations can be used to find the minimum (or maximum) of p. See second order polynomial.
For the cubic polynomial
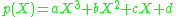 , roots
, roots 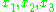 of the equation
of the equation 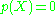 satisfy
satisfy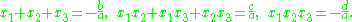
Proof
Vieta's formulas can be proved by expanding the equality(which is true since
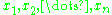 are all the roots of this polynomial), multiplying the factors on the right-hand side, and identifying the coefficients of each power of
are all the roots of this polynomial), multiplying the factors on the right-hand side, and identifying the coefficients of each power of 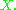
Formally, if one expands
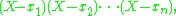 the terms are precisely
the terms are precisely 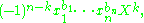 where
where 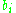 is either 0 or 1, accordingly as whether
is either 0 or 1, accordingly as whether 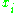 is included in the product or not, and k is the number of
is included in the product or not, and k is the number of 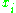 that are excluded, so the total number of factors in the product is n (counting
that are excluded, so the total number of factors in the product is n (counting 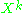 with multiplicity k) – as there are n binary choices (include
with multiplicity k) – as there are n binary choices (include  or X), there are
or X), there are  terms – geometrically, these can be understood as the vertices of a hypercube. Grouping these terms by degree yields the elementary symmetric polynomials in
terms – geometrically, these can be understood as the vertices of a hypercube. Grouping these terms by degree yields the elementary symmetric polynomials in 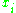 – for Xk, all distinct k-fold products of
– for Xk, all distinct k-fold products of 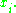
History
As reflected in the name, these formulas were discovered by the 16th century French mathematician François VièteFrançois Viète
François Viète , Seigneur de la Bigotière, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to its innovative use of letters as parameters in equations...
, for the case of positive roots.
In the opinion of the 18th century British mathematician Charles Hutton
Charles Hutton
Charles Hutton was an English mathematician.Hutton was born at Newcastle-on-Tyne. He was educated in a school at Jesmond, kept by Mr Ivison, a clergyman of the Church of England...
, as quoted in , the general principle (not only for positive real roots) was first understood by the 17th century French mathematician Albert Girard
Albert Girard
Albert Girard was a French-born mathematician. He studied at the University of Leiden. He "had early thoughts on the fundamental theorem of algebra" and gave the inductive definition for the Fibonacci numbers....
; Hutton writes:
...[Girard was] the first person who understood the general doctrine of the formation of the coefficients of the powers from the sum of the roots and their products. He was the first who discovered the rules for summing the powers of the roots of any equation.
See also
- Newton's identitiesNewton's identitiesIn mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
- Elementary symmetric polynomialElementary symmetric polynomialIn mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
- Symmetric polynomialSymmetric polynomialIn mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
- Content (algebra)Content (algebra)In algebra, the content of a polynomial is the highest common factor of its coefficients.A polynomial is primitive if it has content unity....
- Properties of polynomial roots
- Gauss–Lucas theorem
- Rational root theorem