Vitali convergence theorem
Encyclopedia
In mathematics
, the Vitali convergence theorem is a generalization of the better-known dominated convergence theorem
of Henri Lebesgue
. It is useful when a dominating function cannot be found for the sequence of functions in question; when such a dominating function can be found, Lebesgue's theorem follows as a special case of Vitali's. The result is named after the Italian
mathematician
Giuseppe Vitali
.
for each natural number
n ∈ N. Then fn converges as n → ∞ to another measurable function
f : X → R in Lp (i.e., in pth mean) if and only if
Strategy of proof when p = 1
When p = 1, a subsequence can be found so that
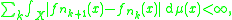
which implies that the subsequence converges in L1. The limit is necessarily equal to f. Arguing that this subsequence can be found as subsequence of any given subsequence shows that the whole sequence tends to f in L1-norm.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Vitali convergence theorem is a generalization of the better-known dominated convergence theorem
Dominated convergence theorem
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
of Henri Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
. It is useful when a dominating function cannot be found for the sequence of functions in question; when such a dominating function can be found, Lebesgue's theorem follows as a special case of Vitali's. The result is named after the Italian
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Giuseppe Vitali
Giuseppe Vitali
Giuseppe Vitali was an Italian mathematician who worked in several branches of mathematical analysis.- Mathematical contributions :...
.
Statement of the theorem
Let (X, Σ, μ) be a measure space; let p ≥ 1 and let fn : X → R belong to Lp(X, Σ, μ)Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for each natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n ∈ N. Then fn converges as n → ∞ to another measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
f : X → R in Lp (i.e., in pth mean) if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
- fn converges in measureConvergence in measureConvergence in measure can refer to two distinct mathematical concepts which both generalizethe concept of convergence in probability.-Definitions:...
to f;
- the |fn|p are uniformly integrable in the sense that,
- — for every ε > 0, there exists some t ≥ 0 such that, for all n ∈ N,
- — and, for every ε > 0, there exists some measurable set E ⊆ X with finite μ-measure such that, for all n ∈ N,
- (If X has finite μ-measure, then this third condition is always satisfied, since one can take E = X in every case.)
Strategy of proof when p = 1
When p = 1, a subsequence can be found so that
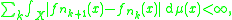
which implies that the subsequence converges in L1. The limit is necessarily equal to f. Arguing that this subsequence can be found as subsequence of any given subsequence shows that the whole sequence tends to f in L1-norm.