
Virial coefficient
Encyclopedia
Virial coefficients 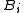 appear as coefficients in the virial expansion
appear as coefficients in the virial expansion
of the pressure of a many-particle system in powers of the density, providing systematic corrections to the ideal gas
law. They are characteristic of the interaction potential between the particles and in general depend on the temperature.
The second virial coefficient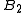 depends only on the pair interaction
depends only on the pair interaction
between the particles, the third ( ) depends on 2- and non-additive 3-body interactions, and so on.
) depends on 2- and non-additive 3-body interactions, and so on.
The first step in obtaining a closed expression for virial coefficients is a cluster expansion
of the grand canonical partition function
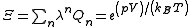
Here is the pressure,
is the pressure, 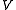 is the volume of the vessel containing the particles,
is the volume of the vessel containing the particles, 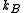 is Boltzmann's constant,
is Boltzmann's constant, 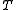 is the absolute
is the absolute
temperature,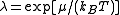 , with
, with 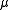 the chemical potential
the chemical potential
. The quantity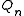 is the canonical partition
is the canonical partition
function of a subsystem of particles:
particles: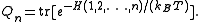
Here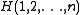 is the Hamiltonian (energy operator) of a subsystem of
is the Hamiltonian (energy operator) of a subsystem of
 particles. The Hamiltonian is a sum of the kinetic energies
particles. The Hamiltonian is a sum of the kinetic energies
of the particles
and the total -particle potential energy
-particle potential energy
(interaction energy). The latter includes pair interactions and possibly 3-body and higher-body interactions.
The grand partition function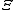 can be expanded in a sum of contributions from one-body, two-body, etc. clusters. The virial expansion is obtained from this expansion by observing that
can be expanded in a sum of contributions from one-body, two-body, etc. clusters. The virial expansion is obtained from this expansion by observing that 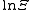 equals
equals 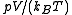 .
.
In this manner one derives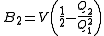
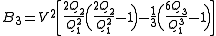 .
.
These are quantum-statistical expressions containing kinetic energies. Note that the one-particle partition function contains only a kinetic energy term. In the classical limit
contains only a kinetic energy term. In the classical limit
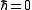 the kinetic energy operators commute with the potential operators and
the kinetic energy operators commute with the potential operators and
the kinetic energies in numerator and denominator cancel mutually. The trace (tr) becomes an integral over the configuration space. It follows that classical virial coefficients depend on the interactions between the particles only and are given as integrals over the particle coordinates.
The derivation of higher than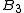 virial coefficients becomes quickly a complex
virial coefficients becomes quickly a complex
combinatorial problem. Making the classical approximation and
neglecting non-additive interactions (if present), the combinatorics
can be handled graphically as first shown by Joseph E. Mayer and Maria Goeppert-Mayer
.
They introduced what is now known as the Mayer function: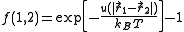
and wrote the cluster expansion in terms of these functions. Here
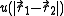
is the interaction between particle 1 and 2 (which are assumed to be identical particles).
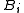 are related to the irreducible Mayer cluster integrals
are related to the irreducible Mayer cluster integrals 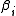 through
through
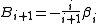
The latter are concisely defined in terms of graphs.

The rule for turning these graphs into integrals is as follows:
The first two cluster integrals are
In particular we get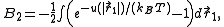
where particle 2 was assumed to define the origin (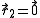 ).
).
This classical expression for the second virial coefficient was first derived by L. S.
Ornstein in his 1908 Leiden University Ph.D. thesis.
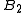 vanishes
vanishes
See further:
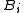 appear as coefficients in the virial expansion
appear as coefficients in the virial expansionVirial expansion
The classical virial expansion expresses the pressure of a many-particle system in equilibrium as a power series in the density.The virial expansion was introduced in 1901 by Heike Kamerlingh Onnesas a generalization of the ideal gas law...
of the pressure of a many-particle system in powers of the density, providing systematic corrections to the ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
law. They are characteristic of the interaction potential between the particles and in general depend on the temperature.
The second virial coefficient
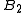 depends only on the pair interaction
depends only on the pair interactionbetween the particles, the third (
 ) depends on 2- and non-additive 3-body interactions, and so on.
) depends on 2- and non-additive 3-body interactions, and so on.The first step in obtaining a closed expression for virial coefficients is a cluster expansion
Cluster expansion
In statistical mechanics, the cluster expansion is a power series expansion of the partition function of a statistical field theory around a model that is a union of non-interacting 0-dimensional field theories. Cluster expansions originated in the work of...
of the grand canonical partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
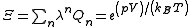
Here
 is the pressure,
is the pressure, 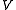 is the volume of the vessel containing the particles,
is the volume of the vessel containing the particles, 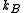 is Boltzmann's constant,
is Boltzmann's constant, 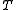 is the absolute
is the absolutetemperature,
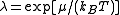 , with
, with 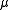 the chemical potential
the chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
. The quantity
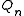 is the canonical partition
is the canonical partitionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
function of a subsystem of
 particles:
particles: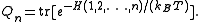
Here
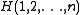 is the Hamiltonian (energy operator) of a subsystem of
is the Hamiltonian (energy operator) of a subsystem of particles. The Hamiltonian is a sum of the kinetic energies
particles. The Hamiltonian is a sum of the kinetic energiesKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the particles
and the total
 -particle potential energy
-particle potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
(interaction energy). The latter includes pair interactions and possibly 3-body and higher-body interactions.
The grand partition function
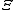 can be expanded in a sum of contributions from one-body, two-body, etc. clusters. The virial expansion is obtained from this expansion by observing that
can be expanded in a sum of contributions from one-body, two-body, etc. clusters. The virial expansion is obtained from this expansion by observing that 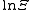 equals
equals 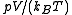 .
.In this manner one derives
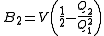
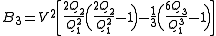 .
.These are quantum-statistical expressions containing kinetic energies. Note that the one-particle partition function
 contains only a kinetic energy term. In the classical limit
contains only a kinetic energy term. In the classical limit the kinetic energy operators commute with the potential operators and
the kinetic energy operators commute with the potential operators andthe kinetic energies in numerator and denominator cancel mutually. The trace (tr) becomes an integral over the configuration space. It follows that classical virial coefficients depend on the interactions between the particles only and are given as integrals over the particle coordinates.
The derivation of higher than
 virial coefficients becomes quickly a complex
virial coefficients becomes quickly a complexcombinatorial problem. Making the classical approximation and
neglecting non-additive interactions (if present), the combinatorics
can be handled graphically as first shown by Joseph E. Mayer and Maria Goeppert-Mayer
.
They introduced what is now known as the Mayer function:
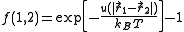
and wrote the cluster expansion in terms of these functions. Here
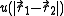
is the interaction between particle 1 and 2 (which are assumed to be identical particles).
Definition in terms of graphs
The virial coeffcients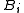 are related to the irreducible Mayer cluster integrals
are related to the irreducible Mayer cluster integrals 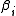 through
through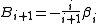
The latter are concisely defined in terms of graphs.

The rule for turning these graphs into integrals is as follows:
- Take a graph and label its white vertex by
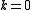 and the remaining black vertices with
and the remaining black vertices with  .
. - Associate a labelled coordinate k to each of the vertices, representing the continuous degrees of freedom associated with that particle. The coordinate 0 is reserved for the white vertex
- With each bond linking two vertices associate the Mayer f-functionMayer f-functionThe Mayer f-function is an auxiliary function that often appears in the series expansion of thermodynamic quantities related to classical many-particle systems.Donald Allan McQuarrie, Statistical Mechanics , page 228-Definition:...
corresponding to the interparticle potential - Integrate over all coordinates assigned to the black vertices
- Multiply the end result with the symmetry numberSymmetry numberThe symmetry number or symmetry order of an object is the number of different but indistinguishable arrangements of the object, i.e. the order of its symmetry group...
of the graph, defined as the inverse of the number of permutations of the black labelled vertices that leave the graph topologically invariant.
The first two cluster integrals are
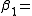 |
 |
|
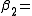 |
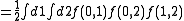 |
In particular we get
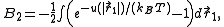
where particle 2 was assumed to define the origin (
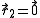 ).
).This classical expression for the second virial coefficient was first derived by L. S.
Ornstein in his 1908 Leiden University Ph.D. thesis.
See also
Boyle temperature - temperature at which the second virial coefficient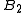 vanishes
vanishesLiterature
See further:
- J. P. Hansen and I. R. McDonald, The theory of Simple Liquids, Academic Press, London (1986).
- J. H. Dymond and E. B. Smith, The Virial Coefficients of Pure Gases and Mixtures: a Critical Compilation, Clarendon, Oxford (1980).

