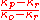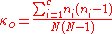Vigenère cipher
Encyclopedia
Encryption
In cryptography, encryption is the process of transforming information using an algorithm to make it unreadable to anyone except those possessing special knowledge, usually referred to as a key. The result of the process is encrypted information...
alphabet
Alphabet
An alphabet is a standard set of letters—basic written symbols or graphemes—each of which represents a phoneme in a spoken language, either as it exists now or as it was in the past. There are other systems, such as logographies, in which each character represents a word, morpheme, or semantic...
ic text by using a series of different Caesar cipher
Caesar cipher
In cryptography, a Caesar cipher, also known as a Caesar's cipher, the shift cipher, Caesar's code or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number...
s based on the letters of a keyword. It is a simple form of polyalphabetic substitution
Polyalphabetic cipher
A polyalphabetic cipher is any cipher based on substitution, using multiple substitution alphabets. The Vigenère cipher is probably the best-known example of a polyalphabetic cipher, though it is a simplified special case...
.
The Vigenère (viʒnɛːʁ) cipher has been reinvented many times. The method was originally described by Giovan Battista Bellaso
Giovan Battista Bellaso
-Biography:Bellaso was born of a distinguished family in 1505. His father was Piervincenzo, a patrician of Brescia, owner since the 15th century of a house in town and a suburban estate in Capriano, in a neighborhood called Fenili Belasi , including the Holy Trinity chapel. The chaplain was...
in his 1553 book La cifra del. Sig. Giovan Battista Bellaso; however, the scheme was later misattributed to Blaise de Vigenère
Blaise de Vigenère
Blaise de Vigenère was a French diplomat and cryptographer. The Vigenère cipher is so named due to the cipher being incorrectly attributed to him in the 19th century....
in the 19th century, and is now widely known as the "Vigenère cipher".
This cipher is well known because while it is easy to understand and implement, it often appears to beginners to be unbreakable; this earned it the description le chiffre indéchiffrable (French for 'the indecipherable cipher'). Consequently, many people have tried to implement encryption schemes that are essentially Vigenère ciphers, only to have them broken.
History
The first well documented description of a polyalphabetic cipher was formulated by Leon Battista Alberti around 1467 and used a metal cipher disc to switch between cipher alphabets. Alberti's system only switched alphabets after several words, and switches were indicated by writing the letter of the corresponding alphabet in the ciphertext. Later, in 1508, Johannes TrithemiusJohannes Trithemius
Johannes Trithemius , born Johann Heidenberg, was a German abbot, lexicographer, historian, cryptographer, polymath and occultist who had an influence on later occultism. The name by which he is more commonly known is derived from his native town of Trittenheim on the Mosel in Germany.-Life:He...
, in his work Poligraphia, invented the tabula recta
Tabula recta
In cryptography, the tabula recta is a square table of alphabets, each row of which is made by shifting the previous one to the left...
, a critical component of the Vigenère cipher. The Trithemius cipher
Trithemius cipher
The Trithemius cipher is a polyalphabetic cipher invented by the German author and monk Johannes Trithemius in the 15th century. The cipher was published in his book Polygraphia, which is credited with being the first published work on cryptology. It uses a letter square with the 26 letters of the...
, however, only provided a progressive, rigid and predictable system for switching between cipher alphabets.
What is now known as the Vigenère cipher was originally described by Giovan Battista Bellaso
Giovan Battista Bellaso
-Biography:Bellaso was born of a distinguished family in 1505. His father was Piervincenzo, a patrician of Brescia, owner since the 15th century of a house in town and a suburban estate in Capriano, in a neighborhood called Fenili Belasi , including the Holy Trinity chapel. The chaplain was...
in his 1553 book La cifra del. Sig. Giovan Battista Bellaso. He built upon the tabula recta of Trithemius, but added a repeating "countersign" (a key
Key (cryptography)
In cryptography, a key is a piece of information that determines the functional output of a cryptographic algorithm or cipher. Without a key, the algorithm would produce no useful result. In encryption, a key specifies the particular transformation of plaintext into ciphertext, or vice versa...
) to switch cipher alphabets every letter. Whereas Alberti and Trithemius used a fixed pattern of substitutions, Bellaso's scheme meant the pattern of substitutions could be easy changed simply by selecting a new key. Keys were typically single words or short phrases, known to both parties in advance, or transmitted "out of band" along with the message. Bellaso's method thus required strong security for only the key. As it is relatively easy to secure a short key phrase, say by a previous private conversation, Bellaso's system was considerably more secure.
Blaise de Vigenère
Blaise de Vigenère
Blaise de Vigenère was a French diplomat and cryptographer. The Vigenère cipher is so named due to the cipher being incorrectly attributed to him in the 19th century....
published his description of a similar but stronger autokey cipher
Autokey cipher
An autokey cipher is a cipher which incorporates the message into the key. There are two forms of autokey cipher: key autokey and text autokey ciphers. A key-autokey cipher uses previous members of the keystream to determine the next element in the keystream...
before the court of Henry III of France
Henry III of France
Henry III was King of France from 1574 to 1589. As Henry of Valois, he was the first elected monarch of the Polish-Lithuanian Commonwealth with the dual titles of King of Poland and Grand Duke of Lithuania from 1573 to 1575.-Childhood:Henry was born at the Royal Château de Fontainebleau,...
, in 1586. Later, in the 19th century, the invention of Bellaso's cipher was misattributed to Vigenère. David Kahn in his book The Codebreakers lamented the misattribution by saying that history had "ignored this important contribution and instead named a regressive and elementary cipher for him [Vigenère] though he had nothing to do with it".
The Vigenère cipher gained a reputation for being exceptionally strong. Noted author and mathematician Charles Lutwidge Dodgson (Lewis Carroll
Lewis Carroll
Charles Lutwidge Dodgson , better known by the pseudonym Lewis Carroll , was an English author, mathematician, logician, Anglican deacon and photographer. His most famous writings are Alice's Adventures in Wonderland and its sequel Through the Looking-Glass, as well as the poems "The Hunting of the...
) called the Vigenère cipher unbreakable in his 1868 piece "The Alphabet Cipher
The Alphabet Cipher
Lewis Carroll published The Alphabet-Cipher in 1868, possibly in a children's magazine. It describes what is known as a Vigenère cipher, a well-known scheme in cryptography...
" in a children's magazine. In 1917, Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
described the Vigenère cipher as "impossible of translation". This reputation was not deserved. Charles Babbage
Charles Babbage
Charles Babbage, FRS was an English mathematician, philosopher, inventor and mechanical engineer who originated the concept of a programmable computer...
was known to have broken a variant of the cipher as early as 1854; however, he didn't publish his work. Kasiski entirely broke the cipher and published the technique in the 19th century. Even before this, though, some skilled cryptanalysts could occasionally break the cipher in the 16th century.
The Vigenère cipher is simple enough to be a field cipher if it is used in conjunction with cipher disks. The Confederate States of America
Confederate States of America
The Confederate States of America was a government set up from 1861 to 1865 by 11 Southern slave states of the United States of America that had declared their secession from the U.S...
, for example, used a brass cipher disk to implement the Vigenère cipher during the American Civil War
American Civil War
The American Civil War was a civil war fought in the United States of America. In response to the election of Abraham Lincoln as President of the United States, 11 southern slave states declared their secession from the United States and formed the Confederate States of America ; the other 25...
. The Confederacy's messages were far from secret and the Union regularly cracked their messages. Throughout the war, the Confederate leadership primarily relied upon three key phrases, "Manchester Bluff", "Complete Victory" and, as the war came to a close, "Come Retribution".
Gilbert Vernam
Gilbert Vernam
Gilbert Sandford Vernam was an AT&T Bell Labs engineer who, in 1917, invented the stream cipher and later co-invented the one-time pad cipher. Vernam proposed a teleprinter cipher in which a previously-prepared key, kept on paper tape, is combined character by character with the plaintext message...
tried to repair the broken cipher (creating the Vernam-Vigenère cipher in 1918), but, no matter what he did, the cipher was still vulnerable to cryptanalysis. Vernam's work, however, eventually led to the one-time pad
One-time pad
In cryptography, the one-time pad is a type of encryption, which has been proven to be impossible to crack if used correctly. Each bit or character from the plaintext is encrypted by a modular addition with a bit or character from a secret random key of the same length as the plaintext, resulting...
, a provably unbreakable cipher.
Description
In a Caesar cipherCaesar cipher
In cryptography, a Caesar cipher, also known as a Caesar's cipher, the shift cipher, Caesar's code or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number...
, each letter of the alphabet is shifted along some number of places; for example, in a Caesar cipher of shift 3, A would become D, B would become E, Y would become B and so on. The Vigenère cipher consists of several Caesar ciphers in sequence with different shift values.
To encrypt, a table of alphabets can be used, termed a tabula recta
Tabula recta
In cryptography, the tabula recta is a square table of alphabets, each row of which is made by shifting the previous one to the left...
, Vigenère square, or Vigenère table. It consists of the alphabet written out 26 times in different rows, each alphabet shifted cyclically to the left compared to the previous alphabet, corresponding to the 26 possible Caesar ciphers. At different points in the encryption process, the cipher uses a different alphabet from one of the rows. The alphabet used at each point depends on a repeating keyword.
For example, suppose that the plaintext
Plaintext
In cryptography, plaintext is information a sender wishes to transmit to a receiver. Cleartext is often used as a synonym. Before the computer era, plaintext most commonly meant message text in the language of the communicating parties....
to be encrypted is:
- attackatdawn
The person sending the message chooses a keyword and repeats it until it matches the length of the plaintext, for example, the keyword "LEMON":
- LEMONLEMONLE
Each row starts with a key letter. The remainder of the row holds the letters A to Z (in shifted order). Although there are 26 key rows shown, you will only use as many keys (different alphabets) as there are unique letters in the key string, here just 5 keys, {L, E, M, O, N}. For successive letters of the message, we are going to take successive letters of the key string, and encipher each message letter using its corresponding key row. Choose the next letter of the key, go along that row to find the column heading that matches the message character; the letter at the intersection of [key-row, msg-col] is the enciphered letter.
For example, the first letter of the plaintext, A, is paired with L, the first letter of the key. So use row L and column A of the Vigenère square, namely L. Similarly, for the second letter of the plaintext, the second letter of the key is used; the letter at row E and column T is X. The rest of the plaintext is enciphered in a similar fashion:
| Plaintext: | attackatdawn |
| Key: | LEMONLEMONLE |
| Ciphertext: | LXFOPVEFRNHR |
Decryption is performed by going to the row in the table corresponding to the key, finding the position of the ciphertext letter in this row, and then using the column's label as the plaintext. For example, in row L (from LEMON), the ciphertext L appears in column A, which is the first plaintext letter. Next we go to row E (from LEMON), locate the ciphertext X which is found in column T, thus T is the second plaintext letter.
Algebraic description
Vigenère can also be viewed algebraically. If the letters A–Z are taken to be the numbers 0–25, and addition is performed moduloModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
26, then Vigenère encryption
using the key 
can be written,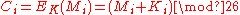
and decryption
using the key 
,
,whereas
is the message, 
is the ciphertext and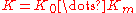 
is the used key.Thus using the previous example, to encrypt
with key letter 
the calculation would result in 
.
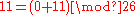
Therefore to decrypt
with key letter 
the calculation would result in 
.
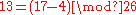
Cryptanalysis
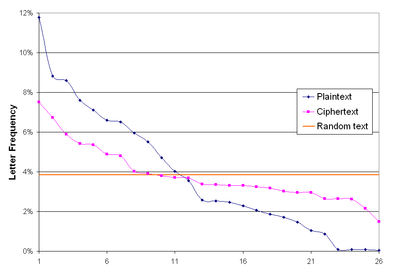
Letter frequencies
The frequency of letters in text has often been studied for use in cryptography, and frequency analysis in particular. No exact letter frequency distribution underlies a given language, since all writers write slightly differently. Linotype machines sorted the letters' frequencies as etaoin shrdlu...
, which interferes with a straightforward application of frequency analysis
Frequency analysis
In cryptanalysis, frequency analysis is the study of the frequency of letters or groups of letters in a ciphertext. The method is used as an aid to breaking classical ciphers....
. For instance, if P is the most frequent letter in a ciphertext whose plaintext is in English
English language
English is a West Germanic language that arose in the Anglo-Saxon kingdoms of England and spread into what was to become south-east Scotland under the influence of the Anglian medieval kingdom of Northumbria...
, one might suspect that P corresponds to E, because E is the most frequently used letter in English. However, using the Vigenère cipher, E can be enciphered as different ciphertext letters at different points in the message, thus defeating simple frequency analysis.
The primary weakness of the Vigenère cipher is the repeating nature of its key
Key (cryptography)
In cryptography, a key is a piece of information that determines the functional output of a cryptographic algorithm or cipher. Without a key, the algorithm would produce no useful result. In encryption, a key specifies the particular transformation of plaintext into ciphertext, or vice versa...
. If a cryptanalyst correctly guesses the key's length, then the cipher text can be treated as interwoven Caesar cipher
Caesar cipher
In cryptography, a Caesar cipher, also known as a Caesar's cipher, the shift cipher, Caesar's code or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number...
s, which individually are easily broken. The Kasiski and Friedman tests can help determine the key length.
Kasiski examination
- For more details on this topic, see Kasiski examinationKasiski examinationIn cryptanalysis, Kasiski examination is a method of attacking polyalphabetic substitution ciphers, such as the Vigenère cipher...
.
In 1863 Friedrich Kasiski
Friedrich Kasiski
Major Friedrich Wilhelm Kasiski was a Prussian infantry officer, cryptographer and archeologist. Kasiski was born in Schlochau, West Prussia .-Military service:...
was the first to publish a successful general attack on the Vigenère cipher. Earlier attacks relied on knowledge of the plaintext, or use of a recognizable word as a key. Kasiski's method had no such dependencies. Kasiski was the first to publish an account of the attack, but it's clear that there were others who were aware of it. In 1854, Charles Babbage
Charles Babbage
Charles Babbage, FRS was an English mathematician, philosopher, inventor and mechanical engineer who originated the concept of a programmable computer...
was goaded into breaking the Vigenère cipher when John Hall Brock Thwaites submitted a "new" cipher to the Journal of the Society of the Arts. When Babbage showed that Thwaites' cipher was essentially just another recreation of the Vigenère cipher, Thwaites challenged Babbage to break his cipher encoded twice, with keys of different length. Babbage succeeded in decrypting a sample, which turned out to be the poem "The Vision of Sin", by Alfred Tennyson, encrypted according to the keyword "Emily", the first name of Tennyson's wife. Babbage never explained the method he used. Studies of Babbage's notes reveal that he had used the method later published by Kasiski, and suggest that he had been using the method as early as 1846.
The Kasiski examination
Kasiski examination
In cryptanalysis, Kasiski examination is a method of attacking polyalphabetic substitution ciphers, such as the Vigenère cipher...
, also called the Kasiski test, takes advantage of the fact that repeated words may, by chance, sometimes be encrypted using the same key letters, leading to repeated groups in the ciphertext. For example, Consider the following encryption using the keyword ABCD:
Key: ABCDABCDABCDABCDABCDABCDABCD
Plaintext: CRYPTOISSHORTFORCRYPTOGRAPHY
Ciphertext: CSASTPKVSIQUTGQUCSASTPIUAQJB
There is an easily seen repetition in the ciphertext, and the Kasiski test will be effective.
Here the distance between the repetitions of CSASTP is 16. Assuming that the repeated segments represent the same plaintext segments, this implies that the key is 16, 8, 4, 2, or 1 characters long. (All factors
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
of the distance are possible key lengths – a key of length one is just a simple shift cipher, where cryptanalysis is much easier.) Since key lengths 2 and 1 are unrealistically short, one only needs to try lengths 16, 8, or 4. Longer messages make the test more accurate because they usually contain more repeated ciphertext segments. The following ciphertext has two segments that are repeated:
Ciphertext: VHVSSPQUCEMRVBVBBBVHVSURQGIBDUGRNICJQUCERVUAXSSR
The distance between the repetitions of VHVS is 18. Assuming that the repeated segments represent the same plaintext segments, this implies that the key is 18, 9, 6, 3, 2, or 1 characters long. The distance between the repetitions of QUCE is 30 characters. This means that the key length could be 30, 15, 10, 6, 5, 3, 2, or 1 characters long. By taking the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of these sets one could safely conclude that the most likely key length is 6, since 3, 2, and 1 are unrealistically short.
Friedman test
The Friedman test (sometimes known as the kappa test) was invented during the 1920s by William F. FriedmanWilliam F. Friedman
William Frederick Friedman was a US Army cryptographer who ran the research division of the Army's Signals Intelligence Service in the 1930s, and parts of its follow-on services into the 1950s...
. Friedman used the index of coincidence
Index of coincidence
In cryptography, coincidence counting is the technique of putting two texts side-by-side and counting the number of times that identical letters appear in the same position in both texts...
, which measures the unevenness of the cipher letter frequencies to break the cipher. By knowing the probability
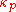that any two randomly chosen source-language letters are the same (around 0.067 for monocase English) and the probability of a coincidence for a uniform random selection from the alphabet 
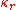(1/26 = 0.0385 for English), the key length can be estimated as:
from the observed coincidence rate
where c is the size of the alphabet (26 for English), N is the length of the text, and n1 through nc are the observed ciphertext letter frequencies
Letter frequencies
The frequency of letters in text has often been studied for use in cryptography, and frequency analysis in particular. No exact letter frequency distribution underlies a given language, since all writers write slightly differently. Linotype machines sorted the letters' frequencies as etaoin shrdlu...
, as integers.
This is, however, only an approximation whose accuracy increases with the size of the text. It would in practice be necessary to try various key lengths close to the estimate. A better approach for repeating-key ciphers is to copy the ciphertext into rows of a matrix having as many columns as an assumed key length, then compute the average index of coincidence with each column considered separately; when this is done for each possible key length, the highest average I.C. then corresponds to the most likely key length. Such tests may be supplemented by information from the Kasiski examination.
Frequency analysis
Once the length of the key is known, the ciphertext can be rewritten into that many columns, with each column corresponding to a single letter of the key. Each column consists of plaintext that has been encrypted by a single Caesar cipherCaesar cipher
In cryptography, a Caesar cipher, also known as a Caesar's cipher, the shift cipher, Caesar's code or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number...
; the Caesar key (shift) is just the letter of the Vigenère key that was used for that column. Using methods similar to those used to break the Caesar cipher, the letters in the ciphertext can be discovered.
An improvement to the Kasiski examination, known as Kerckhoffs
Auguste Kerckhoffs
Auguste Kerckhoffs was a Dutch linguist and cryptographer who was professor of languages at the École des Hautes Études Commerciales in Paris in the late 19th century....
' method, matches each column's letter frequencies to shifted plaintext frequencies to discover the key letter (Caesar shift) for that column. Once every letter in the key is known, the cryptanalyst can simply decrypt the ciphertext and reveal the plaintext. Kerckhoffs' method is not applicable when the Vigenère table has been scrambled, rather than using normal alphabetic sequences, although Kasiski examination and coincidence tests can still be used to determine key length in that case.
Key elimination
The Vigenère cipher function is essentially modulo arithmetic, and thus commutative. So if the key length is known (or guessed) then subtracting the cipher text from itself, offset by the key length will produce the cipher text encrypted with itself. If any words in the cipher text are known or can be guessed, then the plain text and also the key, will be revealed. This is useful if the key is an obscure sequence of letters because the plain text will generally be ordinary words.Key elimination is useful for making short versions of the plain text.
Variants
The running keyRunning key cipher
In classical cryptography, the running key cipher is a type of polyalphabetic substitution cipher in which a text, typically from a book, is used to provide a very long keystream...
variant of the Vigenère cipher was also considered unbreakable at one time. This version uses as the key a block of text as long as the plaintext. Since the key is as long as the message the Friedman and Kasiski tests no longer work (the key is not repeated). In 1920, Friedman was the first to discover this variant's weaknesses. The problem with the running key Vigenère cipher is that the cryptanalyst has statistical information about the key (assuming that the block of text is in a known language) and that information will be reflected in the ciphertext.
If using a key which is truly random, is at least as long as the encrypted message and is used only once, the Vigenère cipher is theoretically unbreakable. However, in this case it is the key, not the cipher, which provides cryptographic strength and such systems are properly referred to collectively as one-time pad
One-time pad
In cryptography, the one-time pad is a type of encryption, which has been proven to be impossible to crack if used correctly. Each bit or character from the plaintext is encrypted by a modular addition with a bit or character from a secret random key of the same length as the plaintext, resulting...
systems, irrespective of which ciphers are employed.
Vigenère actually invented a stronger cipher: an autokey cipher
Autokey cipher
An autokey cipher is a cipher which incorporates the message into the key. There are two forms of autokey cipher: key autokey and text autokey ciphers. A key-autokey cipher uses previous members of the keystream to determine the next element in the keystream...
. The name "Vigenère cipher" became associated with a simpler polyalphabetic cipher instead. In fact, the two ciphers were often confused, and both were sometimes called "le chiffre indéchiffrable". Babbage actually broke the much stronger autokey cipher, while Kasiski is generally credited with the first published solution to the fixed-key polyalphabetic ciphers.
A simple variant is to encrypt using the Vigenère decryption method, and decrypt using Vigenère encryption. This method is sometimes referred to as "Variant Beaufort". This is different from the Beaufort cipher
Beaufort cipher
The Beaufort cipher, created by Sir Francis Beaufort, is a substitution cipher that is similar to the Vigenère cipher but uses a slightly modified enciphering mechanism and tableau....
, created by Sir Francis Beaufort
Francis Beaufort
Rear-Admiral Sir Francis Beaufort, FRS, FRGS was an Irish hydrographer and officer in Britain's Royal Navy...
, which nonetheless is similar to Vigenère but uses a slightly modified enciphering mechanism and tableau. The Beaufort cipher is a reciprocal cipher
Reciprocal cipher
A reciprocal cipher means, just as one enters the plaintext into the cryptography system to get the ciphertext, one could enter the ciphertext into the same place in the system to get the plaintext. Sometimes also referred as self-reciprocal cipher....
.
Despite the Vigenère cipher's apparent strength it never became widely used throughout Europe
Europe
Europe is, by convention, one of the world's seven continents. Comprising the westernmost peninsula of Eurasia, Europe is generally 'divided' from Asia to its east by the watershed divides of the Ural and Caucasus Mountains, the Ural River, the Caspian and Black Seas, and the waterways connecting...
. The Gronsfeld
Gronsveld
Gronsveld is a village in the Dutch province of Limburg. It is part of the municipality of Eijsden and situated southeast of the municipality of Maastricht, to which it is bordering....
cipher is a variant created by Count Gronsfeld which is identical to the Vigenère cipher, except that it uses just 10 different cipher alphabets (corresponding to the digits 0 to 9). The Gronsfeld cipher is strengthened because its key is not a word, but it is weakened because it has just 10 cipher alphabets. Gronsfeld's cipher did become widely used throughout Germany and Europe, despite its weaknesses.
Sources
- Mendelsohn, Charles J. (1940). "Blaise De Vigenere and The "Chiffre Carre"," Proceedings of the American Philosophical Society 82, no. 2
Articles
- History of the cipher from Cryptologia
- Basic Cryptanalysis at H2G2
- Lecture Notes on Classical Cryptology including an explanation and derivation of the Friedman Test
- Online Vigenère Cracking Tool
- Civil War vigenère cipher cracked in 2010
Programming
- Sharky's Online Vigenere Cipher — Encode and decode messages, using a known key, within a Web browser (JavaScriptJavaScriptJavaScript is a prototype-based scripting language that is dynamic, weakly typed and has first-class functions. It is a multi-paradigm language, supporting object-oriented, imperative, and functional programming styles....
) - PyGenere: an online tool for automatically deciphering Vigenère-encoded texts (6 languages supported)
- Vigenère Cipher encryption and decryption program (browser version, English only)
- Crypt::Vigenere — a CPANCPANCPAN, the Comprehensive Perl Archive Network, is an archive of nearly 100,000 modules of software written in Perl, as well as documentation for it. It has a presence on the World Wide Web at and is mirrored worldwide at more than 200 locations...
module implementing the Vigenère cipher - Breaking the indecipherable cipher: Perl code to decipher Vigenère text, with the source in the shape of Babbage's head
- Random Vigenère Challenges
- Vigenère in BASH
- Vigenère Cipher - Source code in Java (GNU GPLv3GNU General Public LicenseThe GNU General Public License is the most widely used free software license, originally written by Richard Stallman for the GNU Project....
) - Java Vigenere applet with source code (GNU GPLGNU General Public LicenseThe GNU General Public License is the most widely used free software license, originally written by Richard Stallman for the GNU Project....
) - Vigenere Cipher in Java
- Vijner 974 Encryption Tool in C# (Vigenere Algorithm)