Vicsek fractal
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Vicsek fractal, also known as Vicsek snowflake or box fractal, is a fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
arising from a construction similar to that of the Sierpinski carpet
Sierpinski carpet
The Sierpinski carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is a generalization of the Cantor set to two dimensions . Sierpiński demonstrated that this fractal is a universal curve, in that any possible one-dimensional graph, projected onto the two-dimensional...
. It has applications including as compact antennas
Fractal antenna
A fractal antenna is an antenna that uses a fractal, self-similar design to maximize the length, or increase the perimeter , of material that can receive or transmit electromagnetic radiation within a given total surface area or volume.Such fractal antennas are also referred to as multilevel and...
, particularly in cellular phones.
Construction
The basic square is decomposed into nine smaller squares in the 3-by-3 grid. The four squares at the corners and the middle square are left, the other squares being removed. The process is repeated recursively for each of the five remaining subsquares. The Vicsek fractal is the set obtained at the limit of this procedure. The Hausdorff dimensionHausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
of this fractal is
≈ 1.46497.An alternative construction (shown below in the left image) is to remove the four corner squares and leave the middle square and the squares above, below, left and right of it. The two constructions produce identical limiting curves, but one is rotated by 45 degrees with respect to the other.
Properties
The Vicsek fractal has the surprising property that it has zero area yet an infinite perimeterPerimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
, due to its non-integer dimension. At each iteration, four squares are removed for every five retained, meaning that at iteration n the area is
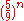(assuming an initial square of side length 1). When n approached infinity, the area approaches zero. The perimeter however is 
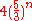, because each side is divided into three parts and the center one is replaced with three sides, yielding an increase of three to five. The perimeter approaches infinity as n increases.The boundary of the Vicsek fractal is the Type 1 quadratic Koch curve.
Analogues in higher dimensions
There is a three-dimensional analogue of the Vicsek fractal. It is constructed by subdividing each cube into 27 smaller ones, and removing all but the "center cross", the central cube and the six cubes touching the center of each face. Its Hausdorff dimension is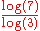
≈ 1.7712.Similarly to the two-dimensional Vicsek fractal, this figure has zero volume. Each iteration removes retains 7 cubes for every 27, meaning a volume of
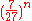at iteration n, which approaches zero as n approaches infinity.There exist an inifinite number of cross section
Cross section (geometry)
In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...
s which yield the two-dimensional Vicsek fractal.
See also
- Cross crosslet
- List of fractals by Hausdorff dimension
- Sierpinski carpetSierpinski carpetThe Sierpinski carpet is a plane fractal first described by Wacław Sierpiński in 1916. The carpet is a generalization of the Cantor set to two dimensions . Sierpiński demonstrated that this fractal is a universal curve, in that any possible one-dimensional graph, projected onto the two-dimensional...
- Sierpinski triangleSierpinski triangleThe Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
- N-flakeN-flakeAn n-flake, polyflake, or Sierpinski n-gon, is a fractal constructed starting from an n-gon. This n-gon is replaced by a flake of smaller n-gons, such that the scaled polygons are placed at the vertices, and sometimes in the center. This process is repeated recursively to result in the fractal...