N-flake
Encyclopedia
An n-flake, polyflake, or Sierpinski n-gon, is a fractal
constructed starting from an n-gon. This n-gon is replaced by a flake of smaller n-gons, such that the scaled polygons are placed at the vertices
, and sometimes in the center. This process is repeated recursively to result in the fractal. Typically, there is also the restriction that the n-gons must touch yet not overlap.
The formula of the scale factor
r for any n-flake is: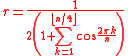
where cosine is evaluated in radians and n is the number of sides of the n-gon. The Hausdorff dimension
of a n-flake is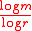
, where m is the number of polygons in each individual flake and r is the scale factor.
is an n-flake formed by successive flakes of three triangles. Each flake is formed by placing triangles scaled by 1/2 in each corner of the triangle they replace. Its Hausdorff dimension
is equal to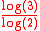
≈ 1.585. The 
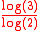is obtained because each iteration has 3 triangles that are scaled by 1/2.
, rarely called a quadraflake, is formed by successive flakes of five squares scaled by 1/3. Each flake is formed either by placing a scaled square in each corner and one in the center or one on each side of the square and one in the center. Its Hausdorff dimension is equal to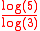
≈ 1.4650. The 
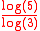is obtained because each iteration has 5 squares that are scaled by 1/3. The boundary of the Vicsek Fractal is a Type 1 quadratic Koch curve.
Each flake is formed by placing a pentagon in each corner and one in the center. Its Hausdorff dimension is equal to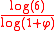
≈ 1.8617, where 
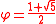(golden ratio
). The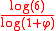
is obtained because each iteration has 6 pentagons that are scaled by 
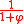. The boundary of a pentaflake is the Koch curve of 72 degrees.
There is also a variation of the pentaflake that has no central pentagon. Its Hausdorff dimension equals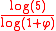
≈ 1.6723. This variation still contains infinitely many Koch curves, but they are somewhat more visible.
, or sierpinski hexagon, is formed by successive flakes of seven regular hexagons. Each flake is formed by placing a scaled hexagon in each corner and one in the center. Its Hausdorff dimension is equal to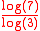
≈ 1.7712. The 
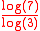is obtained because each iteration has 7 hexagons that are scaled by 1/3. The boundary of a hexaflake is the standard Koch curve of 60 degrees and infinitely many Koch snowflake
s are contained within. Also, the projection of the cantor cube onto the plane orthogonal to its main diagonal is a hexaflake.
Like the pentaflake, there is also a variation of the hexaflake that has no central hexagon. Its Hausdorff dimension equals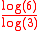
≈ 1.6309. This variation still contains infinitely many Koch curves of 60 degrees.
.
scaled by 1/2 in each corner. Its Hausdorff dimension is equal to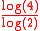
, which is exactly equal to 2. On every face there is a Sierpinski triangle and infinitely many are contained within.
, where every cube is replaced by a three dimensional ring of cubes. Its Hausdorff dimension is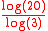
≈ 2.7268.
Another hexahedron flake can be produced in a manner similar to the Vicsek fractal
extended to three dimensions. Every cube is divided into 27 smaller cubes and the center cross is retained, which is the opposite of the Menger sponge
where the cross is removed. However, it is not the Menger Sponge complement. Its Hausdorff dimension is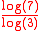
≈ 1.7712, because a cross of 7 cubes, each scaled by 1/3, replaces each cube.
scaled by 1/2 in each corner. Its Hausdorff dimension is equal to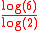
≈ 2.5849. On every face there is a Sierpinski triangle and infinitely many are contained within.
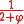in each corner. Its Hausdorff dimension is equal to 
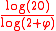≈ 2.3296.
scaled by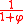
in each corner. Its Hausdorff dimension is equal to 
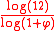≈ 2.5819.
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
constructed starting from an n-gon. This n-gon is replaced by a flake of smaller n-gons, such that the scaled polygons are placed at the vertices
Vertex
Vertex may refer to:-Mathematics:*Vertex , an angle point of any shape or angle*Vertex , a node in a graph*Vertex , a local extreme point of curvature...
, and sometimes in the center. This process is repeated recursively to result in the fractal. Typically, there is also the restriction that the n-gons must touch yet not overlap.
In two dimensions
The most common variety of n-flake is two-dimensional (in terms of its topological dimension) and is formed of polygons. The four most common special cases are formed with triangles, squares, pentagons, and hexagons, but it can be extended to any polygon. Its boundary is the von Koch curve of varying types – depending on the n-gon – and infinitely many Koch curves are contained within. The fractals occupy zero area yet have an infinite perimeter.The formula of the scale factor
Scale factor
A scale factor is a number which scales, or multiplies, some quantity. In the equation y=Cx, C is the scale factor for x. C is also the coefficient of x, and may be called the constant of proportionality of y to x...
r for any n-flake is:
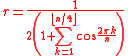
where cosine is evaluated in radians and n is the number of sides of the n-gon. The Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
of a n-flake is
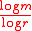, where m is the number of polygons in each individual flake and r is the scale factor.Sierpinski triangle
The Sierpinski triangleSierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
is an n-flake formed by successive flakes of three triangles. Each flake is formed by placing triangles scaled by 1/2 in each corner of the triangle they replace. Its Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
is equal to
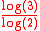≈ 1.585. The 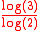is obtained because each iteration has 3 triangles that are scaled by 1/2.Vicsek fractal
If a sierpinski 4-gon were constructed from the given definition, the scale factor would be 1/2 and the fractal would simply be a square. A more interesting alternative, the Vicsek fractalVicsek fractal
In mathematics the Vicsek fractal, also known as Vicsek snowflake or box fractal, is a fractal arising from a construction similar to that of the Sierpinski carpet. It has applications including as compact antennas, particularly in cellular phones....
, rarely called a quadraflake, is formed by successive flakes of five squares scaled by 1/3. Each flake is formed either by placing a scaled square in each corner and one in the center or one on each side of the square and one in the center. Its Hausdorff dimension is equal to
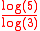≈ 1.4650. The 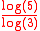is obtained because each iteration has 5 squares that are scaled by 1/3. The boundary of the Vicsek Fractal is a Type 1 quadratic Koch curve.Pentaflake
A pentaflake, or sierpinski pentagon, is formed by successive flakes of six regular pentagons.Each flake is formed by placing a pentagon in each corner and one in the center. Its Hausdorff dimension is equal to
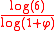≈ 1.8617, where 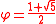(golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
). The
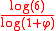is obtained because each iteration has 6 pentagons that are scaled by 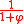. The boundary of a pentaflake is the Koch curve of 72 degrees.There is also a variation of the pentaflake that has no central pentagon. Its Hausdorff dimension equals
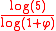≈ 1.6723. This variation still contains infinitely many Koch curves, but they are somewhat more visible.Hexaflake
A hexaflakeHexaflake
A hexaflake is a fractal constructed by iteratively exchanging each hexagon by a flake of seven hexagons; it is a special case of the n-flake. As such, a hexaflake would have 7n-1 hexagons in its nth iteration. Its boundary is the von Koch flake, and contains an infinite number of Koch snowflakes...
, or sierpinski hexagon, is formed by successive flakes of seven regular hexagons. Each flake is formed by placing a scaled hexagon in each corner and one in the center. Its Hausdorff dimension is equal to
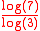≈ 1.7712. The 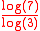is obtained because each iteration has 7 hexagons that are scaled by 1/3. The boundary of a hexaflake is the standard Koch curve of 60 degrees and infinitely many Koch snowflakeKoch snowflake
The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
s are contained within. Also, the projection of the cantor cube onto the plane orthogonal to its main diagonal is a hexaflake.
Like the pentaflake, there is also a variation of the hexaflake that has no central hexagon. Its Hausdorff dimension equals
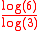≈ 1.6309. This variation still contains infinitely many Koch curves of 60 degrees.Polyflake
n-flakes of higher polygons also exist, though they are less common and don't usually have a central polygon. Some examples are shown below; the 8-flake, 10-flake, and 12-flake. While it may not be obvious, these higher polyflakes still contain infinitely many Koch curves, but the angle of the Koch curves decreases as n increases. Their Hausdorff dimensions are slightly more difficult to calculate than lower n-flakes because their scale factor is less obvious. However, the Hausdorff dimension is always less than two but no less than one. An interesting n-flake is the ∞-flake, because as the value of n increases, an n-flake's Hausdorff dimension approaches 1, and when n is infinite, the dimension is 1 and the fractal is a circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
.
In three dimensions
n-flakes can generalized to higher dimensions, in particular to a topological dimension of three. Instead of polygons, regular polyhedra are iteratively replaced. However, while there are an infinite number of regular polygons, there are only five regular, convex polyhedra. Because of this, three-dimensional n-flakes are also called platonic solid fractals. In three dimensions, the fractals' volume is zero.Sierpinski tetrahedron
A Sierpinski tetrahedron is formed by successive flakes of four regular tetrahedrons. Each flake is formed by placing a tetrahedronTetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
scaled by 1/2 in each corner. Its Hausdorff dimension is equal to
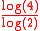, which is exactly equal to 2. On every face there is a Sierpinski triangle and infinitely many are contained within.Hexahedron flake
A hexahedron, or cube, flake defined in the same way as the Sierpinski tetrahedron is simply a cube and is not interesting as a fractal. However, there are two pleasing alternatives. One is the Menger SpongeMenger sponge
In mathematics, the Menger sponge is a fractal curve. It is a universal curve, in that it has topological dimension one, and any other curve is homeomorphic to some subset of it. It is sometimes called the Menger-Sierpinski sponge or the Sierpinski sponge...
, where every cube is replaced by a three dimensional ring of cubes. Its Hausdorff dimension is
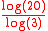≈ 2.7268.Another hexahedron flake can be produced in a manner similar to the Vicsek fractal
Vicsek fractal
In mathematics the Vicsek fractal, also known as Vicsek snowflake or box fractal, is a fractal arising from a construction similar to that of the Sierpinski carpet. It has applications including as compact antennas, particularly in cellular phones....
extended to three dimensions. Every cube is divided into 27 smaller cubes and the center cross is retained, which is the opposite of the Menger sponge
Menger sponge
In mathematics, the Menger sponge is a fractal curve. It is a universal curve, in that it has topological dimension one, and any other curve is homeomorphic to some subset of it. It is sometimes called the Menger-Sierpinski sponge or the Sierpinski sponge...
where the cross is removed. However, it is not the Menger Sponge complement. Its Hausdorff dimension is
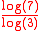≈ 1.7712, because a cross of 7 cubes, each scaled by 1/3, replaces each cube.Octahedron flake
An octahedron flake, or sierpinski octahedron, is formed by successive flakes of six regular octahedrons. Each flake is formed by placing a octahedronOctahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
scaled by 1/2 in each corner. Its Hausdorff dimension is equal to
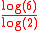≈ 2.5849. On every face there is a Sierpinski triangle and infinitely many are contained within.Dodecahedron flake
A dodecahedron flake, or sierpinski dodecahedron, is formed by successive flakes of twenty regular dodecahedrons. Each flake is formed by placing a dodecahedron scaled by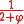 in each corner. Its Hausdorff dimension is equal to 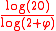≈ 2.3296.Icosahedron flake
An icosahedron flake, or sierpinski icosahedron, is formed by successive flakes of twelve regular icosahedrons. Each flake is formed by placing a icosahedronIcosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
scaled by
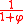in each corner. Its Hausdorff dimension is equal to 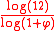≈ 2.5819.