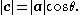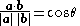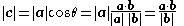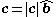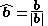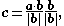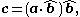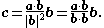Vector resolute
Encyclopedia
The vector projection of a vector  in the direction of a vector
in the direction of a vector 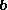 (or "of
(or "of  on/onto
on/onto 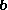 "), is given by:
"), is given by:
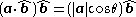
where the operator denotes a dot product
denotes a dot product
,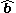 is the unit vector in the direction of
is the unit vector in the direction of 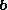 ,
,  is the length of
is the length of  , and
, and 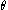 is the angle
is the angle
between and
and 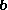 .
.
The other component of (perpendicular to
(perpendicular to 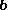 ), called the vector rejection of
), called the vector rejection of  from
from 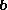 , is given by:
, is given by:
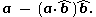
Both the vector projection and the vector rejection are vectors. The vector projection of on
on 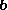 is the orthogonal projection of
is the orthogonal projection of  onto the straight line defined by
onto the straight line defined by 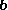 . The corresponding vector rejection is the orthogonal projection of
. The corresponding vector rejection is the orthogonal projection of  onto a plane orthogonal to
onto a plane orthogonal to 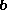 .
.
The vector projection of on
on 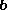 can be also regarded as the corresponding scalar projection
can be also regarded as the corresponding scalar projection 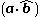 multiplied by
multiplied by 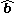 .
.
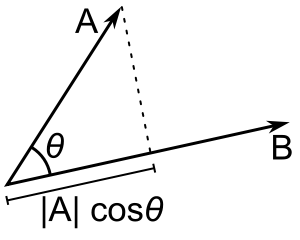 If
If  and
and 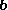 are two vectors, the projection of
are two vectors, the projection of  on
on 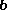 is the vector
is the vector  with the same direction as
with the same direction as 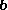 and with the length:
and with the length:
When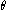 is not known, we can compute
is not known, we can compute 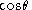 using the following property of the dot product
using the following property of the dot product
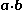 :
:
Thus, the length of can be also computed as follows:
can be also computed as follows:
Since is in the same direction as
is in the same direction as 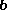 ,
,
where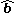 is the unit vector with the same direction as
is the unit vector with the same direction as 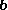 :
:
Substituting, we obtain
which is equivalent to either
or
The latter formula is computationally more efficient than the former. Both require two dot product
s and eventually the multiplication
of a scalar
by a vector, but the former additionally requires a square root
and the division
of a vector by a scalar,
while the latter additionally requires only the division of a scalar by a scalar.
bases
. It is also used in the Separating axis theorem
to detect if two convex shapes intersect.
 in the direction of a vector
in the direction of a vector 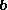 (or "of
(or "of  on/onto
on/onto 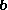 "), is given by:
"), is given by: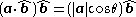
where the operator
 denotes a dot product
denotes a dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
,
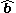 is the unit vector in the direction of
is the unit vector in the direction of 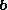 ,
,  is the length of
is the length of  , and
, and 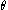 is the angle
is the angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
between
 and
and 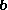 .
.The other component of
 (perpendicular to
(perpendicular to 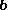 ), called the vector rejection of
), called the vector rejection of  from
from 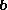 , is given by:
, is given by: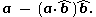
Both the vector projection and the vector rejection are vectors. The vector projection of
 on
on 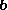 is the orthogonal projection of
is the orthogonal projection of  onto the straight line defined by
onto the straight line defined by 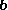 . The corresponding vector rejection is the orthogonal projection of
. The corresponding vector rejection is the orthogonal projection of  onto a plane orthogonal to
onto a plane orthogonal to 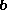 .
.The vector projection of
 on
on 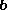 can be also regarded as the corresponding scalar projection
can be also regarded as the corresponding scalar projection 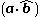 multiplied by
multiplied by 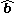 .
.Overview

 and
and 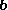 are two vectors, the projection of
are two vectors, the projection of  on
on 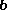 is the vector
is the vector  with the same direction as
with the same direction as 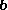 and with the length:
and with the length:
When
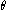 is not known, we can compute
is not known, we can compute 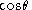 using the following property of the dot product
using the following property of the dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
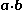 :
:
Thus, the length of
 can be also computed as follows:
can be also computed as follows:
Since
 is in the same direction as
is in the same direction as 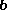 ,
,
where
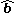 is the unit vector with the same direction as
is the unit vector with the same direction as 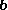 :
:
Substituting, we obtain
which is equivalent to either
or
The latter formula is computationally more efficient than the former. Both require two dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
s and eventually the multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
of a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
by a vector, but the former additionally requires a square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
and the division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
of a vector by a scalar,
while the latter additionally requires only the division of a scalar by a scalar.
Matrix representation
The orthogonal projection can be represented by a projection matrix. To project a vector onto the unit vector a = (ax, ay, az), it would need to be multiplied with this projection matrix: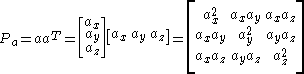
Uses
The vector projection is an important operation in the Gram-Schmidt orthonormalization of vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
bases
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
. It is also used in the Separating axis theorem
Separating axis theorem
For objects lying in a plane , the separating axis theorem states that, given two convex shapes, there exists a line onto which their projections will be separate if and only if they are not intersecting. A line for which the objects have disjoint projections is called a separating axis...
to detect if two convex shapes intersect.
See also
- Scalar projection
- Projection of a vector onto a plane