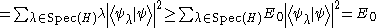Variational method (quantum mechanics)
Encyclopedia
In quantum mechanics
, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state
, and some excited states. The basis for this method is the variational principle
.
The method consists in choosing a "trial wavefunction
" depending on one or more parameter
s, and finding the values of these parameters for which the expectation value
of the energy is the lowest possible. The wavefunction obtained by fixing the parameters to such values is then an approximation to the ground state wavefunction, and the expectation value of the energy in that state is an upper bound
to the ground state energy. The Harris functional
method is anti-variational (it is a lower bound to the energy).
and a Hermitian operator over it called the Hamiltonian
H. Ignoring complications about continuous spectra
, we look at the discrete spectrum
of H and the corresponding eigenspaces of each eigenvalue λ (see spectral theorem for Hermitian operators for the mathematical background):
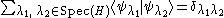
where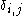
is the Kronecker delta
.
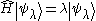Physical states are normalized, meaning that their norm is equal to 1. Once again ignoring complications involved with a continuous spectrum of H, suppose it is bounded from below and that its greatest lower bound is E0. Suppose also that we know the corresponding state |ψ>. The expectation value of H is then
Obviously, if we were to vary over all possible states with norm 1 trying to minimize the expectation value of H, the lowest value would be E0 and the corresponding state would be an eigenstate of E0. Varying over the entire Hilbert space is usually too complicated for physical calculations, and a subspace of the entire Hilbert space is chosen, parametrized by some (real) differentiable parameters αi (i=1,2..,N). The choice of the subspace is called the ansatz
. Some choices of ansatzes lead to better approximations than others, therefore the choice of ansatz is important.
Let's assume there is some overlap between the ansatz and the ground state
(otherwise, it's a bad ansatz). We still wish to normalize the ansatz, so we have the constraints
and we wish to minimize
.
This, in general, is not an easy task, since we are looking for a global minimum and finding the zeroes of the partial derivatives of ε over αi is not sufficient. If ψ (αi) is expressed as a linear combination of other functions (αi being the coefficients), as in the Ritz method
, there is only one minimum and the problem is straightforward. There are other, non-linear methods, however, such as the Hartree-Fock method, that are also not characterized by a multitude of minima and are therefore comfortable in calculations.
There is an additional complication in the calculations described. As ε tends toward E0 in minimization calculations, there is no guarantee that the corresponding trial wavefunctions will tend to the actual wavefunction. This has been demonstrated by calculations using a modified harmonic oscillator as a model system, in which an exactly solvable system is approached using the variational method. A wavefunction different from the exact one is obtained by use of the method described above.
Although usually limited to calculations of the ground state energy, this method can be applied in certain cases to calculations of excited states as well. If the ground state wavefunction is known, either by the method of variation or by direct calculation, a subset of the Hilbert space can be chosen which is orthogonal to the ground state wavefunction.
The resulting minimum is usually not as accurate as for the ground state, as any difference between the true ground state and
results in a lower excited energy. This defect is worsened with each higher excited state.
consists of two electron
s with mass m and electric charge −e surrounding a nucleus
of mass M ≫ m and charge +2e. The Hamiltonian for it, neglecting the kinetic energy of the nucleus and the fine structure
, is:
where ħ is the reduced Planck constant, ε0 is the vacuum permittivity, ri (for i = 1, 2) is the distance of the i-th electron from the nucleus, and |r1 − r2| is the distance between the two electrons.
If the term Vee = e2/(4πε0|r1 − r2|), representing the repulsion between the two electrons, were excluded, the Hamiltonian would become the sum of two hydrogen-like atom
Hamiltonians with nuclear charge +2e. The ground state energy would then be 8E1 = −109 eV, where E1 is the Rydberg constant
, and its ground state wavefunction would be the product of two wavefunctions for the ground state of hydrogen-like atoms:
where a0 is the Bohr radius
. According to the variational principle
, the expectation value of the "full" Hamiltonian H (including the term Vee) in the state described by ψ0 will be a upper bound for its ground state energy. The expectation value of Vee is −5E1/2 = 34 eV, so that of H is 8E1 − 5E1/2 = −75 eV.
A tighter upper bound can be found by using a better trial wavefunction. Each electron can be thought to see the nuclear charge partially "shielded" by the other electron, so we can use a trial wavefunction equal to the product of two wavefunctions for the ground state of hydrogen-like atoms with an "effective" nuclear charge Z < 2:
It can be shown that the expectation value of H in this state is given by ⟨H⟩ = [−2Z2 + (27/4)Z]E1. The value of Z which minimizes this is 27/16 = 1.6875: the other electron somewhat shields the nucleus reducing the effective charge from 2 to about 1.69. Substituting this value of Z into the expression for ⟨H⟩ we find the value 729E1/128 = −77.5 eV,
which is within 2% of the experimental value, −78.975 eV. Even closer estimations of this energy have been found using more complicated trial wave functions with more parameters.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
, and some excited states. The basis for this method is the variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
.
The method consists in choosing a "trial wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
" depending on one or more parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s, and finding the values of these parameters for which the expectation value
Expectation value (quantum mechanics)
In quantum mechanics, the expectation value is the predicted mean value of the result of an experiment. Despite the name, it is not the most probable value of a measurement...
of the energy is the lowest possible. The wavefunction obtained by fixing the parameters to such values is then an approximation to the ground state wavefunction, and the expectation value of the energy in that state is an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
to the ground state energy. The Harris functional
Harris functional
In computational condensed-matter physics, the Harris energy functional is a non-self-consistent approximation to Kohn-Sham density functional theory...
method is anti-variational (it is a lower bound to the energy).
Description
Suppose we are given a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and a Hermitian operator over it called the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
H. Ignoring complications about continuous spectra
Continuous spectrum
The spectrum of a linear operator is commonly divided into three parts: point spectrum, continuous spectrum, and residual spectrum.If H is a topological vector space and A:H \to H is a linear map, the spectrum of A is the set of complex numbers \lambda such that A - \lambda I : H \to H is not...
, we look at the discrete spectrum
Discrete spectrum
In physics, an elementary explanation of a discrete spectrum is that it is an emission spectrum or absorption spectrum for which there is only an integer number of intensities. Atomic electronic absorption and emission spectrum are discrete, as contrasted with, for example, the emission spectrum...
of H and the corresponding eigenspaces of each eigenvalue λ (see spectral theorem for Hermitian operators for the mathematical background):
where
is the Kronecker delta.Physical states are normalized, meaning that their norm is equal to 1. Once again ignoring complications involved with a continuous spectrum of H, suppose it is bounded from below and that its greatest lower bound is E0. Suppose also that we know the corresponding state |ψ>. The expectation value of H is then
Obviously, if we were to vary over all possible states with norm 1 trying to minimize the expectation value of H, the lowest value would be E0 and the corresponding state would be an eigenstate of E0. Varying over the entire Hilbert space is usually too complicated for physical calculations, and a subspace of the entire Hilbert space is chosen, parametrized by some (real) differentiable parameters αi (i=1,2..,N). The choice of the subspace is called the ansatz
Ansatz
Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...
. Some choices of ansatzes lead to better approximations than others, therefore the choice of ansatz is important.
Let's assume there is some overlap between the ansatz and the ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
(otherwise, it's a bad ansatz). We still wish to normalize the ansatz, so we have the constraints
and we wish to minimize
.This, in general, is not an easy task, since we are looking for a global minimum and finding the zeroes of the partial derivatives of ε over αi is not sufficient. If ψ (αi) is expressed as a linear combination of other functions (αi being the coefficients), as in the Ritz method
Ritz method
The Ritz method is a direct method to find an approximate solution for boundary value problems. The method is named after Walter Ritz.In quantum mechanics, a system of particles can be described in terms of an "energy functional" or Hamiltonian, which will measure the energy of any proposed...
, there is only one minimum and the problem is straightforward. There are other, non-linear methods, however, such as the Hartree-Fock method, that are also not characterized by a multitude of minima and are therefore comfortable in calculations.
There is an additional complication in the calculations described. As ε tends toward E0 in minimization calculations, there is no guarantee that the corresponding trial wavefunctions will tend to the actual wavefunction. This has been demonstrated by calculations using a modified harmonic oscillator as a model system, in which an exactly solvable system is approached using the variational method. A wavefunction different from the exact one is obtained by use of the method described above.
Although usually limited to calculations of the ground state energy, this method can be applied in certain cases to calculations of excited states as well. If the ground state wavefunction is known, either by the method of variation or by direct calculation, a subset of the Hilbert space can be chosen which is orthogonal to the ground state wavefunction.
The resulting minimum is usually not as accurate as for the ground state, as any difference between the true ground state and
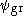results in a lower excited energy. This defect is worsened with each higher excited state.Example: Determining the ground state of the helium atom
The helium atomHelium atom
Helium is an element and the next simplest atom to solve after the hydrogen atom. Helium is composed of two electrons in orbit around a nucleus containing two protons along with either one or two neutrons, depending on the isotope. The hydrogen atom is used extensively to aid in solving the helium...
consists of two electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s with mass m and electric charge −e surrounding a nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
of mass M ≫ m and charge +2e. The Hamiltonian for it, neglecting the kinetic energy of the nucleus and the fine structure
Fine structure
In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to first order relativistic corrections.The gross structure of line spectra is the line spectra predicted by non-relativistic electrons with no spin. For a hydrogenic atom, the gross structure energy...
, is:
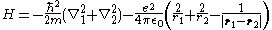
where ħ is the reduced Planck constant, ε0 is the vacuum permittivity, ri (for i = 1, 2) is the distance of the i-th electron from the nucleus, and |r1 − r2| is the distance between the two electrons.
If the term Vee = e2/(4πε0|r1 − r2|), representing the repulsion between the two electrons, were excluded, the Hamiltonian would become the sum of two hydrogen-like atom
Hydrogen-like atom
A hydrogen-like ion is any atomic nucleus with one electron and thus is isoelectronic with hydrogen. Except for the hydrogen atom itself , these ions carry the positive charge e, where Z is the atomic number of the atom. Examples of hydrogen-like ions are He+, Li2+, Be3+ and B4+...
Hamiltonians with nuclear charge +2e. The ground state energy would then be 8E1 = −109 eV, where E1 is the Rydberg constant
Rydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
, and its ground state wavefunction would be the product of two wavefunctions for the ground state of hydrogen-like atoms:
where a0 is the Bohr radius
Bohr radius
The Bohr radius is a physical constant, approximately equal to the most probable distance between the proton and electron in a hydrogen atom in its ground state. It is named after Niels Bohr, due to its role in the Bohr model of an atom...
. According to the variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
, the expectation value of the "full" Hamiltonian H (including the term Vee) in the state described by ψ0 will be a upper bound for its ground state energy. The expectation value of Vee is −5E1/2 = 34 eV, so that of H is 8E1 − 5E1/2 = −75 eV.
A tighter upper bound can be found by using a better trial wavefunction. Each electron can be thought to see the nuclear charge partially "shielded" by the other electron, so we can use a trial wavefunction equal to the product of two wavefunctions for the ground state of hydrogen-like atoms with an "effective" nuclear charge Z < 2:
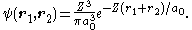
It can be shown that the expectation value of H in this state is given by ⟨H⟩ = [−2Z2 + (27/4)Z]E1. The value of Z which minimizes this is 27/16 = 1.6875: the other electron somewhat shields the nucleus reducing the effective charge from 2 to about 1.69. Substituting this value of Z into the expression for ⟨H⟩ we find the value 729E1/128 = −77.5 eV,
which is within 2% of the experimental value, −78.975 eV. Even closer estimations of this energy have been found using more complicated trial wave functions with more parameters.