Variational message passing
Encyclopedia
Variational message passing (VMP) is an approximate inference
technique for continuous- or discrete-valued Bayesian networks, with conjugate-exponential parents, developed by John Winn. VMP was developed as a means of generalizing the approximate variational methods used by such techniques as Latent Dirichlet allocation
and works by updating an approximate distribution at each node through messages in the node's Markov blanket
.
and observed variables 
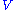, the goal of approximate inference is to lower-bound the probability that a graphical model is in the configuration 
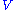. Over some probability distribution 
(to be defined later),
.
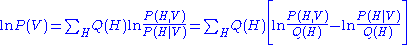So, if we define our lower bound to be
,
then the likelihood is simply this bound plus the relative entropy between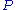
and 
. Because the relative entropy is non-negative, the function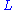 
defined above is indeed a lower bound of the log likelihood of our observation 
. The distribution 
will have a simpler character than that of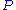 
because marginalizing over 
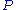is intractable for all but the simplest of graphical models. In particular, VMP uses a factorized distribution 
:
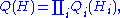
where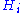
is a disjoint part of the graphical model.
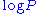improves the approximation of the log likelihood. By substituting in the factorized version of 
, 
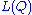, parameterized over the hidden nodes 
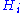as above, is simply the negative relative entropy between 
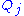and 
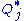plus other terms independent of 
if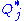 
is defined as
,
where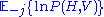
is the expectation over all distributions 
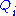except 
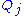. Thus, if we set 
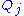to be 
, the bound 
is maximized.
and all parents of nodes are conjugate
to their children nodes, the expectation of the sufficient statistic can be computed from the normalization factor.
) and a gamma distribution (corresponding to the precision, or one over
in more common paramaterizations). Discrete variables can have Dirichlet parents, and Poisson
and exponential
nodes must have gamma parents. However, if the data can be modeled in this manner, VMP offers a generalized framework for providing inference.
Inference
Inference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
technique for continuous- or discrete-valued Bayesian networks, with conjugate-exponential parents, developed by John Winn. VMP was developed as a means of generalizing the approximate variational methods used by such techniques as Latent Dirichlet allocation
Latent Dirichlet allocation
In statistics, latent Dirichlet allocation is a generative model that allows sets of observations to be explained by unobserved groups that explain why some parts of the data are similar...
and works by updating an approximate distribution at each node through messages in the node's Markov blanket
Markov blanket
In machine learning, the Markov blanket for a node A in a Bayesian network is the set of nodes \partial A composed of A's parents, its children, and its children's other parents. In a Markov network, the Markov blanket of a node is its set of neighbouring nodes...
.
Likelihood Lower Bound
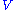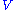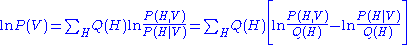Given some set of hidden variables and observed variables , the goal of approximate inference is to lower-bound the probability that a graphical model is in the configuration . Over some probability distribution (to be defined later),.So, if we define our lower bound to be
,then the likelihood is simply this bound plus the relative entropy between
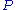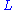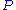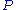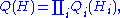
and . Because the relative entropy is non-negative, the function defined above is indeed a lower bound of the log likelihood of our observation . The distribution will have a simpler character than that of because marginalizing over is intractable for all but the simplest of graphical models. In particular, VMP uses a factorized distribution :where
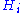is a disjoint part of the graphical model.Determining the Update Rule
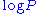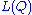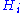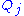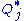The likelihood estimate needs to be as large as possible; because it's a lower bound, getting closer improves the approximation of the log likelihood. By substituting in the factorized version of , , parameterized over the hidden nodes as above, is simply the negative relative entropy between and plus other terms independent of if 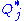is defined as,where
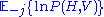is the expectation over all distributions 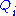except 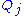. Thus, if we set 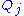to be , the bound is maximized.Messages in Variational Message Passing
Parents send their children the expectation of their sufficient statistic while children send their parents their natural parameter, which also requires messages to be sent from the co-parents of the node.Relationship to Exponential Families
Because all nodes in VMP come from exponential familiesExponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
and all parents of nodes are conjugate
Conjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
to their children nodes, the expectation of the sufficient statistic can be computed from the normalization factor.
VMP Algorithm
The algorithm begins by computing the expected value of the sufficient statistics for that vector. Then, until the likelihood converges to a stable value (this is usually accomplished by setting a small threshold value and running the algorithm until it increases by less than that threshold value), do the following at each node:- Get all messages from parents
- Get all messages from children (this might require the children to get messages from the co-parents)
- Compute the expected value of the nodes sufficient statistics
Constraints
Because every child must be conjugate to its parent, this limits the types of distributions that can be used in the model. For example, the parents of a Gaussian distribution must be a Gaussian distribution (corresponding to the MeanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
) and a gamma distribution (corresponding to the precision, or one over
in more common paramaterizations). Discrete variables can have Dirichlet parents, and PoissonPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
and exponential
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
nodes must have gamma parents. However, if the data can be modeled in this manner, VMP offers a generalized framework for providing inference.
External links
- Infer.NET: an inference framework which includes an implementation of VMP with examples.
- An older implementation of VMP with usage examples.