Variational Monte Carlo
Encyclopedia
In mathematical physics
, variational Monte Carlo (VMC) is a quantum Monte Carlo
method that applies the variational method
to approximate the ground state of the system.
The expectation value necessary can be written in the
representation as
Following the Monte Carlo method
for evaluating integrals, we can interpret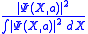
as a probability distribution
function, sample it, and evaluate the energy expectation value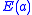
as the average of the local function 
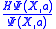, and minimize 
.
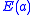VMC is no different from any other variational method, except that since the many-dimensional integrals are evaluated numerically, we only need to calculate the value of the possibly very complicated wave function, which gives a large amount of flexibility to the method. One of the largest gains in accuracy over writing the wave function separably comes from the introduction of the so-called Jastrow factor, where the wave function is written as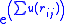
, where 
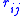is the distance between a pair of quantum particles. With this factor, we can explicitly account for particle-particle correlation, but the many-body integral becomes unseparable, so Monte Carlo is the only way to evaluate it efficiently. In chemical systems, slightly more sophisticated versions of this factor can obtain 80–90% of the correlation energy (see electronic correlation
) with less than 30 parameters. In comparison, a configuration interaction calculation may require around 50,000 parameters to reach that accuracy, although it depends greatly on the particular case being considered. In addition, VMC usually scales as a small power of the number of particles in the simulation, usually something like N2−4 for calculation of the energy expectation value, depending on the form of the wave function.
The problem of function optimization
is a very important research topic in numerical simulation. In QMC, in addition to the usual difficulties to find the minimum of multidimensional parametric function, the statistical noise is present in the estimate of the cost function (usually the energy), and its derivatives, required for an efficient optimization.
Different cost functions and different strategies were used to optimize a many-body trial-function. Usually three cost functions were used in QMC optimization energy, variance or a linear combination of them. The variance optimization method has the advantage that the exact wavefunction's variance is known. (Because the exact wavefunction is an eigenfunction of the Hamiltonian, the variance of the local energy is zero). This means that variance optimization is ideal in that it is bounded by below, it is positive defined and its minimum is known. Energy minimization may ultimately prove more effective, however, as different authors recently showed that the energy optimization is more effective than the variance one.
There are different motivations for this: first, usually one is interested in the lowest energy rather than in the lowest variance in both variational and diffusion Monte Carlo; second, variance optimization takes many iterations to optimize determinant parameters and often the optimization can get stuck in multiple local minimum and it suffers of the "false convergence" problem; third energy-minimized wave functions on average yield more accurate values of other expectation values than variance minimized wave functions do.
The optimization strategies can be divided into three categories. The first strategy is based on correlated sampling together with deterministic optimization methods. Even if this idea yielded very accurate results for the first-row atoms, this procedure can have problems if parameters affect the nodes, and moreover density ratio of the current and initial trial-function increases exponentially with the size of the system. In the second strategy one use a large bin to evaluate the cost function and its derivatives in such way that the noise can be neglected and deterministic methods can be used.
The third approach, is based on an iterative technique to handle directly with noise functions. The first example of these methods is the so called Stochastic Gradient Approximation (SGA), that was used also for structure optimization. Recently an improved and faster approach of this kind was proposed the so called Stochastic Reconfiguration (SR) method.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, variational Monte Carlo (VMC) is a quantum Monte Carlo
Quantum Monte Carlo
Quantum Monte Carlo is a large class of computer algorithms that simulate quantum systems with the idea of solving the quantum many-body problem. They use, in one way or another, the Monte Carlo method to handle the many-dimensional integrals that arise...
method that applies the variational method
Variational method (quantum mechanics)
In quantum mechanics, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state, and some excited states...
to approximate the ground state of the system.
The expectation value necessary can be written in the
representation as
Following the Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
for evaluating integrals, we can interpret
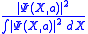
as a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
function, sample it, and evaluate the energy expectation value
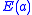as the average of the local function 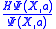, and minimize 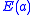.VMC is no different from any other variational method, except that since the many-dimensional integrals are evaluated numerically, we only need to calculate the value of the possibly very complicated wave function, which gives a large amount of flexibility to the method. One of the largest gains in accuracy over writing the wave function separably comes from the introduction of the so-called Jastrow factor, where the wave function is written as
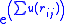, where 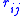is the distance between a pair of quantum particles. With this factor, we can explicitly account for particle-particle correlation, but the many-body integral becomes unseparable, so Monte Carlo is the only way to evaluate it efficiently. In chemical systems, slightly more sophisticated versions of this factor can obtain 80–90% of the correlation energy (see electronic correlationElectronic correlation
Electronic correlation is the interaction between electrons in the electronic structure of a quantum system.- Atomic and molecular systems :...
) with less than 30 parameters. In comparison, a configuration interaction calculation may require around 50,000 parameters to reach that accuracy, although it depends greatly on the particular case being considered. In addition, VMC usually scales as a small power of the number of particles in the simulation, usually something like N2−4 for calculation of the energy expectation value, depending on the form of the wave function.
Wave function optimization in VMC
QMC calculations crucially depend on the quality of the trial-function, and so it is essential to have an optimized wave-function as close as possible to the ground state.The problem of function optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
is a very important research topic in numerical simulation. In QMC, in addition to the usual difficulties to find the minimum of multidimensional parametric function, the statistical noise is present in the estimate of the cost function (usually the energy), and its derivatives, required for an efficient optimization.
Different cost functions and different strategies were used to optimize a many-body trial-function. Usually three cost functions were used in QMC optimization energy, variance or a linear combination of them. The variance optimization method has the advantage that the exact wavefunction's variance is known. (Because the exact wavefunction is an eigenfunction of the Hamiltonian, the variance of the local energy is zero). This means that variance optimization is ideal in that it is bounded by below, it is positive defined and its minimum is known. Energy minimization may ultimately prove more effective, however, as different authors recently showed that the energy optimization is more effective than the variance one.
There are different motivations for this: first, usually one is interested in the lowest energy rather than in the lowest variance in both variational and diffusion Monte Carlo; second, variance optimization takes many iterations to optimize determinant parameters and often the optimization can get stuck in multiple local minimum and it suffers of the "false convergence" problem; third energy-minimized wave functions on average yield more accurate values of other expectation values than variance minimized wave functions do.
The optimization strategies can be divided into three categories. The first strategy is based on correlated sampling together with deterministic optimization methods. Even if this idea yielded very accurate results for the first-row atoms, this procedure can have problems if parameters affect the nodes, and moreover density ratio of the current and initial trial-function increases exponentially with the size of the system. In the second strategy one use a large bin to evaluate the cost function and its derivatives in such way that the noise can be neglected and deterministic methods can be used.
The third approach, is based on an iterative technique to handle directly with noise functions. The first example of these methods is the so called Stochastic Gradient Approximation (SGA), that was used also for structure optimization. Recently an improved and faster approach of this kind was proposed the so called Stochastic Reconfiguration (SR) method.