Electronic correlation
Encyclopedia
Electronic correlation is the interaction between electron
s in the electronic structure of a quantum
system.
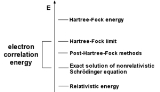
Within the Hartree–Fock method of quantum chemistry
, the antisymmetric wave function is approximated by a single Slater determinant
. Exact wave functions, however, cannot generally be expressed as single determinants. The single-determinant approximation does not take into account Coulomb correlation, leading to a total electronic energy different from the exact solution of the non-relativistic Schrödinger equation
within the Born-Oppenheimer approximation
. Therefore the Hartree–Fock limit is always above this exact energy. The difference is called the correlation energy, a term coined by Löwdin
.
A certain amount of electron correlation is already considered within the HF approximation, found in the electron exchange
term describing the correlation between electrons with parallel spin. This basic correlation prevents two parallel-spin electrons from being found at the same point in space and is often called Fermi correlation. Coulomb correlation, on the other hand, describes the correlation between the spatial position of electrons due to their Coulomb repulsion. There is also a correlation related to the overall symmetry or total spin of the considered system.
The word correlation energy has to be used with caution. First it is usually defined as the energy difference of a correlated method relative to the Hartree-Fock energy. But this is not the full correlation energy because some correlation is already included in HF. Secondly the correlation energy is highly dependent on the basis set
used. The "exact" energy is the energy with full correlation and full basis set.
Electron correlation is sometimes divided into dynamical and non-dynamical (static) correlation. Dynamical correlation is the correlation of the movement of electrons and is described under
electron correlation dynamics and also with the configuration interaction
(CI) method. Static correlation is important for molecules where the ground state is well described only with more than one (nearly-)degenerate determinant. In this case the Hartree-Fock wavefunction (only one determinant) is qualitatively wrong. The multi-configurational self-consistent field
(MCSCF) method takes account of this static correlation but not on the dynamical correlation.
If one wants to calculate excitation energies (energy differences between the ground and excited state
s) one has to be careful that both states are equally balanced (e.g., Multireference configuration interaction
).
To account for electron correlation there are many post-Hartree–Fock methods, including:
One of the most important methods for correcting for the missing correlation is the configuration interaction
(CI) method. It bases on the Hartree-Fock wavefunction and takes a linear combination of excited determinants
as the wavefunction and optimizes the weighting factors 
. When taking all possible excited determinants one speaks of Full-CI. In a Full-CI wavefunction all electrons are fully correlated. For non-small molecules Full-CI is much too computationally expensive. One truncates the CI expansion and gets well-correlated wavefunctions and well-correlated energies. CI is variational
.
Perturbation theory gives correlated energies, but no new wavefunctions. PT is not variational. This means the calculated energy is not an upper bound for the exact energy.
There are also combinations possible. E.g. one can have some nearly degenerate determinants for the multi-configurational self-consistent field
method to account for static correlation and/or some truncated CI method for the biggest part of dynamical correlation and/or on top some pertubational ansatz for small perturbing (unimportant) determinants. Examples for those combinations are CASPT2 and SORCI.
, electrons are typically described with reference to a periodic lattice of atomic nuclei. Non-interacting electrons are therefore typically described by Bloch waves, which correspond to the delocalized, symmetry adapted molecular orbitals used in molecules (while Wannier function
s correspond to localized MOs). A number of important theoretical approximations have been proposed to explain electron correlations in these crystalline systems.
The Fermi liquid
model of correlated electrons in metals is able to explain the temperature dependence of resistivity by electron-electron interactions. It also forms the basis for the BCS theory
of superconductivity
, which is the result of phonon-mediated electron-electron interactions.
Systems that escape a Fermi liquid description are said to be strongly-correlated. In them, interactions plays such an important role that qualitatively new phenomena emerge. This is the case, for example, when the electrons are close to a metal-insulator transition. The Hubbard model
is based on the tight-binding approximation
, and can explain conductor-insulator transitions in Mott insulators such as transition metal oxides
by the presence of repulsive Coulombic interactions between electrons. Its one-dimensional version is considered an archetype of the strong-correlations problem and displays many dramatic manifestations such as quasi-particle fractionalization
. However there is no exact solution of the Hubbard model in more than one dimension.
The RKKY Interaction
can explain electron spin correlations between unpaired inner shell electrons in different atoms in a conducting crystal by a second-order interaction that is mediated by conduction electrons.
The Tomonaga Luttinger Liquid
model approximates second order electron-electron interactions as bosonic interactions.
,
where ρ(ra,rb) represents the joint electronic density, or the probability density of finding electron a at ra and electron b at rb. Within this notation, ρ(ra,rb)dradrb represents the probability of finding the two electrons in their respective volume elements dra and drb.
If these two electrons are correlated, then the probability of finding electron a at a certain position in space depends on the position of electron b, and vice versa. In other words, the product of their independent density functions does not adequately describe the real situation. At small distances, the uncorrelated pair density is too large; at large distances, the uncorrelated pair density is too small (i.e. the electrons tend to "avoid each other").
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s in the electronic structure of a quantum
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
system.
Atomic and molecular systems
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
, the antisymmetric wave function is approximated by a single Slater determinant
Slater determinant
In quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
. Exact wave functions, however, cannot generally be expressed as single determinants. The single-determinant approximation does not take into account Coulomb correlation, leading to a total electronic energy different from the exact solution of the non-relativistic Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
within the Born-Oppenheimer approximation
Born-Oppenheimer approximation
In quantum chemistry, the computation of the energy and wavefunction of an average-size molecule is a formidable task that is alleviated by the Born–Oppenheimer approximation, named after Max Born and J. Robert Oppenheimer. For instance the benzene molecule consists of 12 nuclei and 42...
. Therefore the Hartree–Fock limit is always above this exact energy. The difference is called the correlation energy, a term coined by Löwdin
Per-Olov Löwdin
Per-Olov Löwdin was a Swedish physicist, professor at the University of Uppsala from 1960 to 1983, and in parallel at the University of Florida until 1993....
.
A certain amount of electron correlation is already considered within the HF approximation, found in the electron exchange
Exchange interaction
In physics, the exchange interaction is a quantum mechanical effect without classical analog which increases or decreases the expectation value of the energy or distance between two or more identical particles when their wave functions overlap...
term describing the correlation between electrons with parallel spin. This basic correlation prevents two parallel-spin electrons from being found at the same point in space and is often called Fermi correlation. Coulomb correlation, on the other hand, describes the correlation between the spatial position of electrons due to their Coulomb repulsion. There is also a correlation related to the overall symmetry or total spin of the considered system.
The word correlation energy has to be used with caution. First it is usually defined as the energy difference of a correlated method relative to the Hartree-Fock energy. But this is not the full correlation energy because some correlation is already included in HF. Secondly the correlation energy is highly dependent on the basis set
Basis set (chemistry)
A basis set in chemistry is a set of functions used to create the molecular orbitals, which are expanded as a linear combination of such functions with the weights or coefficients to be determined. Usually these functions are atomic orbitals, in that they are centered on atoms. Otherwise, the...
used. The "exact" energy is the energy with full correlation and full basis set.
Electron correlation is sometimes divided into dynamical and non-dynamical (static) correlation. Dynamical correlation is the correlation of the movement of electrons and is described under
electron correlation dynamics and also with the configuration interaction
Configuration interaction
Configuration interaction is a post-Hartree–Fock linear variational method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multi-electron system. Mathematically, configuration simply describes the linear combination...
(CI) method. Static correlation is important for molecules where the ground state is well described only with more than one (nearly-)degenerate determinant. In this case the Hartree-Fock wavefunction (only one determinant) is qualitatively wrong. The multi-configurational self-consistent field
Multi-configurational self-consistent field
Multi-configurational self-consistent field is a method in quantum chemistry used to generate qualitatively correct reference states of molecules in cases where Hartree–Fock and density functional theory are not adequate...
(MCSCF) method takes account of this static correlation but not on the dynamical correlation.
If one wants to calculate excitation energies (energy differences between the ground and excited state
Excited state
Excitation is an elevation in energy level above an arbitrary baseline energy state. In physics there is a specific technical definition for energy level which is often associated with an atom being excited to an excited state....
s) one has to be careful that both states are equally balanced (e.g., Multireference configuration interaction
Multireference configuration interaction
In quantum chemistry, the multireference configuration interaction method consists in a configuration interaction expansion of the eigenstates of the electronic molecular Hamiltonian in a set of Slater determinants which correspond to excitations of the ground state electronic configuration but...
).
Methods
In simple terms the molecular orbitals of the Hartree-Fock method are optimized by evaluating the energy of an electron in each molecular orbital moving in the mean field of all other electrons, rather than including the instantaneous repulsion between electrons.To account for electron correlation there are many post-Hartree–Fock methods, including:
- configuration interactionConfiguration interactionConfiguration interaction is a post-Hartree–Fock linear variational method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multi-electron system. Mathematically, configuration simply describes the linear combination...
(CI)
One of the most important methods for correcting for the missing correlation is the configuration interaction
Configuration interaction
Configuration interaction is a post-Hartree–Fock linear variational method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multi-electron system. Mathematically, configuration simply describes the linear combination...
(CI) method. It bases on the Hartree-Fock wavefunction and takes a linear combination of excited determinants
as the wavefunction and optimizes the weighting factors . When taking all possible excited determinants one speaks of Full-CI. In a Full-CI wavefunction all electrons are fully correlated. For non-small molecules Full-CI is much too computationally expensive. One truncates the CI expansion and gets well-correlated wavefunctions and well-correlated energies. CI is variationalVariational method (quantum mechanics)
In quantum mechanics, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state, and some excited states...
.
- Møller-Plesset perturbation theoryMøller-Plesset perturbation theoryMøller–Plesset perturbation theory is one of several quantum chemistry post-Hartree–Fock ab initio methods in the field of computational chemistry...
(MP2, MP3, MP4, etc.)
Perturbation theory gives correlated energies, but no new wavefunctions. PT is not variational. This means the calculated energy is not an upper bound for the exact energy.
- multi-configurational self-consistent fieldMulti-configurational self-consistent fieldMulti-configurational self-consistent field is a method in quantum chemistry used to generate qualitatively correct reference states of molecules in cases where Hartree–Fock and density functional theory are not adequate...
(MCSCF)
There are also combinations possible. E.g. one can have some nearly degenerate determinants for the multi-configurational self-consistent field
Multi-configurational self-consistent field
Multi-configurational self-consistent field is a method in quantum chemistry used to generate qualitatively correct reference states of molecules in cases where Hartree–Fock and density functional theory are not adequate...
method to account for static correlation and/or some truncated CI method for the biggest part of dynamical correlation and/or on top some pertubational ansatz for small perturbing (unimportant) determinants. Examples for those combinations are CASPT2 and SORCI.
Crystalline systems
In condensed matter physicsCondensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, electrons are typically described with reference to a periodic lattice of atomic nuclei. Non-interacting electrons are therefore typically described by Bloch waves, which correspond to the delocalized, symmetry adapted molecular orbitals used in molecules (while Wannier function
Wannier function
The Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier.The Wannier functions for different lattice sites in a crystal are orthogonal, allowing a convenient basis for the expansion of electron states in certain regimes...
s correspond to localized MOs). A number of important theoretical approximations have been proposed to explain electron correlations in these crystalline systems.
The Fermi liquid
Fermi liquid
Fermi liquid theory is a theoretical model of interacting fermions that describes the normal state of most metals at sufficiently low temperatures. The interaction between the particles of the many-body system does not need to be small...
model of correlated electrons in metals is able to explain the temperature dependence of resistivity by electron-electron interactions. It also forms the basis for the BCS theory
BCS theory
BCS theory — proposed by Bardeen, Cooper, and Schrieffer in 1957 — is the first microscopic theory of superconductivity since its discovery in 1911. The theory describes superconductivity as a microscopic effect caused by a "condensation" of pairs of electrons into a boson-like state...
of superconductivity
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
, which is the result of phonon-mediated electron-electron interactions.
Systems that escape a Fermi liquid description are said to be strongly-correlated. In them, interactions plays such an important role that qualitatively new phenomena emerge. This is the case, for example, when the electrons are close to a metal-insulator transition. The Hubbard model
Hubbard model
The Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
is based on the tight-binding approximation
Tight binding (physics)
In solid-state physics, the tight binding model is an approach to the calculation of electronic band structure using an approximate set of wave functions based upon superposition of wave functions for isolated atoms located at each atomic site. The method is closely related to the LCAO method used...
, and can explain conductor-insulator transitions in Mott insulators such as transition metal oxides
Transition metal oxides
Transition metal oxides comprise a class of materials that contain transition elements and oxygen. They include insulators as well as metals. Often the same material may display both types of transport properties, hence a Metal-Insulator transition, obtained by varying either temperature or...
by the presence of repulsive Coulombic interactions between electrons. Its one-dimensional version is considered an archetype of the strong-correlations problem and displays many dramatic manifestations such as quasi-particle fractionalization
Fractionalization
In physics, fractionalization is the phenomenon whereby the quasiparticles of a system cannot be constructed as combinations of its elementary constituents...
. However there is no exact solution of the Hubbard model in more than one dimension.
The RKKY Interaction
RKKY
RKKY stands for Ruderman-Kittel-Kasuya-Yosida and refers to a coupling mechanism of nuclear magnetic moments or localized inner d or f shell electron spins in a metal by means of an interaction through the conduction electrons....
can explain electron spin correlations between unpaired inner shell electrons in different atoms in a conducting crystal by a second-order interaction that is mediated by conduction electrons.
The Tomonaga Luttinger Liquid
Luttinger liquid
A Tomonaga-Luttinger liquid, more often referred to as simply a Luttinger liquid, is a theoretical model describing interacting electrons in a one-dimensional conductor...
model approximates second order electron-electron interactions as bosonic interactions.
Mathematical viewpoint
For two independent electrons a and b,,where ρ(ra,rb) represents the joint electronic density, or the probability density of finding electron a at ra and electron b at rb. Within this notation, ρ(ra,rb)dradrb represents the probability of finding the two electrons in their respective volume elements dra and drb.
If these two electrons are correlated, then the probability of finding electron a at a certain position in space depends on the position of electron b, and vice versa. In other words, the product of their independent density functions does not adequately describe the real situation. At small distances, the uncorrelated pair density is too large; at large distances, the uncorrelated pair density is too small (i.e. the electrons tend to "avoid each other").
See also
- Configuration interactionConfiguration interactionConfiguration interaction is a post-Hartree–Fock linear variational method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multi-electron system. Mathematically, configuration simply describes the linear combination...
- Coupled clusterCoupled clusterCoupled cluster is a numerical technique used for describing many-body systems. Its most common use is as one of several quantum chemical post-Hartree–Fock ab initio quantum chemistry methods in the field of computational chemistry...
- Hartree-FockHartree-FockIn computational physics and chemistry, the Hartree–Fock method is an approximate method for the determination of the ground-state wave function and ground-state energy of a quantum many-body system....
- Moller-Plesset
- Post-Hartree-FockPost-Hartree-FockIn computational chemistry, post-Hartree–Fock methods are the set of methods developed to improve on the Hartree–Fock , or self-consistent field method...
- Quantum Monte CarloQuantum Monte CarloQuantum Monte Carlo is a large class of computer algorithms that simulate quantum systems with the idea of solving the quantum many-body problem. They use, in one way or another, the Monte Carlo method to handle the many-dimensional integrals that arise...
- Strongly correlated materialStrongly correlated materialStrongly correlated materials are a wide class of electronic materials that show unusual electronic and magnetic properties, such as metal-insulator transitions or half-metallicity...