
Unrooted binary tree
Encyclopedia
In mathematics and computer science, an unrooted binary tree is an unrooted tree in which each vertex
has either one or three neighbors.
. The vertices with one neighbor are the leaves of the tree, and the remaining vertices are the internal nodes of the tree. The degree
of a vertex is its number of neighbors; in a tree with more than one node, the leaves are the vertices of degree one. An unrooted binary tree is a free tree in which all internal nodes have degree exactly three.
In some applications it may make sense to distinguish subtypes of unrooted binary trees: a planar embedding
of the tree may be fixed by specifying a cyclic ordering for the edges at each vertex, making it into a plane tree. In computer science, binary trees are often rooted and ordered when they are used as data structure
s, but in the applications of unrooted binary trees in hierarchical clustering
and evolutionary tree reconstruction, unordered trees are more common.
Additionally, one may distinguish between trees in which all vertices have distinct labels, trees in which the leaves only are labeled, and trees in which the nodes are not labeled. In an unrooted binary tree with n leaves, there will be n − 1 internal nodes, so the labels may be taken from the set of integers from 1 to 2n − 1 when all nodes are to be labeled, or from the set of integers from 1 to n when only the leaves are to be labeled.
(that is, a rooted tree in which each non-leaf node has exactly two children) by choosing a root edge e of T, placing a new root node in the middle of e, and directing every edge of the resulting subdivided tree away from the root node. Conversely, any full rooted binary tree may be transformed into an unrooted binary tree by removing the root node, replacing the path between its two children by a single undirected edge, and suppressing the orientation of the remaining edges in the graph. For this reason, there are exactly 2n −3 times as many full rooted binary trees with n leaves as there are unrooted binary trees with n leaves.
of a collection of objects may be formalized as a maximal
family of sets
of the objects in which no two sets cross. That is, for every two sets S and T in the family, either S and T are disjoint or one is a subset of the other, and no more sets can be added to the family while preserving this property. If T is an unrooted binary tree, it defines a hierarchical clustering of its leaves: for each edge (u,v) in T there is a cluster consisting of the leaves that are closer to u than to v, and these sets together with the empty set and the set of all leaves form a maximal non-crossing family. Conversely, from any maximal non-crossing family of sets over a set of n elements, one can form a unique unrooted binary tree that has a node for each triple (A,B,C) of disjoint sets in the family that together cover all of the elements.
in which each node describes a species, the leaves represent the species that exist today, and the edges represent ancestor-descendant relationships between species. This tree has a natural orientation from ancestors to descendants, and a root at the common ancestor of the species, so it is a rooted tree. However, some methods of reconstructing binary trees can reconstruct only the nodes and the edges of this tree, but not their orientations.
For instance, cladistic methods
such as maximum parsimony
use as data a set of binary attributes describing features of the species. These methods seek a tree with the given species as leaves in which the internal nodes are also labeled with features, and attempt to minimize the number of times some feature is present at only one of the two endpoints of an edge in the tree. Ideally, each feature should only have one edge for which this is the case. Changing the root of a tree does not change this number of edge differences, so methods based on parsimony are not capable of determining the location of the tree root and will produce an unrooted tree, often an unrooted binary tree.
Unrooted binary trees also are produced by methods for inferring evolutionary trees based on quartet data specifying, for each four leaf species, the unrooted binary tree describing the evolution of those four species, and by methods that use quartet distance
to measure the distance between trees.
s of graphs, by forming an unrooted binary tree whose leaves represent the edges of the given graph. That is, a branch-decomposition may be viewed as a hierarchical clustering of the edges of the graph. Branch-decompositions and an associated numerical quantity, branch-width, are closely related to treewidth and form the basis for efficient dynamic programming
algorithms on graphs.
problem on unrooted binary trees is to count the number of trees with n labeled leaves and unlabeled internal nodes. An unrooted binary tree on n labeled leaves can be formed by connecting the nth leaf to a new node in the middle of any of the edges of an unrooted binary tree on n − 1 labeled leaves. There are 2n − 5 edges at which the nth node can be attached; therefore, the number of trees on n leaves is larger than the number of trees on n − 1 leaves by a factor of 2n − 5. Thus, the number of trees on n labeled leaves is the double factorial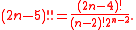
The numbers of trees on 2, 3, 4, 5, ... labeled leaves are
.
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
has either one or three neighbors.
Definitions
A free tree or unrooted tree is a connected undirected graph with no cyclesCycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
. The vertices with one neighbor are the leaves of the tree, and the remaining vertices are the internal nodes of the tree. The degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
of a vertex is its number of neighbors; in a tree with more than one node, the leaves are the vertices of degree one. An unrooted binary tree is a free tree in which all internal nodes have degree exactly three.
In some applications it may make sense to distinguish subtypes of unrooted binary trees: a planar embedding
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
of the tree may be fixed by specifying a cyclic ordering for the edges at each vertex, making it into a plane tree. In computer science, binary trees are often rooted and ordered when they are used as data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
s, but in the applications of unrooted binary trees in hierarchical clustering
Hierarchical clustering
In statistics, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:...
and evolutionary tree reconstruction, unordered trees are more common.
Additionally, one may distinguish between trees in which all vertices have distinct labels, trees in which the leaves only are labeled, and trees in which the nodes are not labeled. In an unrooted binary tree with n leaves, there will be n − 1 internal nodes, so the labels may be taken from the set of integers from 1 to 2n − 1 when all nodes are to be labeled, or from the set of integers from 1 to n when only the leaves are to be labeled.
Rooted binary trees
An unrooted binary tree T may be transformed into a full rooted binary treeBinary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
(that is, a rooted tree in which each non-leaf node has exactly two children) by choosing a root edge e of T, placing a new root node in the middle of e, and directing every edge of the resulting subdivided tree away from the root node. Conversely, any full rooted binary tree may be transformed into an unrooted binary tree by removing the root node, replacing the path between its two children by a single undirected edge, and suppressing the orientation of the remaining edges in the graph. For this reason, there are exactly 2n −3 times as many full rooted binary trees with n leaves as there are unrooted binary trees with n leaves.
Hierarchical clustering
A hierarchical clusteringHierarchical clustering
In statistics, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:...
of a collection of objects may be formalized as a maximal
Maximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
family of sets
Family of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
of the objects in which no two sets cross. That is, for every two sets S and T in the family, either S and T are disjoint or one is a subset of the other, and no more sets can be added to the family while preserving this property. If T is an unrooted binary tree, it defines a hierarchical clustering of its leaves: for each edge (u,v) in T there is a cluster consisting of the leaves that are closer to u than to v, and these sets together with the empty set and the set of all leaves form a maximal non-crossing family. Conversely, from any maximal non-crossing family of sets over a set of n elements, one can form a unique unrooted binary tree that has a node for each triple (A,B,C) of disjoint sets in the family that together cover all of the elements.
Evolutionary trees
According to simple forms of the theory of evolution, the history of life can be summarized as a phylogenetic treePhylogenetic tree
A phylogenetic tree or evolutionary tree is a branching diagram or "tree" showing the inferred evolutionary relationships among various biological species or other entities based upon similarities and differences in their physical and/or genetic characteristics...
in which each node describes a species, the leaves represent the species that exist today, and the edges represent ancestor-descendant relationships between species. This tree has a natural orientation from ancestors to descendants, and a root at the common ancestor of the species, so it is a rooted tree. However, some methods of reconstructing binary trees can reconstruct only the nodes and the edges of this tree, but not their orientations.
For instance, cladistic methods
Cladistics
Cladistics is a method of classifying species of organisms into groups called clades, which consist of an ancestor organism and all its descendants . For example, birds, dinosaurs, crocodiles, and all descendants of their most recent common ancestor form a clade...
such as maximum parsimony
Maximum parsimony
Parsimony is a non-parametric statistical method commonly used in computational phylogenetics for estimating phylogenies. Under parsimony, the preferred phylogenetic tree is the tree that requires the least evolutionary change to explain some observed data....
use as data a set of binary attributes describing features of the species. These methods seek a tree with the given species as leaves in which the internal nodes are also labeled with features, and attempt to minimize the number of times some feature is present at only one of the two endpoints of an edge in the tree. Ideally, each feature should only have one edge for which this is the case. Changing the root of a tree does not change this number of edge differences, so methods based on parsimony are not capable of determining the location of the tree root and will produce an unrooted tree, often an unrooted binary tree.
Unrooted binary trees also are produced by methods for inferring evolutionary trees based on quartet data specifying, for each four leaf species, the unrooted binary tree describing the evolution of those four species, and by methods that use quartet distance
Quartet distance
The quartet distance is a way of measuring the distance between two phylogenetic trees. It is defined as the number of subsets of four leaves that are not related by the same topology in both trees.-Computing the quartet distance:...
to measure the distance between trees.
Branch-decomposition
Unrooted binary trees are also used to define branch-decompositionBranch-decomposition
In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves...
s of graphs, by forming an unrooted binary tree whose leaves represent the edges of the given graph. That is, a branch-decomposition may be viewed as a hierarchical clustering of the edges of the graph. Branch-decompositions and an associated numerical quantity, branch-width, are closely related to treewidth and form the basis for efficient dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
algorithms on graphs.
Enumeration
Because of their applications in hierarchical clustering, the most natural graph enumerationGraph enumeration
In combinatorics, an area of mathematics, graph enumeration describes a class of combinatorial enumeration problems in which one must count undirected or directed graphs of certain types, typically as a function of the number of vertices of the graph...
problem on unrooted binary trees is to count the number of trees with n labeled leaves and unlabeled internal nodes. An unrooted binary tree on n labeled leaves can be formed by connecting the nth leaf to a new node in the middle of any of the edges of an unrooted binary tree on n − 1 labeled leaves. There are 2n − 5 edges at which the nth node can be attached; therefore, the number of trees on n leaves is larger than the number of trees on n − 1 leaves by a factor of 2n − 5. Thus, the number of trees on n labeled leaves is the double factorial
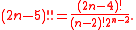
The numbers of trees on 2, 3, 4, 5, ... labeled leaves are
- 1, 1, 3, 15, 105, 945, 10395, 135135, 2027025, 34459425, ... .
Alternative names
Unrooted binary trees have also been called free binary trees, cubic trees, ternary trees and unrooted ternary trees,. However, the "free binary tree" name has also been applied to unrooted trees that may have degree-two nodes and to rooted binary trees with unordered children, and the "ternary tree" name is more frequently used to mean a rooted tree with three children per nodeTernary tree
In computer science, a ternary tree is a tree data structure in which each node has at most three child nodes, usually distinguished as "left", “mid” and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a...
.

