
Universal parabolic constant
Encyclopedia
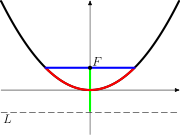
The universal parabolic constant is a mathematical constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
.
It is defined as the ratio, for any parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, of the arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
of the parabolic segment formed by the latus rectum to the focal parameter. It is denoted P2.
In the diagram, the latus rectum is pictured in blue, the parabolic segment that it forms in red and the focal parameter in green.
The value of P2 is
The circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
and parabola are unique among conic sections in that they have a universal constant. The analogous ratios for ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s and hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
s depend on their eccentricities
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
. This means that all circles are similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
and all parabolas are similar, whereas ellipses and hyperbolas are not.
Derivation
Take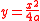 as the equation of the parabola. The focal parameter is
as the equation of the parabola. The focal parameter is  and the semilatus rectum is
and the semilatus rectum is 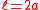 .
.-
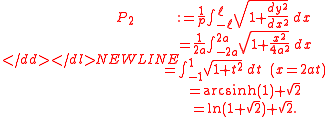
Properties
P2 is a transcendental numberTranscendental numberIn mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
.- Proof. Suppose that P2 is algebraicAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
. Then must also be algebraic. However, by the Lindemann–Weierstrass theoremLindemann–Weierstrass theoremIn mathematics, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states that if 1, ..., are algebraic numbers which are linearly independent over the rational numbers ', then 1, ..., are algebraically...
must also be algebraic. However, by the Lindemann–Weierstrass theoremLindemann–Weierstrass theoremIn mathematics, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states that if 1, ..., are algebraic numbers which are linearly independent over the rational numbers ', then 1, ..., are algebraically...
,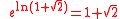 would be transcendental, which is not the case. Hence P2 is transcendental.
would be transcendental, which is not the case. Hence P2 is transcendental.
Since P2 is transcendental, it is also irrationalIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
.
Applications
The average distance from a point randomly selected in the unit square to its center is
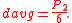
- Proof. Suppose that P2 is algebraic


