Unimodality
Encyclopedia
Unimodality is a term used in several contexts in mathematics
. Originally, it relates to possessing a unique mode
.
In statistics
, a unimodal probability distribution (or when referring to the distribution, a unimodal distribution) is a probability distribution
which has a single mode. As the term "mode" has multiple meanings, so does the term "unimodal".
Strictly speaking, a mode of a discrete probability distribution is a value at which the probability mass function
(pmf) takes its maximum value. In other words, it is a most likely value. A mode of a continuous probability distribution is a value at which the probability density function (pdf) attains its maximum value. Note that in both cases there can be more than one mode, since the maximum value of either the pmf or the pdf can be attained at more than one value.
If there is a single mode, the distribution function is called "unimodal". If it has more modes it is "bimodal" (2), "trimodal" (3), etc., or in general, "multimodal". Figure 1 illustrates normal distributions, which are unimodal. Other examples of unimodal distributions include Cauchy distribution
, Student's t-distribution and chi-squared distribution.
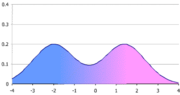
Figure 2 illustrates a bimodal distribution.
Figure 3 illustrates a distribution which by strict definition is unimodal. However, confusingly, and mostly with continuous distributions, when a pdf function has multiple local maxima it is common to refer to all of the local maxima as modes of the distribution. Therefore, if a pdf has more than one local maximum it is referred to as multimodal. Under this common definition, Figure 3 illustrates a bimodal distribution.
In continuous distributions, unimodality can be defined through the behavior of the cumulative distribution function
(cdf). If the cdf is convex
for x < m and concave
for x > m, then the distribution is unimodal, m being the mode. Note that under this definition the uniform distribution
is unimodal, as well as any other distribution in which the maximum distribution is achieved for a range of values, e.g. trapezoidal distribution. Note also that usually this definition allows for a discontinuity at the mode; usually in a continuous distribution the probability of any single value is zero, while this definition allows for a non-zero probability, or an "atom of probability", at the mode.
Criteria for unimodality can also be defined through the characteristic function
of the distribution or through its Laplace–Stieltjes transform.
Another way to define a unimodal discrete distribution is by the occurrence of sign changes in the sequence of differences of the probabilities. A discrete distribution with a probability mass function
,
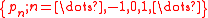, is called unimodal if the sequence 
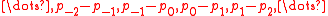has exactly one sign change (when zeroes don't count).
A first important result is Gauss's inequality
. Gauss's inequality gives an upper bound on the probability that a value lies more than any given distance from its mode. This inequality depends on unimodality.
A second is the Vysochanskiï–Petunin inequality, a refinement of the Chebyshev inequality. The Chebyshev inequality guarantees that in any probability distribution, "nearly all" the values are "close to" the mean value. The Vysochanskiï–Petunin inequality refines this to even nearer values, provided that the distribution function is unimodal. Further results were shown by Sellke & Sellke.
s as well.
A common definition is as follows: a function
f(x) is a unimodal function if for some value m , it is monotonically increasing for x ≤ m and monotonically decreasing for x ≥ m. In that case, the maximum value of f(x) is f(m) and there are no other local maxima.
Examples of unimodal functions include Quadratic polynomial
functions with a negative quadratic coefficient, Tent map functions, and more.
The above is sometimes related to as "strong unimodality", from the fact that the monotonicity implied is strong monotonicity. A function f(x) is a weakly unimodal function if for some value m, it is weakly monotonically increasing for x ≤ m and weakly monotonically decreasing for x ≥ m. In that case, the maximum value f(m) can be reached for a continuous range of values of x. An example of a weakly unimodal function which is not strongly unimodal is every other row in a pascal triangle.
Depending on context, unimodal function may also refer to a function that has only one local minimum, rather than maximum. For example, Local unimodal sampling, a method for doing numerical optimization, is often demonstrated with such a function. It can be said that a unimodal function under this extension is a function with a single local extremum.
One important property of unimodal functions is that the extremum can be found using search algorithm
s such as golden section search
, ternary search
or successive parabolic interpolation
.
.
In computational geometry
if a function is unimodal it permits the design of efficient algorithms for finding the extrema of the function.
A more general definition, applicable to a function f(X) of a vector variable X is that f is unimodal if there is a one to one differentiable mapping
X = G(Z) such that f(G(Z)) is convex. Usually one would want G(Z) to be continuously differentiable with nonsingular Jacobian matrix.
Quasiconvex function
s and quasiconcave functions extend the concept of unimodality to functions whose arguments belong to higher-dimensional Euclidean space
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. Originally, it relates to possessing a unique mode
Mode (statistics)
In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
.
Unimodal probability distribution
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a unimodal probability distribution (or when referring to the distribution, a unimodal distribution) is a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
which has a single mode. As the term "mode" has multiple meanings, so does the term "unimodal".
Strictly speaking, a mode of a discrete probability distribution is a value at which the probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
(pmf) takes its maximum value. In other words, it is a most likely value. A mode of a continuous probability distribution is a value at which the probability density function (pdf) attains its maximum value. Note that in both cases there can be more than one mode, since the maximum value of either the pmf or the pdf can be attained at more than one value.
If there is a single mode, the distribution function is called "unimodal". If it has more modes it is "bimodal" (2), "trimodal" (3), etc., or in general, "multimodal". Figure 1 illustrates normal distributions, which are unimodal. Other examples of unimodal distributions include Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
, Student's t-distribution and chi-squared distribution.
Figure 2 illustrates a bimodal distribution.
Figure 3 illustrates a distribution which by strict definition is unimodal. However, confusingly, and mostly with continuous distributions, when a pdf function has multiple local maxima it is common to refer to all of the local maxima as modes of the distribution. Therefore, if a pdf has more than one local maximum it is referred to as multimodal. Under this common definition, Figure 3 illustrates a bimodal distribution.
Other definitions
Other definitions of unimodality in distribution functions also exist.In continuous distributions, unimodality can be defined through the behavior of the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
(cdf). If the cdf is convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
for x < m and concave
Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
for x > m, then the distribution is unimodal, m being the mode. Note that under this definition the uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
is unimodal, as well as any other distribution in which the maximum distribution is achieved for a range of values, e.g. trapezoidal distribution. Note also that usually this definition allows for a discontinuity at the mode; usually in a continuous distribution the probability of any single value is zero, while this definition allows for a non-zero probability, or an "atom of probability", at the mode.
Criteria for unimodality can also be defined through the characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
of the distribution or through its Laplace–Stieltjes transform.
Another way to define a unimodal discrete distribution is by the occurrence of sign changes in the sequence of differences of the probabilities. A discrete distribution with a probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
,
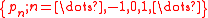, is called unimodal if the sequence 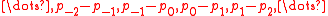has exactly one sign change (when zeroes don't count).Uses and results
One reason for the importance of distribution unimodality is that it allows for several important results. Some examples follow.A first important result is Gauss's inequality
Gauss's inequality
In probability theory, Gauss's inequality gives an upper bound on the probability that a unimodal random variable lies more than any given distance from its mode....
. Gauss's inequality gives an upper bound on the probability that a value lies more than any given distance from its mode. This inequality depends on unimodality.
A second is the Vysochanskiï–Petunin inequality, a refinement of the Chebyshev inequality. The Chebyshev inequality guarantees that in any probability distribution, "nearly all" the values are "close to" the mean value. The Vysochanskiï–Petunin inequality refines this to even nearer values, provided that the distribution function is unimodal. Further results were shown by Sellke & Sellke.
Unimodal function
As the term "modal" applies to data sets and probability distribution, and not in general to functions, the definitions above do not apply. The definition of "unimodal" was extended to functions of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s as well.
A common definition is as follows: a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f(x) is a unimodal function if for some value m , it is monotonically increasing for x ≤ m and monotonically decreasing for x ≥ m. In that case, the maximum value of f(x) is f(m) and there are no other local maxima.
Examples of unimodal functions include Quadratic polynomial
Quadratic polynomial
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
functions with a negative quadratic coefficient, Tent map functions, and more.
The above is sometimes related to as "strong unimodality", from the fact that the monotonicity implied is strong monotonicity. A function f(x) is a weakly unimodal function if for some value m, it is weakly monotonically increasing for x ≤ m and weakly monotonically decreasing for x ≥ m. In that case, the maximum value f(m) can be reached for a continuous range of values of x. An example of a weakly unimodal function which is not strongly unimodal is every other row in a pascal triangle.
Depending on context, unimodal function may also refer to a function that has only one local minimum, rather than maximum. For example, Local unimodal sampling, a method for doing numerical optimization, is often demonstrated with such a function. It can be said that a unimodal function under this extension is a function with a single local extremum.
One important property of unimodal functions is that the extremum can be found using search algorithm
Search algorithm
In computer science, a search algorithm is an algorithm for finding an item with specified properties among a collection of items. The items may be stored individually as records in a database; or may be elements of a search space defined by a mathematical formula or procedure, such as the roots...
s such as golden section search
Golden section search
The golden section search is a technique for finding the extremum of a unimodal function by successively narrowing the range of values inside which the extremum is known to exist. The technique derives its name from the fact that the algorithm maintains the function values for triples of points...
, ternary search
Ternary search
A ternary search algorithm is a technique in computer science for finding the minimum or maximum of a unimodal function...
or successive parabolic interpolation
Successive parabolic interpolation
Successive parabolic interpolation is a technique for finding the extremum of a continuous unimodal function by successively fitting parabolas to the function at three unique points, and at each iteration replacing the "oldest" point with the extremum of the fitted parabola.- Advantages :Only...
.
Other extensions
A function f(x) is "S-unimodal" if its Schwartzian derivative is negative for all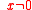.In computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
if a function is unimodal it permits the design of efficient algorithms for finding the extrema of the function.
A more general definition, applicable to a function f(X) of a vector variable X is that f is unimodal if there is a one to one differentiable mapping
X = G(Z) such that f(G(Z)) is convex. Usually one would want G(Z) to be continuously differentiable with nonsingular Jacobian matrix.
Quasiconvex function
Quasiconvex function
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form is a convex set...
s and quasiconcave functions extend the concept of unimodality to functions whose arguments belong to higher-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s.