
Uniform limit theorem
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the uniform limit theorem states that the uniform limit of any sequence of continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s is continuous.
Statement
More precisely, let X be a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, let Y be a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, and let ƒn : X → Y be a sequence of functions converging uniformly to a function ƒ : X → Y. According to the uniform limit theorem, if each of the functions ƒn is continuous, then the limit ƒ must be continuous as well.
This theorem does not hold if uniform convergence is replaced by pointwise convergence
Pointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
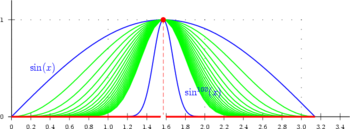
. For example, let ƒn : [0, 1] → R be the sequence of functions ƒn(x) = xn. Then each function ƒn is continuous, but the sequence converges pointwise to the discontinuous function ƒ that is zero on [0, 1) but has ƒ(1) = 1. Another example is shown in the image to the right.
In terms of function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s, the uniform limit theorem says that the space C(X, Y) of all continuous functions from a topological space X to a metric space Y is a closed subset
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
of YX under the uniform metric. In the case where Y is complete, it follows that C(X, Y) is itself a complete metric space. In particular, if Y is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, then C(X, Y) is itself a Banach space under the uniform norm.
The uniform limit theorem also holds if continuity is replaced by uniform continuity
Uniform continuity
In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
. That is, if X and Y are metric spaces and ƒn : X → Y is a sequence of uniformly continuous functions converging uniformly to a function ƒ, then ƒ must be uniformly continuous.
Proof
The uniform limit theorem is proved by the " trick", and is the archetypal example of this trick: to prove a given inequality (
trick", and is the archetypal example of this trick: to prove a given inequality ( ), one uses the axioms to produce 3 inequalities (
), one uses the axioms to produce 3 inequalities (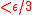 ), and then combines them via the triangle inequality
), and then combines them via the triangle inequalityTriangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
to produce the desired inequality.
History
In 1821, Augustin-Louis Cauchy published a faulty proof that the limit of continuous functions is always continuous. Later Niels Henrik AbelNiels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
found counterexamples. Then Dirichlet analyzed Cauchy's proof and found the error and introduced the missing condition of uniformity.

