
Uniform integrability
Encyclopedia
The concept of uniform integrability is an important concept in functional analysis
and probability theory
.
If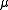 is a finite measure, a subset
is a finite measure, a subset 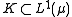 is said to be uniformly integrable if
is said to be uniformly integrable if
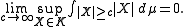
Rephrased with a probabilistic language, the definition becomes : a family of integrable random variables is uniformly integrable if
of integrable random variables is uniformly integrable if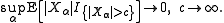
This definition is useful in limit theorems, such as the Vitali convergence theorem
.
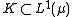 is uniformly integrable iff
is uniformly integrable iff
it is uniformly bounded (i.e.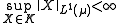 ) and absolutely continuous, i.e. for any
) and absolutely continuous, i.e. for any 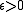 there exists
there exists  so that
so that
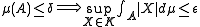 .
.
Dunford
A subset  is uniformly integrable if and only if it is relatively compact for the weak topology
is uniformly integrable if and only if it is relatively compact for the weak topology
.
de la Vallée-Poussin
The family 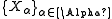 is uniformly integrable iff
is uniformly integrable iff
there exists a nonnegative increasing convex function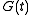 such that
such that 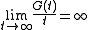 and
and 
Relations to convergence of random variables
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
.
If
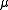 is a finite measure, a subset
is a finite measure, a subset 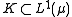 is said to be uniformly integrable if
is said to be uniformly integrable if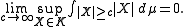
Rephrased with a probabilistic language, the definition becomes : a family
 of integrable random variables is uniformly integrable if
of integrable random variables is uniformly integrable if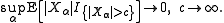
This definition is useful in limit theorems, such as the Vitali convergence theorem
Vitali convergence theorem
In mathematics, the Vitali convergence theorem is a generalization of the better-known dominated convergence theorem of Henri Lebesgue. It is useful when a dominating function cannot be found for the sequence of functions in question; when such a dominating function can be found, Lebesgue's theorem...
.
Sufficient conditions
- If
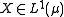 , the singleton
, the singleton 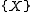 is uniformly integrable, as an easy consequence of Lebesgue's dominated convergence theoremDominated convergence theoremIn measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
is uniformly integrable, as an easy consequence of Lebesgue's dominated convergence theoremDominated convergence theoremIn measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
. Similarly, finite subsets of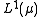 are uniformly integrable.
are uniformly integrable.
- If
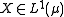 , the set
, the set 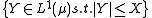 is uniformly integrable.
is uniformly integrable.
- A set bounded in
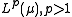 is uniformly integrable.
is uniformly integrable.
Bounded and absolutely continuous
A subset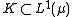 is uniformly integrable iff
is uniformly integrable iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
it is uniformly bounded (i.e.
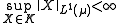 ) and absolutely continuous, i.e. for any
) and absolutely continuous, i.e. for any 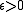 there exists
there exists  so that
so that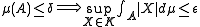 .
. DunfordNelson DunfordNelson Dunford was an American mathematician, known for his work in functional analysis, namely integration of vector valued functions, ergodic theory, and linear operators. The Dunford decomposition, Dunford–Pettis property, and Dunford-Schwartz theorem bear his name.He studied mathematics at the...
–PettisBilly James PettisBilly James Pettis , was an American mathematician, known for his contributions to functional analysis.-See also:*Dunford–Pettis property*Dunford–Pettis theorem*Milman–Pettis theorem*Orlicz–Pettis theorem*Pettis integral...
theorem
A subset  is uniformly integrable if and only if it is relatively compact for the weak topology
is uniformly integrable if and only if it is relatively compact for the weak topologyWeak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
.
de la Vallée-PoussinCharles Jean de la Vallée-PoussinCharles-Jean Étienne Gustave Nicolas de la Vallée Poussin was a Belgian mathematician. He is most well known for proving the Prime number theorem.The king of Belgium ennobled him with the title of baron.-Biography:...
theorem
The family 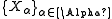 is uniformly integrable iff
is uniformly integrable iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
there exists a nonnegative increasing convex function
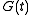 such that
such that 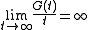 and
and 
Relations to convergence of random variablesConvergence of random variablesIn probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...
- A sequence
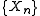 converges to
converges to  in the
in the 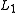 norm if and only if it converges in measureConvergence in measureConvergence in measure can refer to two distinct mathematical concepts which both generalizethe concept of convergence in probability.-Definitions:...
norm if and only if it converges in measureConvergence in measureConvergence in measure can refer to two distinct mathematical concepts which both generalizethe concept of convergence in probability.-Definitions:...
to and it is uniformly integrable.
and it is uniformly integrable.
- In probabilistic language, a sequence of integrable random variables
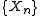 converges to
converges to 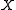 in mean if and only if it converges in probability to
in mean if and only if it converges in probability to 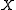 and it is uniformly integrable.
and it is uniformly integrable.

