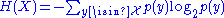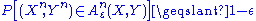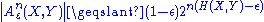Typical set
Encyclopedia
In information theory
, the typical set is a set of sequences whose probability
is close to two raised to the negative power of the entropy
of their source distribution. That this set has total probability
close to one is a consequence of the asymptotic equipartition property
(AEP) which is a kind of law of large numbers
. The notion of typicality is only concerned with the probability of a sequence and not the actual sequence itself.
This has great use in compression
theory as it provides a theoretical means for compressing data, allowing us to represent any sequence Xn using nH(X) bits on average, and, hence, justifying the use of entropy as a measure of information from a source.
The AEP can also be proven for a large class of stationary ergodic process
es, allowing typical set to be defined in more general cases.
, then the typical set, Aε(n)
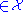(n) is defined as those sequences which satisfy:
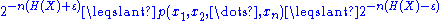
Where
is the information entropy of X. The probability above need only be within a factor of 2nε.
It has the following properties if n is sufficiently large, ε can be chosen arbitrarily small so that:
For a general stochastic process {X(t)} with AEP, the (weakly) typical set can be defined similarly with p(x1, x2, ..., xn) replaced by p(x0τ) (i.e. the probability of the sample limited to the time interval [0, τ]), n being the degree of freedom
of the process in the time interval and H(X) being the entropy rate
. If the process is continuous-valued, differential entropy
is used instead.
, then the strongly typical set, Aε,strong(n)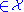
is defined as the set of sequences which satisfy
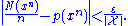
where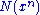
is the number of occurrences of a specific symbol in the sequence.
It can be shown that strongly typical sequences are also weakly typical (with a different constant ε), and hence the name. The two forms, however, are not equivalent. Strong typicality is often easier to work with in proving theorems for memoryless channels. However, as is apparent from the definition, this form of typicality is only defined for random variables having finite support.
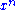and 
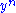are jointly ε-typical if the pair 
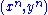is ε-typical with respect to the joint distribution 
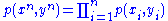and both 
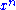and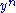 
are ε-typical with respect to their marginal distributions 
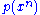and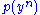 
. The set of all such pairs of sequences 
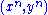is denoted by 
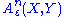. Jointly ε-typical n-tuple sequences are defined similarly.
Let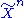
and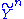 
be two independent sequences of random variables with the same marginal distributions 
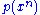and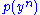 
. Then the set of jointly typical sequences has the following properties:
, typical set encoding encodes only the typical set of a stochastic source with fixed length block codes. Asymptotically, it is, by the AEP, lossless and achieves the minimum rate equal to the entropy rate of the source.
, typical set decoding is used in conjunction with random coding to estimate the transmitted message as the one with a codeword that is jointly ε-typical with the observation. i.e.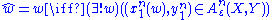
where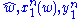
are the message estimate, codeword of message 
and the observation respectively.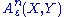 
is defined with respect to the joint distribution 
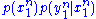where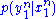 
is the transition probability that characterizes the channel statistics, and 
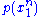is some input distribution used to generate the codewords in the random codebook.
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, the typical set is a set of sequences whose probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
is close to two raised to the negative power of the entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
of their source distribution. That this set has total probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
close to one is a consequence of the asymptotic equipartition property
Asymptotic equipartition property
In information theory the asymptotic equipartition property is a general property of the output samples of a stochastic source. It is fundamental to the concept of typical set used in theories of compression....
(AEP) which is a kind of law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
. The notion of typicality is only concerned with the probability of a sequence and not the actual sequence itself.
This has great use in compression
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
theory as it provides a theoretical means for compressing data, allowing us to represent any sequence Xn using nH(X) bits on average, and, hence, justifying the use of entropy as a measure of information from a source.
The AEP can also be proven for a large class of stationary ergodic process
Stationary ergodic process
In probability theory, stationary ergodic process is a stochastic process which exhibits both stationarity and ergodicity. In essence this implies that the random process will not change its statistical properties with time and that its statistical properties can be deduced from a single,...
es, allowing typical set to be defined in more general cases.
(Weakly) typical sequences (weak typicality, entropy typicality)
If a sequence x1, ..., xn is drawn from an i.i.d. distribution X defined over a finite alphabet, then the typical set, Aε(n)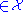(n) is defined as those sequences which satisfy: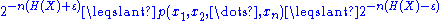Where
is the information entropy of X. The probability above need only be within a factor of 2nε.
It has the following properties if n is sufficiently large, ε can be chosen arbitrarily small so that:
- The probability of a sequence from X being drawn from Aε(n) is greater than 1 − ε
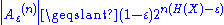
For a general stochastic process {X(t)} with AEP, the (weakly) typical set can be defined similarly with p(x1, x2, ..., xn) replaced by p(x0τ) (i.e. the probability of the sample limited to the time interval [0, τ]), n being the degree of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
of the process in the time interval and H(X) being the entropy rate
Entropy rate
In the mathematical theory of probability, the entropy rate or source information rate of a stochastic process is, informally, the time density of the average information in a stochastic process...
. If the process is continuous-valued, differential entropy
Differential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
is used instead.
Strongly typical sequences (strong typicality, letter typicality)
If a sequence x1, ..., xn is drawn from some specified joint distribution defined over a finite or an infinite alphabet, then the strongly typical set, Aε,strong(n)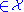 is defined as the set of sequences which satisfy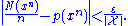where
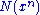is the number of occurrences of a specific symbol in the sequence.It can be shown that strongly typical sequences are also weakly typical (with a different constant ε), and hence the name. The two forms, however, are not equivalent. Strong typicality is often easier to work with in proving theorems for memoryless channels. However, as is apparent from the definition, this form of typicality is only defined for random variables having finite support.
Jointly typical sequences
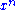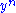Two sequences and are jointly ε-typical if the pair 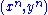is ε-typical with respect to the joint distribution 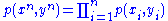and both 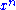and 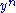are ε-typical with respect to their marginal distributions 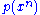and 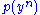. The set of all such pairs of sequences 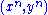is denoted by 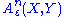. Jointly ε-typical n-tuple sequences are defined similarly.Let
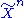and 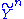be two independent sequences of random variables with the same marginal distributions 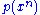and 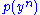. Then the set of jointly typical sequences has the following properties:
Typical set encoding
In communicationCommunication
Communication is the activity of conveying meaningful information. Communication requires a sender, a message, and an intended recipient, although the receiver need not be present or aware of the sender's intent to communicate at the time of communication; thus communication can occur across vast...
, typical set encoding encodes only the typical set of a stochastic source with fixed length block codes. Asymptotically, it is, by the AEP, lossless and achieves the minimum rate equal to the entropy rate of the source.
Typical set decoding
In communicationCommunication
Communication is the activity of conveying meaningful information. Communication requires a sender, a message, and an intended recipient, although the receiver need not be present or aware of the sender's intent to communicate at the time of communication; thus communication can occur across vast...
, typical set decoding is used in conjunction with random coding to estimate the transmitted message as the one with a codeword that is jointly ε-typical with the observation. i.e.
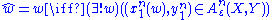
where
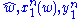are the message estimate, codeword of message and the observation respectively. 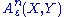is defined with respect to the joint distribution 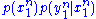where 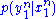is the transition probability that characterizes the channel statistics, and 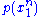is some input distribution used to generate the codewords in the random codebook.Universal channel code
See also
- Asymptotic equipartition propertyAsymptotic equipartition propertyIn information theory the asymptotic equipartition property is a general property of the output samples of a stochastic source. It is fundamental to the concept of typical set used in theories of compression....
- Source coding theorem
- Noisy-channel coding theorem