Asymptotic equipartition property
Encyclopedia
In information theory
the asymptotic equipartition property (AEP) is a general property of the output samples of a stochastic source
. It is fundamental to the concept of typical set
used in theories of compression
.
Roughly speaking, the theorem states that although there are many series of results that may be produced by a random process, the one actually produced is most probably from a loosely-defined set of outcomes that all have approximately the same chance of being the one actually realized. (This is a consequence of the law of large numbers
and ergodic theory
.) Although there are individual outcomes which have a higher probability than any outcome in this set, the vast number of outcomes in the set almost guarantees that the outcome will come from the set.
In the field of Pseudorandom number generation
, a candidate generator of undetermined quality whose output sequence lies too far outside the typical set by some statistical criteria is rejected as insufficiently random. Thus, although the typical set is loosely defined, practical notions arise concerning sufficient typicality.
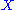on the probability space
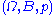, AEP is an assertion that
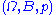
where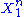
denotes the process limited to duration 
, and 
or simply 
denotes the entropy rate
of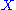
, which must exist for all discrete-time stationary process
es including the ergodic ones. AEP is proved for finite-valued (i.e.
) stationary ergodic stochastic processes in the Shannon-McMillan-Breiman theorem using the ergodic theory and for any i.i.d. sources directly using the law of large numbers in both the discrete-valued case (where 
is simply the entropy
of a symbol) and the continuous-valued case (where
is the differential entropy instead). The definition of AEP can also be extended for certain classes of continuous-time stochastic processes for which a typical set exists for long enough observation time. The convergence is proven almost sure in all cases.
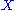is an i.i.d. source, its time series
X1, ..., Xn is i.i.d. with entropy
H(X) in the discrete-valued case and differential entropy
in the continuous-valued case. The weak law of large numbers gives the AEP with convergence in probability,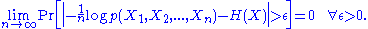
since the entropy is equal to the expectation of
.
The strong law of large number asserts the stronger almost sure convergence,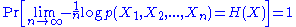
which implies the result from the weak law of large numbers.
, i.e. 
, for the discrete-time stationary ergodic process
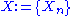defined on the probability space
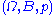. The AEP for such stochastic source, known as the Shannon-McMillan-Breiman theorem, can be shown using the sandwich proof by Algoet and Cover outlined as follows:
We assume that the source is producing independent symbols, with possibly different output statistics at each instant. We assume that the statistics of the process are known completely, that is, the marginal distribution of the process seen at each time instant is known. The joint distribution is just the product of marginals. Then, under the condition (which can be relaxed) that
for all i, for some M>0, the following holds (AEP):
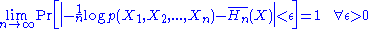
where,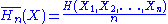
The proof follows from a simple application of Markov's inequality
(applied to second moment of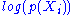
.
It is obvious that the proof holds if any moment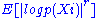
is uniformly bounded for 
(again by Markov's inequality
applied to rth moment).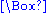
Even this condition is not necessary, but given a non-stationary random process, it should not be difficult to test whether the AEP holds using the above method.
is measurable, we may define the continuous-time stationary process accordingly as 
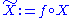. If AEP holds for the discrete-time process, as in the i.i.d. or finite-valued stationary ergodic cases shown above, it automatically holds for the continuous-time stationary process derived from it by some measurable interpolation. i.e.
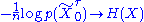
where
corresponds to the degree of freedom in time 
. 
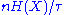and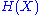 
are the entropy per unit time and per degree of freedom respectively, defined by Shannon.
An important class of such continuous-time stationary process is the bandlimited stationary ergodic process with the sample space being a subset of the continuous
functions. AEP holds if the process is white, in which case the time samples are i.i.d., or there exists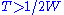 
, where 
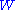is the nominal bandwidth, such that the 
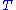-spaced time samples take values in a finite set, in which case we have the discrete-time finite-valued stationary ergodic process.
Any time-invariant operations also preserves AEP, stationarity and ergodicity and we may easily turn a stationary process to non-stationary without losing AEP by nulling out a finite number of time samples in the process.
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
the asymptotic equipartition property (AEP) is a general property of the output samples of a stochastic source
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
. It is fundamental to the concept of typical set
Typical set
In information theory, the typical set is a set of sequences whose probability is close to two raised to the negative power of the entropy of their source distribution. That this set has total probability close to one is a consequence of the asymptotic equipartition property which is a kind of law...
used in theories of compression
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
.
Roughly speaking, the theorem states that although there are many series of results that may be produced by a random process, the one actually produced is most probably from a loosely-defined set of outcomes that all have approximately the same chance of being the one actually realized. (This is a consequence of the law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
and ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
.) Although there are individual outcomes which have a higher probability than any outcome in this set, the vast number of outcomes in the set almost guarantees that the outcome will come from the set.
In the field of Pseudorandom number generation
Pseudorandom number generator
A pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
, a candidate generator of undetermined quality whose output sequence lies too far outside the typical set by some statistical criteria is rejected as insufficiently random. Thus, although the typical set is loosely defined, practical notions arise concerning sufficient typicality.
Definition
Given a discrete-time stationary ergodic stochastic process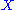 on the probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
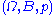, AEP is an assertion that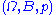where
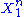denotes the process limited to duration , and or simply denotes the entropy rateEntropy rate
In the mathematical theory of probability, the entropy rate or source information rate of a stochastic process is, informally, the time density of the average information in a stochastic process...
of
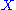, which must exist for all discrete-time stationary processStationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
es including the ergodic ones. AEP is proved for finite-valued (i.e.
) stationary ergodic stochastic processes in the Shannon-McMillan-Breiman theorem using the ergodic theory and for any i.i.d. sources directly using the law of large numbers in both the discrete-valued case (where is simply the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of a symbol) and the continuous-valued case (where
is the differential entropy instead). The definition of AEP can also be extended for certain classes of continuous-time stochastic processes for which a typical set exists for long enough observation time. The convergence is proven almost sure in all cases.AEP for discrete-time i.i.d. sources
Given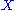 is an i.i.d. source, its time seriesTime series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
X1, ..., Xn is i.i.d. with entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
H(X) in the discrete-valued case and differential entropy
Differential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
in the continuous-valued case. The weak law of large numbers gives the AEP with convergence in probability,
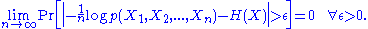
since the entropy is equal to the expectation of
.The strong law of large number asserts the stronger almost sure convergence,
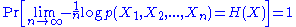
which implies the result from the weak law of large numbers.
AEP for discrete-time finite-valued stationary ergodic sources
Consider a finite-valued sample space, i.e. , for the discrete-time stationary ergodic processStationary ergodic process
In probability theory, stationary ergodic process is a stochastic process which exhibits both stationarity and ergodicity. In essence this implies that the random process will not change its statistical properties with time and that its statistical properties can be deduced from a single,...
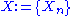defined on the probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
. The AEP for such stochastic source, known as the Shannon-McMillan-Breiman theorem, can be shown using the sandwich proof by Algoet and Cover outlined as follows:
- Let
denote some measurable set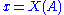 
for some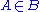 
- Parameterize the joint probability by
and x as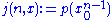 
- Parameterize the conditional probability by
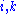and 
as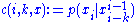 
. - Take the limit of the conditional probability as
and denote it as 
- Argue the two notions of entropy rate
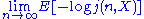and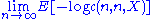 
exist and are equal for any stationary process including the stationary ergodic process 
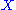. Denote it as 
. - Argue that both
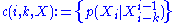and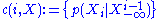 
, where 
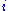is the time index, are stationary ergodic processes, whose sample means converge almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
to some values denoted by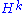
and 
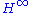respectively. - Define the
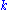-th order Markov approximation to the probability 
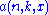as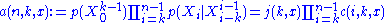
- Argue that
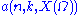is finite from the finite-value assumption. - Express
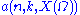in terms of the sample mean of 
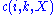and show that it converges almost surely to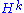 
- Define
, which is a probability measure. - Express
in terms of the sample mean of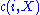 
and show that it converges almost surely to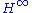 
- Argue that
as 
using the stationarity of the process. - Argue that
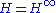using the Lévy's martingale convergence theorem and the finite-value assumption. - Show that
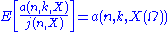which is finite as argued before. - Show that
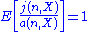by conditioning on the infinite past 
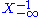and iterating the expectation. - Show that
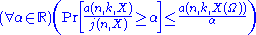using the Markov's inequalityMarkov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
and the expectation derived previously. - Similarly, show that
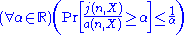, which is equivalent to 
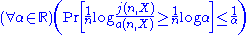. - Show that
of both 
and 
are non-positive almost surely by setting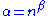 
for any 
and applying the Borel-Cantelli lemmaBorel-Cantelli lemmaIn probability theory, the Borel–Cantelli lemma is a theorem about sequences of events. In general, it is a result in measure theory. It is named after Émile Borel and Francesco Paolo Cantelli...
. - Show that
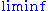and 
of 
are lower and upper bounded almost surely by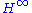 
and 
respectively by breaking up the logarithms in the previous result. - Complete the proof by pointing out that the upper and lower bounds are shown previously to approach
as 
.
AEP for non-stationary discrete-time source producing independent symbols
The assumptions of stationarity/ergodicity/identical distribution of random variables is not essential for the AEP to hold. Indeed, as is quite clear intuitively, the AEP requires only some form of the law of large numbers to hold, which is fairly general. However, the expression needs to be suitably generalized, and the conditions need to be formulated precisely.We assume that the source is producing independent symbols, with possibly different output statistics at each instant. We assume that the statistics of the process are known completely, that is, the marginal distribution of the process seen at each time instant is known. The joint distribution is just the product of marginals. Then, under the condition (which can be relaxed) that
for all i, for some M>0, the following holds (AEP):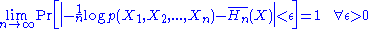where,
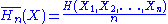
- Proof
The proof follows from a simple application of Markov's inequality
Markov's inequality
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
(applied to second moment of
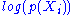.It is obvious that the proof holds if any moment
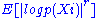is uniformly bounded for (again by Markov's inequalityMarkov's inequality
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
applied to rth moment).
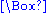
Even this condition is not necessary, but given a non-stationary random process, it should not be difficult to test whether the AEP holds using the above method.
Applications for AEP for non-stationary source producing independent symbols
The AEP for non-stationary discrete-time independent process leads us to (among other results) source coding theorem for non-stationary source (with independent output symbols) and channel coding theorem for non-stationary memoryless channels.Source Coding Theorem
The source coding theorem for discrete time non-stationary independent sources can be found here: source coding theoremChannel Coding Theorem
Channel coding theorem for discrete time non-stationary memoryless channels can be found here: noisy channel coding theoremNoisy channel coding theorem
In information theory, the noisy-channel coding theorem , establishes that for any given degree of noise contamination of a communication channel, it is possible to communicate discrete data nearly error-free up to a computable maximum rate through the channel...
AEP for certain continuous-time stationary ergodic sources
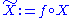Discrete-time functions can be interpolated to continuous-time functions. If such interpolation is measurable, we may define the continuous-time stationary process accordingly as . If AEP holds for the discrete-time process, as in the i.i.d. or finite-valued stationary ergodic cases shown above, it automatically holds for the continuous-time stationary process derived from it by some measurable interpolation. i.e.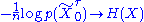where
corresponds to the degree of freedom in time . 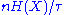and 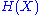are the entropy per unit time and per degree of freedom respectively, defined by Shannon.An important class of such continuous-time stationary process is the bandlimited stationary ergodic process with the sample space being a subset of the continuous
functions. AEP holds if the process is white, in which case the time samples are i.i.d., or there exists 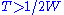, where 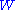is the nominal bandwidth, such that the 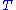-spaced time samples take values in a finite set, in which case we have the discrete-time finite-valued stationary ergodic process.Any time-invariant operations also preserves AEP, stationarity and ergodicity and we may easily turn a stationary process to non-stationary without losing AEP by nulling out a finite number of time samples in the process.
The Classic Paper
- Claude E. Shannon. A Mathematical Theory of CommunicationA Mathematical Theory of Communication"A Mathematical Theory of Communication" is an influential 1948 article by mathematician Claude E. Shannon. As of November 2011, Google Scholar has listed more than 48,000 unique citations of the article and the later-published book version...
. Bell System Technical Journal, July/October 1948.
Other Journal Articles
- Paul H. Algoet and Thomas M. Cover. A Sandwich Proof of the Shannon-McMillan-Breiman Theorem. The Annals of Probability, 16(2): 899-909, 1988.
- Sergio Verdu and Te Sun Han. The Role of the Asymptotic Equipartition Property in Noiseless Source Coding. IEEE Transactions on Information Theory, 43(3): 847-857, 1997.
Textbooks on Information Theory
- Thomas M. Cover, Joy A. Thomas. Elements of Information Theory New York: Wiley, 1991. ISBN 0-471-06259-6
- David J. C. MacKay. Information Theory, Inference, and Learning Algorithms Cambridge: Cambridge University Press, 2003. ISBN 0-521-64298-1