Turingery
Encyclopedia
Turingery or Turing's Method (playfully dubbed Turingismus by Peter Ericsson, Peter Hilton
and Donald Michie
) was a hand codebreaking method devised by the mathematician and cryptanalyst Alan Turing
at the British Government Code and Cypher School at Bletchley Park
during World War II
. It was for use against in Cryptanalysis of the Lorenz cipher
produced by the SZ40 and SZ42
teleprinter rotor scrambler machines
, one of the Germans
' Geheimschreiber (secret writer) machines. The British codenamed non-Morse
traffic Fish
, and that from this machine Tunny.
Reading a Tunny message required firstly that the logical structure of the system was known, secondly that the periodically-changed pattern of active cams on the wheels was derived, and thirdly that the starting positions of the scrambler wheels for this message—the message key
—was established. The logical structure of Tunny had been worked out by William Tutte
and colleagues over several months ending in January 1942. Deriving the message key was called setting at Bletchley Park, but it was the derivation of the cam patterns—which was known as wheel breaking—that was the target of Turingery.
German operator errors in transmitting more than one message with the same key, producing a depth, allowed the derivation of that key. Turingery was applied to such a key to derive the cam settings.
The SZ machines were 12-wheel rotor
cipher
machines which implemented a Vernam stream cipher
. They were attached in-line to standard Lorenz teleprinters. The message characters were encoded in the 5-bit
International Telegraphy Alphabet No. 2 (ITA2). The output ciphertext characters were generated by combining a pseudorandom
character-by-character key stream with the input characters using the exclusive or (XOR) function (symbolised by ⊕ ).
Similarly, for deciphering, the ciphertext was combined with the key to give the plaintext.
This produces the essential reciprocity to allow the same machine with the same settings to be used for both enciphering and deciphering.
Each of the five bits of the key for each character was generated by the relevant wheels in two parts of the machine. These were termed the chi
(
) wheels, and the psi
(
) wheels. The chi wheels all moved on one position for each character. The psi wheels also all moved together, but not after each character. Their movement was controlled by the two mu
(
) or motor wheels.
The key stream generated by the SZ machines thus had a chi component and a psi component that were combined together with the XOR function. So, the key that was combined with the plaintext for enciphering—or with the ciphertext for deciphering—can be represented as follows.
Symbolically:
The twelve wheels each had a series of cams (or pins) around them. These cams could be set in a raised or lowered position. In the raised position they generated a mark ' x ' (1 in binary), in the lowered position they generated a space ' • ' (0 in binary). The number of cams on each wheel equalled the number of impulses needed to cause them to complete a full rotation. It should be noted that these numbers are all co-prime
with each other, giving the longest possible time before the pattern repeated. With a total of 501 cams this equals 2501 which is approximately 10151, an astronomically large number. However, if the five impulses are considered independently, the numbers are much more manageable. The product
of the rotation period of any pair of chi wheels gives numbers between 41×31=1271 and 26×23=598.
2 subtraction (without borrow)—and, incidentally, modulo 2 addition (without carry). So, for the characters in the key(K), the difference ΔK was obtained as follows:
Similarly with the plaintext, the ciphertext and the two components of the key. Also, the relationship amongst them applies when they are differenced. For example, as well as:
It is the case that:
If the plaintext is represented by P and the cipertext by Z, the following also hold true:
Peter Hilton
Peter John Hilton was a British mathematician, noted for his contributions to homotopy theory and for code-breaking during the Second World War.-Life:Hilton was born in London, and educated at St Paul's School...
and Donald Michie
Donald Michie
Donald Michie was a British researcher in artificial intelligence. During World War II, Michie worked for the Government Code and Cypher School at Bletchley Park, contributing to the effort to solve "Tunny," a German teleprinter cipher.-Early life and career:Michie was born in Rangoon, Burma...
) was a hand codebreaking method devised by the mathematician and cryptanalyst Alan Turing
Alan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
at the British Government Code and Cypher School at Bletchley Park
Bletchley Park
Bletchley Park is an estate located in the town of Bletchley, in Buckinghamshire, England, which currently houses the National Museum of Computing...
during World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
. It was for use against in Cryptanalysis of the Lorenz cipher
Cryptanalysis of the Lorenz cipher
Cryptanalysis of the Lorenz cipher was the process that enabled the British to read secret German military messages during World War II. The British Government Code and Cypher School at Bletchley Park decrypted many communications between the German High Command in Berlin and their army commands...
produced by the SZ40 and SZ42
Lorenz cipher
The Lorenz SZ40, SZ42A and SZ42B were German rotor cipher machines used by the German Army during World War II. They were developed by C. Lorenz AG in Berlin. They implemented a Vernam stream cipher...
teleprinter rotor scrambler machines
Rotor machine
In cryptography, a rotor machine is an electro-mechanical device used for encrypting and decrypting secret messages. Rotor machines were the cryptographic state-of-the-art for a prominent period of history; they were in widespread use in the 1920s–1970s...
, one of the Germans
Germans
The Germans are a Germanic ethnic group native to Central Europe. The English term Germans has referred to the German-speaking population of the Holy Roman Empire since the Late Middle Ages....
' Geheimschreiber (secret writer) machines. The British codenamed non-Morse
Morse
Morse can refer to:* Morse code, a method of coding messages into long and short beeps-Places:Canada* Morse , Saskatchewan* Morse, Saskatchewan, a hamlet* Morse No...
traffic Fish
Fish (cryptography)
Fish was the Allied codename for any of several German teleprinter stream ciphers used during World War II. Enciphered teleprinter traffic was used between German High Command and Army Group commanders in the field, so its intelligence value was of the highest strategic value to the Allies...
, and that from this machine Tunny.
Reading a Tunny message required firstly that the logical structure of the system was known, secondly that the periodically-changed pattern of active cams on the wheels was derived, and thirdly that the starting positions of the scrambler wheels for this message—the message key
Key (cryptography)
In cryptography, a key is a piece of information that determines the functional output of a cryptographic algorithm or cipher. Without a key, the algorithm would produce no useful result. In encryption, a key specifies the particular transformation of plaintext into ciphertext, or vice versa...
—was established. The logical structure of Tunny had been worked out by William Tutte
W. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
and colleagues over several months ending in January 1942. Deriving the message key was called setting at Bletchley Park, but it was the derivation of the cam patterns—which was known as wheel breaking—that was the target of Turingery.
German operator errors in transmitting more than one message with the same key, producing a depth, allowed the derivation of that key. Turingery was applied to such a key to derive the cam settings.
The SZ40 and SZ42
The logical functioning of the Tunny system was worked out well before the Bletchley Park cryptanalysts saw one of the machines—which only happened in 1945, shortly before the allied victory in Europe.Rotor machine
In cryptography, a rotor machine is an electro-mechanical device used for encrypting and decrypting secret messages. Rotor machines were the cryptographic state-of-the-art for a prominent period of history; they were in widespread use in the 1920s–1970s...
cipher
Cipher
In cryptography, a cipher is an algorithm for performing encryption or decryption — a series of well-defined steps that can be followed as a procedure. An alternative, less common term is encipherment. In non-technical usage, a “cipher” is the same thing as a “code”; however, the concepts...
machines which implemented a Vernam stream cipher
Stream cipher
In cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...
. They were attached in-line to standard Lorenz teleprinters. The message characters were encoded in the 5-bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
International Telegraphy Alphabet No. 2 (ITA2). The output ciphertext characters were generated by combining a pseudorandom
Pseudorandom number generator
A pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
character-by-character key stream with the input characters using the exclusive or (XOR) function (symbolised by ⊕ ).
Similarly, for deciphering, the ciphertext was combined with the key to give the plaintext.
This produces the essential reciprocity to allow the same machine with the same settings to be used for both enciphering and deciphering.
Each of the five bits of the key for each character was generated by the relevant wheels in two parts of the machine. These were termed the chi
Chi (letter)
Chi is the 22nd letter of the Greek alphabet, pronounced as in English.-Greek:-Ancient Greek:Its value in Ancient Greek was an aspirated velar stop .-Koine Greek:...
(
) wheels, and the psiPsi (letter)
Psi is the 23rd letter of the Greek alphabet and has a numeric value of 700. In both Classical and Modern Greek, the letter indicates the combination /ps/ . The letter was adopted into the Old Italic alphabet, and its shape is continued into the Algiz rune of the Elder Futhark...
(
) wheels. The chi wheels all moved on one position for each character. The psi wheels also all moved together, but not after each character. Their movement was controlled by the two muMu (letter)
Carlos Alberto Vives Restrepo is a Grammy Award and three-time Latin Grammy Award winning-Colombian singer, composer and actor.-Biography:...
(
) or motor wheels.The key stream generated by the SZ machines thus had a chi component and a psi component that were combined together with the XOR function. So, the key that was combined with the plaintext for enciphering—or with the ciphertext for deciphering—can be represented as follows.
Symbolically:
The twelve wheels each had a series of cams (or pins) around them. These cams could be set in a raised or lowered position. In the raised position they generated a mark ' x ' (1 in binary), in the lowered position they generated a space ' • ' (0 in binary). The number of cams on each wheel equalled the number of impulses needed to cause them to complete a full rotation. It should be noted that these numbers are all co-prime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
with each other, giving the longest possible time before the pattern repeated. With a total of 501 cams this equals 2501 which is approximately 10151, an astronomically large number. However, if the five impulses are considered independently, the numbers are much more manageable. The product
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
of the rotation period of any pair of chi wheels gives numbers between 41×31=1271 and 26×23=598.
Differencing
Cryptanalysis often involves finding patterns of some sort that provide a way into eliminating a range of key possibilities. At Bletchley Park the XOR combination of the values of two adjacent letters in the key or the ciphertext was called the difference (symbolised by the Greek letter delta 'Δ') because XOR is the same as moduloModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
2 subtraction (without borrow)—and, incidentally, modulo 2 addition (without carry). So, for the characters in the key(K), the difference ΔK was obtained as follows:
Similarly with the plaintext, the ciphertext and the two components of the key. Also, the relationship amongst them applies when they are differenced. For example, as well as:
It is the case that:
If the plaintext is represented by P and the cipertext by Z, the following also hold true:
And:
The reason that differencing provided a way into Tunny, was that although the frequency distribution of characters in the ciphertext could not be distinguished from a random stream, the same was not true for a version of the ciphertext from which the chi element of the key had been removed. This is because, where the plaintext contained a repeated character and the psi wheels did not move on, the differenced psi character (Δ
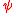) would be the null character (••••• or 00000), or, in Bletchley Park terminology, '/'. When XOR-ed with any character, this null character has no effect, so in these circumstances, Δ
= ΔK. Repeated characters in the plaintext were more frequent both because of the characteristics of German (LL, SS, MM and FF are relatively common), and because telegraphists frequently repeated the figures-shift and letters-shift characters as their loss in an ordinary telegraph message could lead to gibberish.To quote the General Report on Tunny:
Turingery introduced the principle that the key differenced at one, now called ΔΚ, could yield information unobtainable from ordinary key. This Δ principle was to be the fundamental basis of nearly all statistical methods of wheel-breaking and setting.
Bit-level differencing
As well as applying diferencing to the full 5-bit characters of the ITA2 code, it was also applied to the individual impulses (bits). So, for the first impulse, that was enciphered by wheels
1 and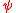 
1, differenced at one:And for the second impulse:
And so on.
It is also worth noting that the periodicity of the chi and psi wheels (41 and 43 respectively for the first impulse) is reflected in the pattern of ΔKj. However, given that the psi wheels did not advance for every input character, as did the chi wheels, it was not simply a repetition of the pattern every 41 × 43 = 1763 characters for ΔK1, but a more complex sequence.
Turing's method
On his return to Bletchley Park from America in April 1943, Turing was less involved in the day-to-day work of Hut 8, and spent a few weeks in the Research Section. He had become interested in the problem of breaking Tunny from the keys that had been obtained from depths. In July, he developed the method of deriving the cam settings from a length of key. It involved an iterativeIteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
, almost trial-and-error, process. It relied on the fact that when the differenced psi character is the null character (••••• or 00000), /, then XOR-ing this with any other character does not change it. Thus the delta key character gives the character of the five chi wheels (i.e. Δ
= ΔK).Given that the delta psi character was the null character half of the time on average, an assumption that ΔK = Δ
had a 50% chance of being correct. The process started by treating a particular ΔK character as being the Δ
for that position. The resulting putative bit pattern of x and • for each chi wheel, was recorded on a sheet of paper that contained as many columns as there were characters in the key, and five rows representing the five impulses of the Δ
. Given the knowledge from Tutte's work, of the periodicity of each of the wheels, this allowed the propagation of these values at the appropriate positions in the rest of the key.A set of five sheets, one for each of the chi wheels, was also prepared. These contained a set of columns corresponding in number to the cams for the appropriate chi wheel, and were referred to as a 'cage'. So the
3 cage had 29 such columns. Successive 'guesses' of Δ
values then produced further putative cam state values. These might either agree or disagree with previous assumptions, and a count of agreements and disagreements was made on these sheets. Where disagreements substantially outweighed agreements, the assumption was made that the Δ
character was not the null character /, so the relevant assumption was discounted. Progressively, all the cam settings of the chi wheels were deduced, and from them the psi and motor wheel cam settings.As experience of the method developed, improvements were made that allowed it to be used with much shorter lengths of key than the original 500 or so characters.