Truth table reduction
Encyclopedia
In computability theory
, a truth-table reduction is a reduction
from one set of natural numbers to another.
As a "tool", it is weaker than Turing reduction, since not every Turing reduction between sets can be performed by a truth-table reduction, but every truth-table reduction can be performed by a Turing reduction. For the same reason it is said to be a stronger reducibility than Turing reducibility, because it implies Turing reducibility. A weak truth-table reduction is a related type of reduction which is so named because it weakens the constraints placed on a truth-table reduction, and provides a weaker equivalence classification; as such, a "weak truth-table reduction" can actually be more powerful than a truth-table reduction as a "tool", and perform a reduction which is not performable by truth table.
A Turing reduction
from a set B to a set A computes the membership of a single element in A by asking questions about the membership of various elements in B during the computation; it may adaptively determine which questions it asks based upon answers to previous questions. In contrast, a truth-table reduction or a weak truth-table reduction must present all of its (finitely many) oracle queries at the same time. In a truth-table reduction, the reduction also gives a boolean function (a truth table) which, when given the answers to the queries, will produce the final answer of the reduction. In a weak truth-table reduction, the reduction uses the oracle answers as a basis for further computation which may depend on the given answers but may not ask further questions of the oracle.
Equivalently, a weak truth-table reduction is a Turing reduction for which the use of the reduction is bounded by a computable function. For this reason, they are sometimes referred to as bounded Turing (bT) reductions rather than as weak truth-table (wtt) reductions.
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, a truth-table reduction is a reduction
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
from one set of natural numbers to another.
As a "tool", it is weaker than Turing reduction, since not every Turing reduction between sets can be performed by a truth-table reduction, but every truth-table reduction can be performed by a Turing reduction. For the same reason it is said to be a stronger reducibility than Turing reducibility, because it implies Turing reducibility. A weak truth-table reduction is a related type of reduction which is so named because it weakens the constraints placed on a truth-table reduction, and provides a weaker equivalence classification; as such, a "weak truth-table reduction" can actually be more powerful than a truth-table reduction as a "tool", and perform a reduction which is not performable by truth table.
A Turing reduction
Turing reduction
In computability theory, a Turing reduction from a problem A to a problem B, named after Alan Turing, is a reduction which solves A, assuming B is already known . It can be understood as an algorithm that could be used to solve A if it had available to it a subroutine for solving B...
from a set B to a set A computes the membership of a single element in A by asking questions about the membership of various elements in B during the computation; it may adaptively determine which questions it asks based upon answers to previous questions. In contrast, a truth-table reduction or a weak truth-table reduction must present all of its (finitely many) oracle queries at the same time. In a truth-table reduction, the reduction also gives a boolean function (a truth table) which, when given the answers to the queries, will produce the final answer of the reduction. In a weak truth-table reduction, the reduction uses the oracle answers as a basis for further computation which may depend on the given answers but may not ask further questions of the oracle.
Equivalently, a weak truth-table reduction is a Turing reduction for which the use of the reduction is bounded by a computable function. For this reason, they are sometimes referred to as bounded Turing (bT) reductions rather than as weak truth-table (wtt) reductions.
Properties
As every truth-table reduction is a Turing reduction, if A is truth-table reducible to B (A ≤tt B), then A is also Turing reducible to B (A ≤T B). Considering also one-one reducibility, many-one reducibility and weak truth-table reducibility, one gets the following chain of implications:-
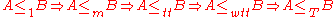; one-one reducibility implies many-one reducibility, which implies truth-table reducibility, which in turn implies weak truth-table reducibility, which in turn implies Turing reducibility.