
Tube domain
Encyclopedia
In mathematics
, a tube domain is a generalization of the notion of a vertical strip (or half-plane) in the complex plane
to several complex variables
. A strip can be thought of as the collection of complex numbers whose real part lie in a given subset of the real line and whose imaginary part is unconstrained; likewise, a tube is the set of complex vectors whose real part is in some given collection of real vectors, and whose imaginary part is unconstrained.
Tube domains are domains of the Laplace transform of a function of several real
variables (see multidimensional Laplace transform). Hardy space
s on tubes can be defined in a manner in which a version of the Paley–Wiener theorem from one variable continues to hold, and characterizes the elements of Hardy spaces as the Laplace transforms of functions with appropriate integrability properties. Tubes over convex set
s are domains of holomorphy
. The Hardy spaces on tubes over convex cones have an especially rich structure, so that precise results are known concerning the boundary values of Hp functions. In mathematical physics, the future tube is the tube domain associated to the interior of the past null cone in Minkowski space
, and has applications in relativity theory and quantum gravity
. Certain tubes over cones support a Bergman metric
in terms of which they become bounded symmetric domains. One of these is the Siegel half-space which is fundamental in arithmetic
.
coordinate space. Then any element of Cn can be decomposed into real and imaginary parts: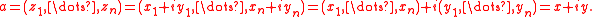
Let A be an open
subset of Rn. The tube over A, denoted TA, is the subset of Cn consisting of all elements whose real parts lie in A:
of the tube , which is also a tube, and in fact

Since any convex open set is a domain of holomorphy
, a convex tube is also a domain of holomorphy. So the holomorphic envelope of any tube is equal to its convex hull.
in Rn. The Hardy space
H p(TA) is the set of all holomorphic function
s F in TA such that
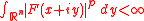
for all x in A.
In the special case of p = 2, functions in H2(TA) can be characterized as follows. Let ƒ be a complex-valued function on Rn satisfying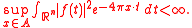
The Fourier–Laplace transform of ƒ is defined by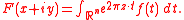
Then F is well-defined and belongs to H2(TA). Conversely, every element of H2(TA) has this form.
A corollary of this characterization is that H2(TA) contains a nonzero function if and only if A contains no straight line.
convex set
such that, whenever x lies in A, so does the entire ray from the origin to x. Symbolically,
If A is a cone, then the elements of H2(TA) have L2 boundary limits in the sense that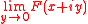
exists in L2(B). There is an analogous result for Hp(TA), but it requires additional regularity of the cone (specifically, the dual cone A* needs to have nonempty interior).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a tube domain is a generalization of the notion of a vertical strip (or half-plane) in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
to several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. A strip can be thought of as the collection of complex numbers whose real part lie in a given subset of the real line and whose imaginary part is unconstrained; likewise, a tube is the set of complex vectors whose real part is in some given collection of real vectors, and whose imaginary part is unconstrained.
Tube domains are domains of the Laplace transform of a function of several real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
variables (see multidimensional Laplace transform). Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
s on tubes can be defined in a manner in which a version of the Paley–Wiener theorem from one variable continues to hold, and characterizes the elements of Hardy spaces as the Laplace transforms of functions with appropriate integrability properties. Tubes over convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
s are domains of holomorphy
Domain of holomorphy
In mathematics, in the theory of functions of several complex variables, a domain of holomorphy is a set which is maximal in the sense that there exists a holomorphic function on this set which cannot be extended to a bigger set....
. The Hardy spaces on tubes over convex cones have an especially rich structure, so that precise results are known concerning the boundary values of Hp functions. In mathematical physics, the future tube is the tube domain associated to the interior of the past null cone in Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, and has applications in relativity theory and quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
. Certain tubes over cones support a Bergman metric
Bergman metric
In differential geometry, the Bergman metric is a Hermitian metric that can be defined on certain types of complex manifold. It is so called because it is derived from the Bergman kernel, both of which are named for Stefan Bergman.-Definition:...
in terms of which they become bounded symmetric domains. One of these is the Siegel half-space which is fundamental in arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
.
Definition
Let Rn denote real coordinate space of dimension n and Cn denote complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
coordinate space. Then any element of Cn can be decomposed into real and imaginary parts:
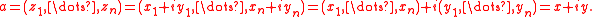
Let A be an open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
subset of Rn. The tube over A, denoted TA, is the subset of Cn consisting of all elements whose real parts lie in A:

Tubes as domains of holomorphy
Suppose that A is a connected open set. Then any complex-valued function that is holomorphic in a tube TA can be extended uniquely to a holomorphic function on the convex hullConvex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the tube , which is also a tube, and in fact

Since any convex open set is a domain of holomorphy
Domain of holomorphy
In mathematics, in the theory of functions of several complex variables, a domain of holomorphy is a set which is maximal in the sense that there exists a holomorphic function on this set which cannot be extended to a bigger set....
, a convex tube is also a domain of holomorphy. So the holomorphic envelope of any tube is equal to its convex hull.
Hardy spaces
Let A be an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in Rn. The Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
H p(TA) is the set of all holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s F in TA such that
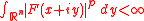
for all x in A.
In the special case of p = 2, functions in H2(TA) can be characterized as follows. Let ƒ be a complex-valued function on Rn satisfying
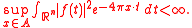
The Fourier–Laplace transform of ƒ is defined by
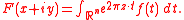
Then F is well-defined and belongs to H2(TA). Conversely, every element of H2(TA) has this form.
A corollary of this characterization is that H2(TA) contains a nonzero function if and only if A contains no straight line.
Tubes over cones
Let A be an open convex cone in Rn. This means that A is an openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
such that, whenever x lies in A, so does the entire ray from the origin to x. Symbolically,

If A is a cone, then the elements of H2(TA) have L2 boundary limits in the sense that
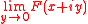
exists in L2(B). There is an analogous result for Hp(TA), but it requires additional regularity of the cone (specifically, the dual cone A* needs to have nonempty interior).

