Transitive reduction
Encyclopedia
In mathematics
, a transitive reduction of a binary relation
R on a set X is a minimal relation
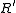on X such that the transitive closure
of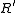
is the same as the transitive closure of R. If the transitive closure of R is antisymmetric
and finite, then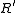
is unique. However, neither existence nor uniqueness of transitive reductions is guaranteed in general.
, any binary relation
R on a set X may be thought of as a directed graph
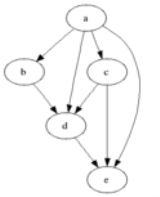
(V, A), where V = X is the vertex set and A = R is the set of arcs of the graph. The transitive reduction of a graph is sometimes referred to as its minimal representation. The following image displays drawings of graphs corresponding to a non-transitive binary relation (on the left) and its transitive reduction (on the right).
The transitive reduction of a finite directed acyclic graph
is unique.
The transitive reduction of a finite partially ordered set
is its covering relation
, which is given visual expression by means of a Hasse diagram
.
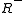of an acyclic relation 
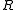can be computed using its transitive closure 
:
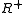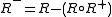
Here,
denotes relation composition.
, which introduced the term in this meaning, also proves a connection between transitive closure
and reduction:
The tred tool in the Graphviz
toolset transitively reduces a graph, using a depth-first search
-based implementation.
described in their well-cited Maintenance Of Transitive Closures And Transitive Reductions Of Graphs an algorithm for simultaneously keeping track of both the transitive closure and transitive reduction of a graph in this incremental fashion.
The algorithm uses
time for a sequence of consecutive edge insertions and
time for a sequence of consecutive edge deletions, where Eold is the edge set prior to the insertions or deletions and Enew is the edge set afterwards. For acyclic graphs, the deletion algorithm requires only
time. These times are still best-known, as more recent research has preferred to focus on transitive closure.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a transitive reduction of a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
R on a set X is a minimal relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
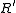on X such that the transitive closureTransitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of
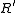is the same as the transitive closure of R. If the transitive closure of R is antisymmetricAntisymmetric relation
In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
and finite, then
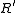is unique. However, neither existence nor uniqueness of transitive reductions is guaranteed in general.Example
In graph theoryGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, any binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
R on a set X may be thought of as a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
(V, A), where V = X is the vertex set and A = R is the set of arcs of the graph. The transitive reduction of a graph is sometimes referred to as its minimal representation. The following image displays drawings of graphs corresponding to a non-transitive binary relation (on the left) and its transitive reduction (on the right).
The transitive reduction of a finite directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
is unique.
The transitive reduction of a finite partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
is its covering relation
Covering relation
In mathematics, especially order theory, the covering relation of a partially ordered set is the binary relation which holds between comparable elements that are immediate neighbours...
, which is given visual expression by means of a Hasse diagram
Hasse diagram
In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
.
Graph algorithms for transitive reduction
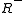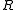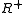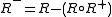
The transitive reduction of an acyclic relation can be computed using its transitive closure :Here,
denotes relation composition., which introduced the term in this meaning, also proves a connection between transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
and reduction:
- they extend the computation of transitive reduction from transitive closure to deal with cycles;
- they give a construction to compute a graph's transitive closure from its transitive reduction;
- thus, transitive closure and transitive reduction have the same time complexityTime complexityIn computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
.
The tred tool in the Graphviz
Graphviz
Graphviz is a package of open-source tools initiated by AT&T Labs Research for drawing graphs specified in DOT language scripts. It also provides libraries for software applications to use the tools...
toolset transitively reduces a graph, using a depth-first search
Depth-first search
Depth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....
-based implementation.
Incremental data structures
One of the most well-studied problems in computational graph theory is that of incrementally keeping track of the transitive closure of a graph while performing a sequence of insertions and deletions of vertices and edges. In 1987, J.A. La Poutré and Jan van LeeuwenJan van Leeuwen
Jan van Leeuwen is a Dutch computer scientist, a professor at the Department of Information and Computing Sciences at the Utrecht University....
described in their well-cited Maintenance Of Transitive Closures And Transitive Reductions Of Graphs an algorithm for simultaneously keeping track of both the transitive closure and transitive reduction of a graph in this incremental fashion.
The algorithm uses
- O(|Enew||V|)
time for a sequence of consecutive edge insertions and
- O(|Eold||V|+|Eold|2)
time for a sequence of consecutive edge deletions, where Eold is the edge set prior to the insertions or deletions and Enew is the edge set afterwards. For acyclic graphs, the deletion algorithm requires only
- O(|Eold||V|)
time. These times are still best-known, as more recent research has preferred to focus on transitive closure.