
Tarski's high school algebra problem
Encyclopedia
In mathematical logic
, Tarski's high school algebra problem was a question posed by Alfred Tarski
. It asks whether there are identities
involving addition
, multiplication
, and exponentiation
over the positive integers that cannot be proved using eleven axioms about these operations that are taught in high school-level mathematics. The question was solved in 1980 by Alex Wilkie
who showed that such unprovable identities do exist.
These eleven axioms, sometimes called the high school identities, are related to the axioms of an exponential ring
. Tarski's problem then becomes: are there identities involving only addition, multiplication, and exponentiation, that are true for all positive integers, but that cannot be proved using only the axioms 1–11?
Here brackets are omitted when axiom 2. tells us that there is no confusion about grouping.
The length of proofs is not an issue; proofs of similar identities to that above for things like (x + y)100 would take a lot of lines, but would really involve little more than the above proof.
, although they were obviously known and used by mathematicians long before then. Dedekind was the first, though, who seemed to be asking if these axioms were somehow sufficient to tell us everything we could want to know about the integers. The question was put on a firm footing as a problem in logic and model theory
sometime in the 1960s by Alfred Tarski, and by the 1980s it had become known as Tarski's high school algebra problem.

This identity is usually denoted W(x,y) and is true for all positive integers x and y, as can be seen by factoring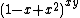 out of the second terms; yet it cannot be proved true using the eleven high school axioms.
out of the second terms; yet it cannot be proved true using the eleven high school axioms.
Intuitively, the identity cannot be proved because the high school axioms can't be used to discuss the polynomial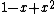 . Reasoning about that polynomial and the subterm
. Reasoning about that polynomial and the subterm 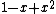 requires a concept of negation or subtraction, and these are not present in the high school axioms. Lacking this, it is then impossible to use the axioms to manipulate the polynomial and prove true properties about it. Wilkie's results from his paper show, in more formal language, that the "only gap" in the high school axioms is the inability to manipulate polynomials with negative coefficients.
requires a concept of negation or subtraction, and these are not present in the high school axioms. Lacking this, it is then impossible to use the axioms to manipulate the polynomial and prove true properties about it. Wilkie's results from his paper show, in more formal language, that the "only gap" in the high school axioms is the inability to manipulate polynomials with negative coefficients.
it has also been proved that if one restricts the kinds of exponential one takes then the above eleven axioms are sufficient to prove every true statement.
Another problem stemming from Wilkie's result that remains open is that which asks what the smallest algebra
is for which W(x, y) is not true but the eleven axioms above are. In 1985 an algebra with 59 elements was found that satisfied the axioms but for which W(x, y) was false. Smaller such algebras have since been found, and it is now known that the smallest such one must have between 11 and 12 elements.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, Tarski's high school algebra problem was a question posed by Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
. It asks whether there are identities
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
involving addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, and exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
over the positive integers that cannot be proved using eleven axioms about these operations that are taught in high school-level mathematics. The question was solved in 1980 by Alex Wilkie
Alex Wilkie
Alex Wilkie FRS is a British mathematician known for his contributions to Model theory and logic. Previously Reader in Mathematical Logic at the University of Oxford, he was appointed to the Fielden Chair of Pure Mathematics at the University of Manchester in 2007.Wilkie attended Aylesbury...
who showed that such unprovable identities do exist.
Statement of the problem
Tarski considered the following eleven axioms about addition ('+'), multiplication ('·'), and exponentiation to be standard axioms taught in high school:- x + y = y + x
- (x + y) + z = x + (y + z)
- x · 1 = x
- x · y = y · x
- (x · y) · z = x · (y · z)
- x · (y + z) = x · y + x ·z
- 1x = 1
- x1 = x
- xy + z = xy · xz
- (x · y)z = xz · yz
- (xy)z = xy · z.
These eleven axioms, sometimes called the high school identities, are related to the axioms of an exponential ring
Exponential field
In mathematics, an exponential field is a field that has an extra operation on its elements which extends the usual idea of exponentiation.-Definition:...
. Tarski's problem then becomes: are there identities involving only addition, multiplication, and exponentiation, that are true for all positive integers, but that cannot be proved using only the axioms 1–11?
Example of a provable identity
Since the axioms seem to list all the basic facts about the operations in question it is not immediately obvious that there should be anything one can state using only the three operations that is not provably true. However, proving seemingly innocuous statements can require long proofs using only the above eleven axioms. Consider the following proof that (x + 1)2 = x2 + 2 · x + 1:2- = (x + 1)1 + 1
- = (x + 1)1 · (x + 1)1 by 9.
- = (x + 1) · (x + 1) by 8.
- = (x + 1) · x + (x + 1) · 1 by 6.
- = x · (x + 1) + x + 1 by 4. and 3.
- = x · x + x · 1 + x · 1 + 1 by 6. and 3.
- = x1 · x1 + x · (1 + 1) + 1 by 8. and 6.
- = x1 + 1 + x · 2 + 1 by 9.
- = x2 + 2 · x + 1 by 4.
Here brackets are omitted when axiom 2. tells us that there is no confusion about grouping.
The length of proofs is not an issue; proofs of similar identities to that above for things like (x + y)100 would take a lot of lines, but would really involve little more than the above proof.
History of the problem
The list of eleven axioms can be found explicitly written down in the works of Richard DedekindRichard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, although they were obviously known and used by mathematicians long before then. Dedekind was the first, though, who seemed to be asking if these axioms were somehow sufficient to tell us everything we could want to know about the integers. The question was put on a firm footing as a problem in logic and model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
sometime in the 1960s by Alfred Tarski, and by the 1980s it had become known as Tarski's high school algebra problem.
Solution
In 1980 Alex Wilkie proved that not every identity in question can be proved using the axioms above. He did this by explicitly finding such an identity. By introducing new function symbols corresponding to polynomials that map positive numbers to positive numbers he proved this identity, and showed that these functions together with the eleven axioms above were both sufficient and necessary to prove it. The identity in question is
This identity is usually denoted W(x,y) and is true for all positive integers x and y, as can be seen by factoring
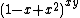 out of the second terms; yet it cannot be proved true using the eleven high school axioms.
out of the second terms; yet it cannot be proved true using the eleven high school axioms.Intuitively, the identity cannot be proved because the high school axioms can't be used to discuss the polynomial
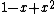 . Reasoning about that polynomial and the subterm
. Reasoning about that polynomial and the subterm 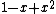 requires a concept of negation or subtraction, and these are not present in the high school axioms. Lacking this, it is then impossible to use the axioms to manipulate the polynomial and prove true properties about it. Wilkie's results from his paper show, in more formal language, that the "only gap" in the high school axioms is the inability to manipulate polynomials with negative coefficients.
requires a concept of negation or subtraction, and these are not present in the high school axioms. Lacking this, it is then impossible to use the axioms to manipulate the polynomial and prove true properties about it. Wilkie's results from his paper show, in more formal language, that the "only gap" in the high school axioms is the inability to manipulate polynomials with negative coefficients.Generalisations
Wilkie proved that there are statements about the positive integers that cannot be proved using the eleven axioms above and showed what extra information is needed before such statements can be proved. Using Nevanlinna theoryNevanlinna theory
Nevanlinna theory is a branch of complex analysis developed by Rolf Nevanlinna. It deals with the value distribution theory of holomorphic functions in one variable, usually denoted z....
it has also been proved that if one restricts the kinds of exponential one takes then the above eleven axioms are sufficient to prove every true statement.
Another problem stemming from Wilkie's result that remains open is that which asks what the smallest algebra
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
is for which W(x, y) is not true but the eleven axioms above are. In 1985 an algebra with 59 elements was found that satisfied the axioms but for which W(x, y) was false. Smaller such algebras have since been found, and it is now known that the smallest such one must have between 11 and 12 elements.

