Tanaka's formula
Encyclopedia
In the stochastic calculus
, Tanaka's formula states that
where Bt is the standard Brownian motion
, sgn denotes the sign function
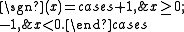
and Lt is its local time
at 0 (the local time spent by B at 0 before time t) given by the L2-limit
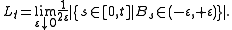
Tanaka's formula is the explicit Doob–Meyer decomposition of the submartingale |Bt| into the martingale
part (the integral
on the right-hand side), and a continuous increasing process (local time). It can also be seen as the analogue of Ito's Lemma
for the (nonsmooth) absolute value function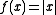
, with 
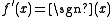and 
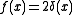; see local time
for a formal explanation of the Ito term.
|x| is not C2
in x at x = 0, so we cannot apply Ito's formula directly. But if we approximate it near zero (i.e. in [−ε, ε]) by parabola
s
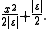
And using Ito's formula we can then take the limit
as ε → 0, leading to Tanaka's formula.
Stochastic calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes...
, Tanaka's formula states that
where Bt is the standard Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, sgn denotes the sign function
Sign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
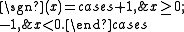
and Lt is its local time
Local time (mathematics)
In the mathematical theory of stochastic processes, local time is a stochastic process associated with diffusion processes such as Brownian motion, that characterizes the amount of time a particle has spent at a given level...
at 0 (the local time spent by B at 0 before time t) given by the L2-limit
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
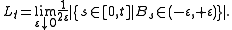
Tanaka's formula is the explicit Doob–Meyer decomposition of the submartingale |Bt| into the martingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
part (the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
on the right-hand side), and a continuous increasing process (local time). It can also be seen as the analogue of Ito's Lemma
Ito's lemma
In mathematics, Itō's lemma is used in Itō stochastic calculus to find the differential of a function of a particular type of stochastic process. It is named after its discoverer, Kiyoshi Itō...
for the (nonsmooth) absolute value function
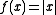, with 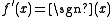and 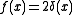; see local timeLocal time (mathematics)
In the mathematical theory of stochastic processes, local time is a stochastic process associated with diffusion processes such as Brownian motion, that characterizes the amount of time a particle has spent at a given level...
for a formal explanation of the Ito term.
Outline of proof
The functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
|x| is not C2
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
in x at x = 0, so we cannot apply Ito's formula directly. But if we approximate it near zero (i.e. in [−ε, ε]) by parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
s
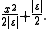
And using Ito's formula we can then take the limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
as ε → 0, leading to Tanaka's formula.