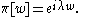
System of imprimitivity
Encyclopedia
The concept of system of imprimitivity is used in mathematics
, particularly in algebra
and analysis
, both within the context of the theory
of group representation
s. It was used by George Mackey
as the basis for his theory of induced unitary representation
s of locally compact group
s.
The simplest case, and the context in which the idea was first noticed, is that of finite group
s (see primitive permutation group
). Consider a group G and subgroups H and K, with K contained in H. Then the left coset
s of H in G are each the union of left cosets of K. Not only that, but translation (on one side) by any element g of G respects this decomposition. The connection with induced representation
s is that the permutation representation on cosets is the special case of induced representation, in which a representation is induced from a trivial representation
. The structure, combinatorial in this case, respected by translation shows that either K is a maximal subgroup
of G, or there is a system of imprimitivity (roughly, a lack of full 'mixing'). In order to generalise this to other cases, the concept is re-expressed: first in terms of functions on G constant on K-cosets, and then in terms of projection operators (for example the averaging over K-cosets of elements of the group algebra
).
Mackey also used the idea for his explication of quantization theory based on preservation of relativity groups acting on configuration space
. This generalized work of Eugene Wigner and others and is often considered to be one of the pioneering ideas in canonical quantization
.
s.
Suppose G is a finite group and U is a representation of G on a finite-dimensional complex vector space H. The action of G on elements of H induces an action
of G on the vector subspaces of H in an obvious way:
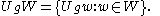
Suppose X is a set of subspaces of H such that (1) X is permuted by the action of G on subspaces and (2) H is the (internal) algebraic direct sum of the spaces in X, written

Then (U, X) is a system of imprimitivity for G.
Two assertions must hold in the above definition:
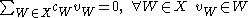
only holds when all the coefficients cW are zero.
If the action of G on the elements of X is transitive, then we say this is a transitive system of imprimitivity.
Suppose G is a finite group, G0 a subgroup of G. A representation U of G is induced from a representation V of G0 if and only if there exist the following:
such that G0 is the fixed point subgroup of W under the action of G, i.e.
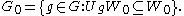
and V is equivalent to the representation of G0
on W0 given by Uh | W0 for h ∈ G0. Note that by this definition, induced by is a relation between representations. We would like to show that there is actually a mapping on representations which corresponds to this relation.
For finite groups one can easily show that a well-defined
inducing construction exists on equivalence of representations by considering the character
of a representation U defined by
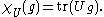
In fact if a representation U of G is induced from a representation V of G0, then
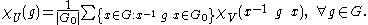
Thus the character function χU (and therefore U itself) is completely determined by χV.
of G on H is defined by
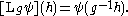
Now H can be considered as the algebraic direct sum of the one dimensional spaces Wx, for x ∈ G, where
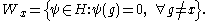
The spaces Wx are permuted by Lg.
s.
Mackey's original formulation was expressed in terms of a locally compact second countable (lcsc) group G, a standard Borel space X and a Borel group action
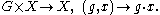
We will refer to this as a standard Borel G-space.
The definitions can be given in a much more general context, but the original setup used by Mackey is still quite general and requires fewer technicalities.
Definition. Let G be a lcsc group acting on a standard Borel space X. A system of imprimitivity based on (G, X) consists of a separable Hilbert space
H and a pair consisting of
which satisfy
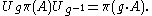
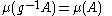
for all g ∈ G and Borel subsets A of G.
Let π(A) be multiplication by the indicator function of A and Ug be the operator
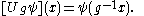
Then (U, π) is a system of imprimitivity of (G, X) on L2μ(X).
This system of imprimitivity is sometimes called the Koopman system of imprimitivity.
the corresponding projection-valued measure π on X is homogeneous of multiplicity n. In fact, X breaks up into a countable disjoint family {Xn} 1 ≤ n ≤ ω of Borel sets such that π is homogeneous of multiplicity n on Xn. It is also easy to show Xn is G invariant.
Lemma. Any system of imprimitivity is an orthogonal direct sum of homogeneous ones.
It can be shown that if the action of G on X is transitive, then any system of imprimitivity on X is homogeneous. More generally, if the action of G on X is ergodic (meaning that X cannot be reduced by invariant proper Borel sets of X) then any system of imprimitivity on X is homogeneous.
We now discuss how the structure of homogeneous systems of imprimitivity can be expressed in a form which generalizes the Koopman representation given in the example above.
In the following, we assume that μ is a σ-finite measure on a standard Borel G-space X such that the action of G respects the measure class of μ. This condition is weaker than invariance, but it suffices to construct a unitary translation operator similar to the Koopman operator in the example above. G respects the measure class of μ means that the Radon-Nikodym derivative
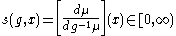
is well-defined for every g ∈ G, where
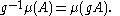
It can be shown that there is a version of s which is jointly Borel measurable, that is
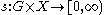
is Borel measurable and satisfies
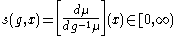
for almost all values of (g, x) ∈ G × X.
Suppose H is a separable Hilbert space, U(H) the unitary operators on H. A unitary cocycle is a Borel mapping

such that
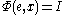
for almost all x ∈ X
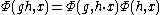
for almost all (g, h, x). A unitary cocycle is strict if and only if the above relations hold for all (g, h, x). It can be shown that for any unitary cocycle there is a strict unitary cocycle which is equal almost everywhere to it (Varadarajan, 1985).
Theorem. Define

Then U is a unitary representation of G on the Hilbert space
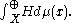
Moreover, if for any Borel set A, π(A) is the projection operator
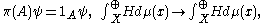
then (U, π) is a system of imprimitivity of (G,X).
Conversely, any homogeneous system of imprimitivity is of this form, for some measure σ-finite measure μ. This measure is unique up to measure equivalence, that is to say, two such measures have the same sets of measure 0.
Indeed much more can be said about the correspondence between homogeneous systems of imprimitivity and cocycles.
When the action of G on X is transitive however, the correspondence takes a particularly explicit form based on the representation obtained by restricting the cocycle Φ to a fixed point subgroup of the action. We consider this case in the next section.
If (U, π) is irreducible, then π is homogeneous. Moreover, the corresponding measure on X as per the previous theorem is ergodic.
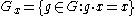
is a closed subgroup of G. Since we are only assuming the action of G on X is Borel, this fact is non-trivial. To prove it, one can use the fact that a standard Borel G-space can be imbedded into a compact G-space in which the action is continuous.
Theorem. Suppose G acts on X transitively. Then there is a σ-finite quasi-invariant measure μ on X which is unique up to measure equivalence (that is any two such measures have the same sets of measure zero).
If Φ is a strict unitary cocycle
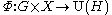
then the restriction of Φ to the fixed point subgroup Gx is a Borel measurable unitary representation U of Gx on H (Here U(H) has the strong operator topology). However, it is known that a Borel measurable unitary representation is equal almost everywhere (with respect to Haar measure) to a strongly continuous unitary representation. This restriction mapping sets up a fundamental correspondence:
Theorem. Suppose G acts on X transitively with quasi-invariant measure μ. There is a bijection from unitary equivalence classes of systems of imprimitivity of (G, X) and unitary equivalence classes of representation of Gx.
Moreover, this bijection preserves irreducibility, that is a system of imprimitivity of (G, X) is irreducible if and only if the corresponding representation of Gx is irreducible.
Given a representation V of Gx the corresponding representation of G is called the representation induced by V.
See Theorem 6.2 of (Varadarajan, 1985).
of G and H a subgroup of G such that G = N H and N ∩ H = {e} (with e being the identity element
of G).
An important example of this is the inhomogeneous Lorentz group
.
Fix G, H and N as above and let X be the character space of N. In particular, H acts on X by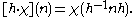
Theorem. There is a bijection between unitary equivalence classes of representations of G and unitary equivalence classes of systems of imprimitivity based on (H, X). This correspondence preserves intertwining operators. In particular, a representation of G is irreducible if and only if the corresponding system of imprimitivity is irreducible.
This result is of particular interest when the action of H on X is such that every ergodic quasi-invariant measure on X is transitive. In that case, each such measure is the image of
(a totally finite version) of Haar measure on X by the map
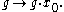
A necessary condition for this to be the case is that there is a countable set of H invariant Borel sets which separate the orbits of H. This is the case for instance for the action of the Lorentz group on the character space of R4.
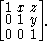
This group is the semi-direct product of
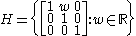
and the abelian normal subgroup
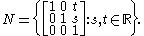
Denote the typical matrix in H by [w] and the typical one in N by [s,t]. Then
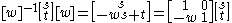
w acts on the dual of R2 by multiplication by the transpose matrix
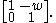
This allows us to completely determine the orbits and the representation theory.
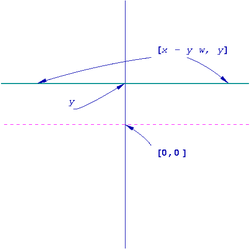
Orbit structure: The orbits fall into two classes:
 Fixed point subgroups: These also fall into two classes depending on the orbit:
Fixed point subgroups: These also fall into two classes depending on the orbit:
Classification: This allows us to completely classify all irreducible representations of the Heisenberg group. These are parametrized by the set consisting of
We can write down explicit formulas for these representations by describing the restrictions to N and H.
Case (1). The corresponding representation π is of the form: It acts on L2(R) with respect to Lebesgue measure and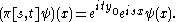
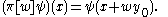
Case (2). The corresponding representation is given by the 1-dimensional character

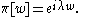
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, both within the context of the theory
Theory
The English word theory was derived from a technical term in Ancient Greek philosophy. The word theoria, , meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action...
of group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s. It was used by George Mackey
George Mackey
George Whitelaw Mackey was an American mathematician. Mackey earned his bachelor of arts at Rice University in 1938 and obtained his Ph.D. at Harvard University in 1942 under the direction of Marshall H. Stone...
as the basis for his theory of induced unitary representation
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
s of locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
s.
The simplest case, and the context in which the idea was first noticed, is that of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s (see primitive permutation group
Primitive permutation group
In mathematics, a permutation group G acting on a set X is called primitive if G acts transitively on X and G preserves no nontrivial partition of X...
). Consider a group G and subgroups H and K, with K contained in H. Then the left coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of H in G are each the union of left cosets of K. Not only that, but translation (on one side) by any element g of G respects this decomposition. The connection with induced representation
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
s is that the permutation representation on cosets is the special case of induced representation, in which a representation is induced from a trivial representation
Trivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
. The structure, combinatorial in this case, respected by translation shows that either K is a maximal subgroup
Maximal subgroup
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
of G, or there is a system of imprimitivity (roughly, a lack of full 'mixing'). In order to generalise this to other cases, the concept is re-expressed: first in terms of functions on G constant on K-cosets, and then in terms of projection operators (for example the averaging over K-cosets of elements of the group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
).
Mackey also used the idea for his explication of quantization theory based on preservation of relativity groups acting on configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
. This generalized work of Eugene Wigner and others and is often considered to be one of the pioneering ideas in canonical quantization
Canonical quantization
In physics, canonical quantization is a procedure for quantizing a classical theory while attempting to preserve the formal structure of the classical theory, to the extent possible. Historically, this was Werner Heisenberg's route to obtaining quantum mechanics...
.
Illustrative example
To motivate the general definitions, we first formulate a definition in the case of finite groups and representations of these on finite dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s.
Suppose G is a finite group and U is a representation of G on a finite-dimensional complex vector space H. The action of G on elements of H induces an action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on the vector subspaces of H in an obvious way:
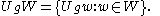
Suppose X is a set of subspaces of H such that (1) X is permuted by the action of G on subspaces and (2) H is the (internal) algebraic direct sum of the spaces in X, written

Then (U, X) is a system of imprimitivity for G.
Two assertions must hold in the above definition:
- the spaces W for W ∈ X must spanLinear spanIn the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
H and - the spaces W ∈ X must be linearly independent, that is the linear relation
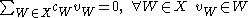
only holds when all the coefficients cW are zero.
If the action of G on the elements of X is transitive, then we say this is a transitive system of imprimitivity.
Suppose G is a finite group, G0 a subgroup of G. A representation U of G is induced from a representation V of G0 if and only if there exist the following:
- a transitive system of imprimitivity (U, X) and
- a subspace W0 ∈ X
such that G0 is the fixed point subgroup of W under the action of G, i.e.
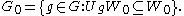
and V is equivalent to the representation of G0
on W0 given by Uh | W0 for h ∈ G0. Note that by this definition, induced by is a relation between representations. We would like to show that there is actually a mapping on representations which corresponds to this relation.
For finite groups one can easily show that a well-defined
Well-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
inducing construction exists on equivalence of representations by considering the character
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
of a representation U defined by
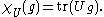
In fact if a representation U of G is induced from a representation V of G0, then
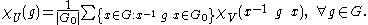
Thus the character function χU (and therefore U itself) is completely determined by χV.
Example
Let G be a finite group and consider the space H of complex-valued functions on G. The left regular representationRegular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
of G on H is defined by
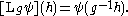
Now H can be considered as the algebraic direct sum of the one dimensional spaces Wx, for x ∈ G, where
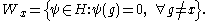
The spaces Wx are permuted by Lg.
Infinite dimensional systems of imprimitivity
To generalize the finite dimensional definition given in the preceding section, a suitable replacement for the set X of vector subspaces of H which is permuted by the representation U is needed. As it turns out, a naïve approach base on subspaces of H will not work; for example the translation representation of R on L2(R) has no system of imprimitivity in this sense. The right formulation of direct sum decomposition is formulated in terms of projection-valued measureProjection-valued measure
In mathematics, particularly functional analysis a projection-valued measure is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a Hilbert space...
s.
Mackey's original formulation was expressed in terms of a locally compact second countable (lcsc) group G, a standard Borel space X and a Borel group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
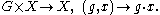
We will refer to this as a standard Borel G-space.
The definitions can be given in a much more general context, but the original setup used by Mackey is still quite general and requires fewer technicalities.
Definition. Let G be a lcsc group acting on a standard Borel space X. A system of imprimitivity based on (G, X) consists of a separable Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H and a pair consisting of
- A strongly-continuous unitary representationUnitary representationIn mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
U: g → Ug of G on H. - A projection-valued measureProjection-valued measureIn mathematics, particularly functional analysis a projection-valued measure is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a Hilbert space...
π on the Borel sets of X with values in the projections of H;
which satisfy
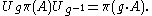
Example
Let X be a standard G space and μ a σ-finite countably additive invariant measure on X. This means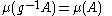
for all g ∈ G and Borel subsets A of G.
Let π(A) be multiplication by the indicator function of A and Ug be the operator
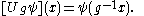
Then (U, π) is a system of imprimitivity of (G, X) on L2μ(X).
This system of imprimitivity is sometimes called the Koopman system of imprimitivity.
Homogeneous systems of imprimitivity
A system of imprimitivity is homogeneous of multiplicity n, where 1 ≤ n ≤ ω if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the corresponding projection-valued measure π on X is homogeneous of multiplicity n. In fact, X breaks up into a countable disjoint family {Xn} 1 ≤ n ≤ ω of Borel sets such that π is homogeneous of multiplicity n on Xn. It is also easy to show Xn is G invariant.
Lemma. Any system of imprimitivity is an orthogonal direct sum of homogeneous ones.
It can be shown that if the action of G on X is transitive, then any system of imprimitivity on X is homogeneous. More generally, if the action of G on X is ergodic (meaning that X cannot be reduced by invariant proper Borel sets of X) then any system of imprimitivity on X is homogeneous.
We now discuss how the structure of homogeneous systems of imprimitivity can be expressed in a form which generalizes the Koopman representation given in the example above.
In the following, we assume that μ is a σ-finite measure on a standard Borel G-space X such that the action of G respects the measure class of μ. This condition is weaker than invariance, but it suffices to construct a unitary translation operator similar to the Koopman operator in the example above. G respects the measure class of μ means that the Radon-Nikodym derivative
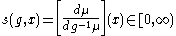
is well-defined for every g ∈ G, where
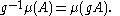
It can be shown that there is a version of s which is jointly Borel measurable, that is
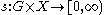
is Borel measurable and satisfies
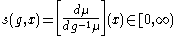
for almost all values of (g, x) ∈ G × X.
Suppose H is a separable Hilbert space, U(H) the unitary operators on H. A unitary cocycle is a Borel mapping

such that
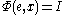
for almost all x ∈ X
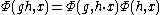
for almost all (g, h, x). A unitary cocycle is strict if and only if the above relations hold for all (g, h, x). It can be shown that for any unitary cocycle there is a strict unitary cocycle which is equal almost everywhere to it (Varadarajan, 1985).
Theorem. Define

Then U is a unitary representation of G on the Hilbert space
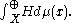
Moreover, if for any Borel set A, π(A) is the projection operator
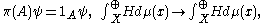
then (U, π) is a system of imprimitivity of (G,X).
Conversely, any homogeneous system of imprimitivity is of this form, for some measure σ-finite measure μ. This measure is unique up to measure equivalence, that is to say, two such measures have the same sets of measure 0.
Indeed much more can be said about the correspondence between homogeneous systems of imprimitivity and cocycles.
When the action of G on X is transitive however, the correspondence takes a particularly explicit form based on the representation obtained by restricting the cocycle Φ to a fixed point subgroup of the action. We consider this case in the next section.
Example
A system of imprimitivity (U, π) of (G,X) on a separable Hilbert space H is irreducible if and only if the only closed subspaces invariant under all the operators Ug and π(A) for g and element of G and A a Borel subset of X are H or {0}.If (U, π) is irreducible, then π is homogeneous. Moreover, the corresponding measure on X as per the previous theorem is ergodic.
Induced representations
If X is a Borel G space and x ∈ X, then the fixed point subgroup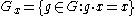
is a closed subgroup of G. Since we are only assuming the action of G on X is Borel, this fact is non-trivial. To prove it, one can use the fact that a standard Borel G-space can be imbedded into a compact G-space in which the action is continuous.
Theorem. Suppose G acts on X transitively. Then there is a σ-finite quasi-invariant measure μ on X which is unique up to measure equivalence (that is any two such measures have the same sets of measure zero).
If Φ is a strict unitary cocycle
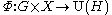
then the restriction of Φ to the fixed point subgroup Gx is a Borel measurable unitary representation U of Gx on H (Here U(H) has the strong operator topology). However, it is known that a Borel measurable unitary representation is equal almost everywhere (with respect to Haar measure) to a strongly continuous unitary representation. This restriction mapping sets up a fundamental correspondence:
Theorem. Suppose G acts on X transitively with quasi-invariant measure μ. There is a bijection from unitary equivalence classes of systems of imprimitivity of (G, X) and unitary equivalence classes of representation of Gx.
Moreover, this bijection preserves irreducibility, that is a system of imprimitivity of (G, X) is irreducible if and only if the corresponding representation of Gx is irreducible.
Given a representation V of Gx the corresponding representation of G is called the representation induced by V.
See Theorem 6.2 of (Varadarajan, 1985).
Applications to the theory of group representations
Systems of imprimitivity arise naturally in the determination of the representations of a group G which is the semi-direct product of an abelian group N by a group H that acts by automorphisms of N. This means N is a normal subgroupNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G and H a subgroup of G such that G = N H and N ∩ H = {e} (with e being the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of G).
An important example of this is the inhomogeneous Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
.
Fix G, H and N as above and let X be the character space of N. In particular, H acts on X by
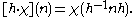
Theorem. There is a bijection between unitary equivalence classes of representations of G and unitary equivalence classes of systems of imprimitivity based on (H, X). This correspondence preserves intertwining operators. In particular, a representation of G is irreducible if and only if the corresponding system of imprimitivity is irreducible.
This result is of particular interest when the action of H on X is such that every ergodic quasi-invariant measure on X is transitive. In that case, each such measure is the image of
(a totally finite version) of Haar measure on X by the map
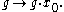
A necessary condition for this to be the case is that there is a countable set of H invariant Borel sets which separate the orbits of H. This is the case for instance for the action of the Lorentz group on the character space of R4.
Example: the Heisenberg group
The Heisenberg group is the group of 3 × 3 real matrices of the form: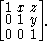
This group is the semi-direct product of
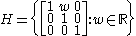
and the abelian normal subgroup
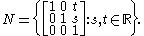
Denote the typical matrix in H by [w] and the typical one in N by [s,t]. Then
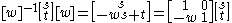
w acts on the dual of R2 by multiplication by the transpose matrix
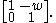
This allows us to completely determine the orbits and the representation theory.
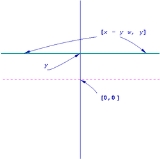
Orbit structure: The orbits fall into two classes:
- A horizontal line which intersects the y-axis at a non-zero value y0. In this case, we can take the quasi-invariant measure on this line to be Lebesgue measure.
- A single point (x0,0) on the x-axis.

- The trivial subgroup {0}.
- The group H itself.
Classification: This allows us to completely classify all irreducible representations of the Heisenberg group. These are parametrized by the set consisting of
- R − {0}. These are infinite-dimensional.
- Pairs (x0, λ) ∈ R × R. x0 is the abscissa of the single point orbit on the x-axis and λ is an element of the dual of H These are one-dimensional.
We can write down explicit formulas for these representations by describing the restrictions to N and H.
Case (1). The corresponding representation π is of the form: It acts on L2(R) with respect to Lebesgue measure and
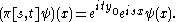
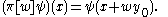
Case (2). The corresponding representation is given by the 1-dimensional character