Supersingular prime (for an elliptic curve)
Encyclopedia
In algebraic number theory
, a supersingular prime is a certain type of prime number
. If E is an elliptic curve
defined over the rational number
s, then a prime
p is supersingular for E if the reduction of E modulo p is a supersingular elliptic curve over the residue field
Fp.
Noam Elkies
showed that any elliptic curve over the rational numbers has infinitely many supersingular primes. However, the set of supersingular primes has asymptotic density zero. In 1976, Lang and Trotter conjectured that the number of supersingular primes less than a bound X is within a constant multiple of X1/2 /(log X), using heuristics involving the distribution of Frobenius eigenvalues. As of 2010, this conjecture is open.
More generally, if K is any global field
— i.e., a finite extension either of Q or of
Fp(t) — and A is an abelian variety
defined over K, then a supersingular prime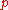
for A is a finite place of K such that the reduction of A modulo 
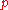is a supersingular abelian variety
.
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, a supersingular prime is a certain type of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. If E is an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
defined over the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, then a prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p is supersingular for E if the reduction of E modulo p is a supersingular elliptic curve over the residue field
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
Fp.
Noam Elkies
Noam Elkies
Noam David Elkies is an American mathematician and chess master.At age 14, Elkies received a gold medal with a perfect score at the International Mathematical Olympiad, the youngest ever to do so...
showed that any elliptic curve over the rational numbers has infinitely many supersingular primes. However, the set of supersingular primes has asymptotic density zero. In 1976, Lang and Trotter conjectured that the number of supersingular primes less than a bound X is within a constant multiple of X1/2 /(log X), using heuristics involving the distribution of Frobenius eigenvalues. As of 2010, this conjecture is open.
More generally, if K is any global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
— i.e., a finite extension either of Q or of
Fp(t) — and A is an abelian variety
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
defined over K, then a supersingular prime
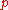for A is a finite place of K such that the reduction of A modulo 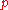is a supersingular abelian varietyAbelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
.