Suffix tree
Encyclopedia
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a suffix tree (also called PAT tree or, in an earlier form, position tree) is a data structure that presents the suffixes of a given string
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
in a way that allows for a particularly fast implementation of many important string operations.
The suffix tree for a string
is a treeTree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
whose edges are labeled with strings, such that each suffix of
corresponds to exactly one path from the tree's root to a leaf. It is thus a radix treeRadix tree
In computer science, a radix tree is a space-optimized trie data structure where each node with only one child is merged with its child. The result is that every internal node has at least two children. Unlike in regular tries, edges can be labeled with sequences of characters as well as single...
(more specifically, a Patricia tree) for the suffixes of
.Constructing such a tree for the string
takes time and space linear in the length of 
. Once constructed, several operations can be performed quickly, for instance locating a substringSubstring
A subsequence, substring, prefix or suffix of a string is a subset of the symbols in a string, where the order of the elements is preserved...
in
, locating a substring if a certain number of mistakes are allowed, locating matches for a regular expressionRegular expression
In computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
pattern etc. Suffix trees also provided one of the first linear-time solutions for the longest common substring problem
Longest common substring problem
The longest common substring problem is to find the longest string that is a substring of two or more strings. It should not be confused with the longest common subsequence problem. The longest common substring problem is to find the longest string (or strings) that is a substring (or are...
. These speedups come at a cost: storing a string's suffix tree typically requires significantly more space than storing the string itself.
History
The concept was first introduced as a position tree by Weiner in 1973, which Donald KnuthDonald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
subsequently characterized as "Algorithm of the Year 1973". The construction was greatly simplified by McCreight in 1976
, and also by Ukkonen in 1995. Ukkonen provided the first online-construction of suffix trees, now known as Ukkonen's algorithm
Ukkonen's algorithm
In 1995, Esko Ukkonen proposed a linear-time, online algorithm for constructing suffix trees that has come to be known as Ukkonen's algorithm.The algorithm begins with an implicit suffix tree containing the first character of the string. Then it steps through the string adding successive characters...
, with running time that matched the then fastest algorithms.
These algorithms are all linear-time for constant-size alphabet, and have worst-case running time of
in general.In 1997, Martin Farach gave the first suffix tree construction algorithm that is optimal for all alphabets. In particular, this is the first linear-time algorithm
for strings drawn from an alphabet of integers in a polynomial range. This latter algorithm has become the basis for new algorithms for constructing both suffix trees and suffix array
Suffix array
In computer science, a suffix array is an array of integers giving the starting positions of suffixes of a string in lexicographical order.-Details:Consider the string...
s, for example, in external memory, compressed, succinct, etc.
Definition
The suffix tree for the string
of length 
is defined as a tree such that ( page 90):
- the paths from the root to the leaves have a one-to-one relationship with the suffixes of
, - edges spell non-empty strings,
- and all internal nodes (except perhaps the root) have at least two children.
Since such a tree does not exist for all strings,
is padded with a terminal symbol not seen in the string (usually denoted $). This ensures that no suffix is a prefix of another, and that there will be 
leaf nodes, one for each of the 
suffixes of 
. Since all internal non-root nodes are branching, there can be at most n − 1 such nodes, and n + (n − 1) + 1 = 2n nodes in total (n leaves, n − 1 internal nodes, 1 root).Suffix links are a key feature for older linear-time construction algorithms, although most newer algorithms, which are based on Farach's algorithm, dispense with suffix links. In a complete suffix tree, all internal non-root nodes have a suffix link to another internal node. If the path from the root to a node spells the string
, where 
is a single character and 
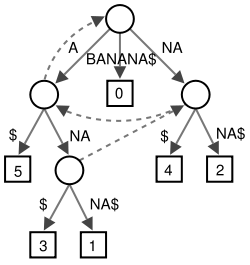
is a string (possibly empty), it has a suffix link to the internal node representing 
. See for example the suffix link from the node for ANA to the node for NA in the figure above. Suffix links are also used in some algorithms running on the tree.Generalised suffix tree
Generalised suffix treeGeneralised suffix tree
A generalised suffix tree is a suffix tree for a set of strings. Given the set of strings D=S_1,S_2,\dots,S_d of total length n, it is a Patricia tree containing all n suffixes of the strings...
is a suffix tree made for a set of words instead only for a single word. It represents all suffixes from this set of words. Each word must be terminated by a different termination symbol or word.
Functionality
A suffix tree for a string
of length 
can be built in 
time, if the letters come from an alphabet of integers in a polynomial range (in particular, this is true for constant-sized alphabets).For larger alphabets, the running time is dominated by first sorting
Sorting algorithm
In computer science, a sorting algorithm is an algorithm that puts elements of a list in a certain order. The most-used orders are numerical order and lexicographical order...
the letters to bring them into a range of size
; in general, this takes 
time.The costs below are given under the assumption that the alphabet is constant.
Assume that a suffix tree has been built for the string
of length 
, or that a generalised suffix treeGeneralised suffix tree
A generalised suffix tree is a suffix tree for a set of strings. Given the set of strings D=S_1,S_2,\dots,S_d of total length n, it is a Patricia tree containing all n suffixes of the strings...
has been built for the set of strings
of total length 
.You can:
- Search for strings:
- Check if a string
of length 
is a substring in 
time ( page 92). - Find the first occurrence of the patterns
of total length 
as substrings in 
time. - Find all
occurrences of the patterns 
of total length 
as substrings in 
time ( page 123).
- Check if a string
-
- Search for a regular expressionRegular expressionIn computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
P in time expected sublinear in
. - Find for each suffix of a pattern
, the length of the longest match between a prefix of 
and a substring in 
in 
time ( page 132). This is termed the matching statistics for 
.
- Search for a regular expression
- Find properties of the strings:
- Find the longest common substringsLongest common substring problemThe longest common substring problem is to find the longest string that is a substring of two or more strings. It should not be confused with the longest common subsequence problem. The longest common substring problem is to find the longest string (or strings) that is a substring (or are...
of the string
and 
in 
time ( page 125). - Find all maximal pairMaximal pairGiven a string S of length n, a maximal pair is a tuple , such that S[p_1..p_1+l-1]=S[p_2..p_2+l-1], but S[p_1-1] \neq S[p_2-1] and S[p_1+l] \neq S[p_2+l]. A maximal repeat is a string represented by such tuple. A supermaximal repeat is a maximal repeat never occurring as a proper substring of...
s, maximal repeats or supermaximal repeats in
time ( page 144). - Find the Lempel–Ziv decomposition in
time ( page 166). - Find the longest repeated substringsLongest repeated substring problemThe longest repeated substring problem is finding the longest substring of a string that occurs at least twice. This problem can be solved in linear time and space by building a suffix tree for the string, and finding the deepest internal node in the tree. The string spelled by the edges from the...
in
time. - Find the most frequently occurring substrings of a minimum length in
time. - Find the shortest strings from
that do not occur in 
, in 
time, if there are 
such strings. - Find the shortest substrings occurring only once in
time. - Find, for each
, the shortest substrings of 
not occurring elsewhere in 
in 
time.
- Find the longest common substrings
The suffix tree can be prepared for constant time lowest common ancestor
Lowest common ancestor
The lowest common ancestor is a concept in graph theory and computer science. Let T be a rooted tree with n nodes. The lowest common ancestor is defined between two nodes v and w as the lowest node in T that has both v and w as descendants .The LCA of v and w in T is the shared ancestor of v...
retrieval between nodes in
time ( chapter 8). You can then also:
- Find the longest common prefix between the suffixes
and 
in 
( page 196). - Search for a pattern P of length m with at most k mismatches in
time, where z is the number of hits ( page 200). - Find all
maximal palindromePalindromeA palindrome is a word, phrase, number, or other sequence of units that can be read the same way in either direction, with general allowances for adjustments to punctuation and word dividers....
s in
( page 198), or 
time if gaps of length 
are allowed, or 
if 
mismatches are allowed ( page 201). - Find all
tandem repeats in 
, and k-mismatch tandem repeats in 
( page 204). - Find the longest substrings commonLongest common substring problemThe longest common substring problem is to find the longest string that is a substring of two or more strings. It should not be confused with the longest common subsequence problem. The longest common substring problem is to find the longest string (or strings) that is a substring (or are...
to at least
strings in 
for 
in 
time ( page 205). - Find the longest palindromic substringLongest palindromic substringIn computer science, the longest palindromic substring or longest symmetric factor problem is the problem of finding a maximum-length contiguous substring of a given string that is also a palindrome. For example, the longest palindromic substring of "bananas" is "anana"...
of a given string (using the suffix trees of both the string and its reverse) in linear time ( pages 197–199).
Applications
Suffix trees can be used to solve a large number of string problems that occur in text-editing, free-text search, computational biology and other application areas. Primary applications include:- String search, in O(m) complexity, where m is the length of the sub-string (but with initial O(n) time required to build the suffix tree for the string)
- Finding the longest repeated substring
- Finding the longest common substring
- Finding the longest palindromePalindromeA palindrome is a word, phrase, number, or other sequence of units that can be read the same way in either direction, with general allowances for adjustments to punctuation and word dividers....
in a string
Suffix trees are often used in bioinformatics
Bioinformatics
Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
applications, searching for patterns in DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
or protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
sequences (which can be viewed as long strings of characters). The ability to search efficiently with mismatches might be considered their greatest strength. Suffix trees are also used in data compression
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
; they can be used to find repeated data, and can be used for the sorting stage of the Burrows–Wheeler transform. Variants of the LZW
LZW
Lempel–Ziv–Welch is a universal lossless data compression algorithm created by Abraham Lempel, Jacob Ziv, and Terry Welch. It was published by Welch in 1984 as an improved implementation of the LZ78 algorithm published by Lempel and Ziv in 1978...
compression schemes use suffix trees (LZSS
LZSS
Lempel-Ziv-Storer-Szymanski is a lossless data compression algorithm, a derivative of LZ77, that was created in 1982 by James Storer and Thomas Szymanski. LZSS was described in article "Data compression via textual substitution" published in Journal of the ACM .LZSS is a dictionary encoding...
). A suffix tree is also used in suffix tree clustering, a data clustering
Data clustering
Cluster analysis or clustering is the task of assigning a set of objects into groups so that the objects in the same cluster are more similar to each other than to those in other clusters....
algorithm used in some search engines (first introduced in ).
Implementation
If each node and edge can be represented in
space, the entire tree can be represented in 
space. The total length of all the strings on all of the edges in the tree is 
, but each edge can be stored as the position and length of a substring of S, giving a total space usage of 
computer words. The worst-case space usage of a suffix tree is seen with a fibonacci wordFibonacci word
thumb|350px|Characterization by a [[cutting sequence]] with a line of slope 1/\varphi or \varphi-1, with \varphi the [[golden ratio]].A Fibonacci word is a specific sequence of binary digits...
, giving the full
nodes.An important choice when making a suffix tree implementation is the parent-child relationships between nodes. The most common is using linked list
Linked list
In computer science, a linked list is a data structure consisting of a group of nodes which together represent a sequence. Under the simplest form, each node is composed of a datum and a reference to the next node in the sequence; more complex variants add additional links...
s called sibling lists. Each node has a pointer to its first child, and to the next node in the child list it is a part of. Hash maps, sorted/unsorted arrays (with array doubling
Dynamic array
In computer science, a dynamic array, growable array, resizable array, dynamic table, or array list is a random access, variable-size list data structure that allows elements to be added or removed...
), and balanced search tree
Self-balancing binary search tree
In computer science, a self-balancing binary search tree is any node based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions....
s may also be used, giving different running time properties. We are interested in:
- The cost of finding the child on a given character.
- The cost of inserting a child.
- The cost of enlisting all children of a node (divided by the number of children in the table below).
Let
be the size of the alphabet. Then you have the following costs:| Lookup | Insertion | Traversal | |
|---|---|---|---|
| Sibling lists / unsorted arrays |  |
 |
 |
| Hash maps |  |
 |
 |
| Balanced search tree |  |
 |
 |
| Sorted arrays |  |
 |
 |
| Hash maps + sibling lists |  |
 |
 |
Note that the insertion cost is amortised, and that the costs for hashing are given perfect hashing.
The large amount of information in each edge and node makes the suffix tree very expensive, consuming about ten to twenty times the memory size of the source text in good implementations. The suffix array
Suffix array
In computer science, a suffix array is an array of integers giving the starting positions of suffixes of a string in lexicographical order.-Details:Consider the string...
reduces this requirement to a factor of four, and researchers have continued to find smaller indexing structures.
External construction
Suffix trees quickly outgrow the main memory on standard machinesfor sequence collections in the order of gigabytes. As such, their
construction
calls for external memory approaches.
There are theoretical results for constructing suffix trees in external
memory.
The algorithm by Farach et al.
is theoretically optimal, with an I/O complexity equal to that of sorting.
However, as discussed for example in,
the overall intricacy of this algorithm has prevented, so far, its
practical implementation.
On the other hand, there have been practical works for constructing
disk-based suffix trees
which scale to (few) GB/hours.
The state of the art methods are TDD,
TRELLIS
,
DiGeST,
and
B2ST
.
TDD and TRELLIS scale up to the entire human genome – approximately 3GB – resulting in a disk-based suffix tree of a size in the tens of gigabytes,. However, these methods cannot handle efficiently collections of sequences exceeding 3GB. DiGeST performs significantly better and is able to handle collections of sequences in the order of 6GB in about 6 hours. The source code and documentation for the latter is available from
.
All these methods can efficiently build suffix trees for the case when the
tree does not fit in main memory,
but the input does.
The most recent method, B2ST, scales to handle
inputs that do not fit in main memory. ERA is a recent parallel suffix tree construction method that is significantly faster. ERA can index the entire human genome in 19 minutes on an 8-core desktop computer with 16GB RAM. On a simple Linux cluster with 16 nodes (4GB RAM per node), ERA can index the entire human genome in less than 9 minutes.
External links
- Suffix Trees by Sartaj SahniSartaj SahniProf. Sartaj Kumar Sahni is an Indian computer scientist, now based in the USA, and is one of the pioneers in the field of data structures. He is a distinguished professor in the Department of Computer and Information Science and Engineering at the University of Florida.- Biography :Sahni received...
- Suffix Trees by Lloyd Allison
- NIST's Dictionary of Algorithms and Data Structures: Suffix Tree
- suffix_tree ANSI C implementation of a Suffix Tree
- libstree, a generic suffix tree library written in C
- Tree::Suffix, a Perl binding to libstree
- Strmat a faster generic suffix tree library written in C (uses arrays instead of linked lists)
- SuffixTree a Python binding to Strmat
- Universal Data Compression Based on the Burrows-Wheeler Transformation: Theory and Practice, application of suffix trees in the BWT
- Theory and Practice of Succinct Data Structures, C++ implementation of a compressed suffix tree]
- Practical Algorithm Template Library, a C++ library with suffix tree implementation on PATRICIA trie, by Roman S. Klyujkov
- A Java implementation