
Sturm's theorem
Encyclopedia
In mathematics
, Sturm's theorem is a symbolic procedure to determine the number of distinct real
roots of a polynomial
. It was named for Jacques Charles François Sturm. Whereas the fundamental theorem of algebra
readily yields the number of complex roots of a polynomial, counted according to their multiplicities, Sturm's theorem deals with real roots only and disregards their multiplicities.
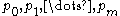
of decreasing degree
with these following properties:
To obtain a Sturm chain, Sturm himself proposed to choose the intermediary results when applying Euclid's algorithm to p and its derivative
:
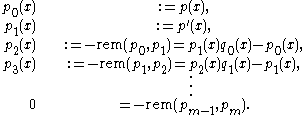
That is, successively take the remainders with polynomial division and change their signs. Since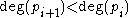 for
for  , the algorithm terminates. The final polynomial, pm, is the greatest common divisor
, the algorithm terminates. The final polynomial, pm, is the greatest common divisor
of p and its derivative. If p is square free, it shares no roots with its derivative, hence pm will be a non-zero constant polynomial. The Sturm chain, called the canonical Sturm chain, then is
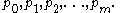
If p is not square-free, this sequence does not formally satisfy the definition of a Sturm chain above, nevertheless it still satisfies the conclusion of Sturm's theorem (see below).
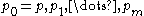 be a Sturm chain, where p is a square-free polynomial, and let σ(ξ) denote the number of sign changes (zeroes are not counted) in the sequence
be a Sturm chain, where p is a square-free polynomial, and let σ(ξ) denote the number of sign changes (zeroes are not counted) in the sequence
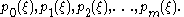
Sturm's theorem then states that for two real numbers a < b, the number of distinct roots of p in the half-open interval (a,b] is σ(a) − σ(b).
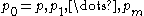 be the canonical Sturm sequence of a polynomial p, not necessarily square-free. Then σ(a) − σ(b) is the number of distinct roots of p in (a,b] whenever a < b are real numbers such that neither a nor b is a multiple root of p.
be the canonical Sturm sequence of a polynomial p, not necessarily square-free. Then σ(a) − σ(b) is the number of distinct roots of p in (a,b] whenever a < b are real numbers such that neither a nor b is a multiple root of p.
s, and any sign change must occur at a root, so consider the behavior of a Sturm chain around the roots of its constituent polynomials.
First, note that two adjacent polynomials can share a common root only when it is a multiple root of p (in which case it is a root of every pi). Indeed, if pi and pi−1 are both zero at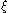 , then pi+1 also have to be zero at
, then pi+1 also have to be zero at 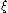 , since
, since 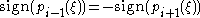 . The zero then propagates recursively up and down the chain, so that
. The zero then propagates recursively up and down the chain, so that 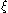 is a root of all the polynomials p0, ..., pm.
is a root of all the polynomials p0, ..., pm.
Next, consider roots of polynomials in the interior (i.e.,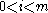 ) of the Sturm chain that are not multiple roots of p. If
) of the Sturm chain that are not multiple roots of p. If 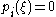 , then we know from the previous paragraph that
, then we know from the previous paragraph that 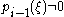 and
and 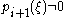 . Furthermore,
. Furthermore, 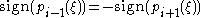 , so in the vicinity of
, so in the vicinity of 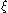 we've got a single sign change across pi−1, pi, pi+1. In other words, sign changes in the interior of the Sturm chain do not affect the total number of sign changes across the chain.
we've got a single sign change across pi−1, pi, pi+1. In other words, sign changes in the interior of the Sturm chain do not affect the total number of sign changes across the chain.
So only roots of the original polynomial, at the top of the chain, can affect the total number of sign changes. Consider a root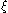 , so
, so 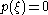 , and assume first that it is a simple root. Then ps derivative, which is p1, must be non-zero at
, and assume first that it is a simple root. Then ps derivative, which is p1, must be non-zero at 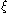 , so p must be either increasing or decreasing at
, so p must be either increasing or decreasing at 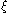 . If it's increasing, then its sign is changing from negative to positive as we move from left to right while its derivative (again, p1) is positive, so the total number of sign changes decreases by one. Conversely, if it's decreasing, then its sign changes from positive to negative while its derivative is negative, so again the total number of sign changes decreases by one.
. If it's increasing, then its sign is changing from negative to positive as we move from left to right while its derivative (again, p1) is positive, so the total number of sign changes decreases by one. Conversely, if it's decreasing, then its sign changes from positive to negative while its derivative is negative, so again the total number of sign changes decreases by one.
Finally, let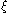 be a multiple root of p, and let p0, ..., pm be the canonical Sturm chain. Let d = gcd(p,p), q = p/d, and let q0, ..., qm be the canonical Sturm chain of q. Then m = m and pi = qid for every i. In particular, σ(x) is the same for both chains whenever x is not a root of d. Then the number of sign changes (in either chain) around
be a multiple root of p, and let p0, ..., pm be the canonical Sturm chain. Let d = gcd(p,p), q = p/d, and let q0, ..., qm be the canonical Sturm chain of q. Then m = m and pi = qid for every i. In particular, σ(x) is the same for both chains whenever x is not a root of d. Then the number of sign changes (in either chain) around 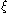 decreases by one, since
decreases by one, since 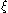 is a simple root of q.
is a simple root of q.
In summary, only sign changes at roots of the original polynomial affect the total number of sign changes across the chain, and the total number of sign changes always decreases by one as we pass a root. The theorem follows directly.
says that all real roots of a polynomial with coefficients ai are in the interval [−M, M], where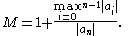
Alternatively, we can use the fact that for large x, the sign of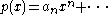
is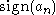 , whereas
, whereas 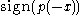 is
is 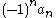 .
.
In this way, simply counting the sign changes in the leading coefficients in the Sturm chain readily gives the number of distinct real roots of a polynomial.
We can also determine the multiplicity of a given root, say ξ, with the help of Sturm's theorem. Indeed, suppose we know a and b bracketing ξ, with σ(a) − σ(b) = 1. Then, ξ has multiplicity k precisely when ξ is a root with multiplicity k − 1 of pm (since it is the GCD of p and its derivative).
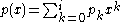 and
and 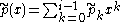 this is accomplished (for non-vanishing
this is accomplished (for non-vanishing 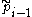 ) by
) by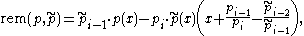
where the quotient is built solely of the first two leading coefficients.
One can check that each Sturm chain is indeed a generalized Sturm chain.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Sturm's theorem is a symbolic procedure to determine the number of distinct real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
roots of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
. It was named for Jacques Charles François Sturm. Whereas the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
readily yields the number of complex roots of a polynomial, counted according to their multiplicities, Sturm's theorem deals with real roots only and disregards their multiplicities.
Sturm chains
A Sturm chain or Sturm sequence is a finite sequence of polynomials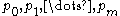
of decreasing degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
with these following properties:
-
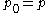 is square freeSquare-free polynomialIn mathematics, a square-free polynomial is a polynomial with no square factors, i.e, f \in F[x] is square-free if and only if b^2 \nmid f for every b \in F[x] with non-zero degree. This definition implies that no factors of higher order can exist, either, for if b3 divided the polynomial, then b2...
is square freeSquare-free polynomialIn mathematics, a square-free polynomial is a polynomial with no square factors, i.e, f \in F[x] is square-free if and only if b^2 \nmid f for every b \in F[x] with non-zero degree. This definition implies that no factors of higher order can exist, either, for if b3 divided the polynomial, then b2...
(no square factors, i.e., no repeated roots); - if
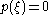 , then
, then 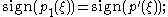
- if
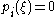 for
for 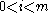 then
then 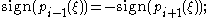
-
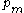 does not change its sign.
does not change its sign.
To obtain a Sturm chain, Sturm himself proposed to choose the intermediary results when applying Euclid's algorithm to p and its derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
:
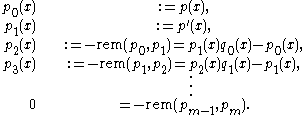
That is, successively take the remainders with polynomial division and change their signs. Since
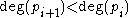 for
for 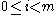 , the algorithm terminates. The final polynomial, pm, is the greatest common divisor
, the algorithm terminates. The final polynomial, pm, is the greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of p and its derivative. If p is square free, it shares no roots with its derivative, hence pm will be a non-zero constant polynomial. The Sturm chain, called the canonical Sturm chain, then is
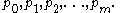
If p is not square-free, this sequence does not formally satisfy the definition of a Sturm chain above, nevertheless it still satisfies the conclusion of Sturm's theorem (see below).
Statement
Let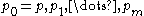 be a Sturm chain, where p is a square-free polynomial, and let σ(ξ) denote the number of sign changes (zeroes are not counted) in the sequence
be a Sturm chain, where p is a square-free polynomial, and let σ(ξ) denote the number of sign changes (zeroes are not counted) in the sequence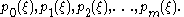
Sturm's theorem then states that for two real numbers a < b, the number of distinct roots of p in the half-open interval (a,b] is σ(a) − σ(b).
The non-square-free case
Let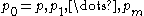 be the canonical Sturm sequence of a polynomial p, not necessarily square-free. Then σ(a) − σ(b) is the number of distinct roots of p in (a,b] whenever a < b are real numbers such that neither a nor b is a multiple root of p.
be the canonical Sturm sequence of a polynomial p, not necessarily square-free. Then σ(a) − σ(b) is the number of distinct roots of p in (a,b] whenever a < b are real numbers such that neither a nor b is a multiple root of p.Proof
Polynomials are continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s, and any sign change must occur at a root, so consider the behavior of a Sturm chain around the roots of its constituent polynomials.
First, note that two adjacent polynomials can share a common root only when it is a multiple root of p (in which case it is a root of every pi). Indeed, if pi and pi−1 are both zero at
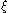 , then pi+1 also have to be zero at
, then pi+1 also have to be zero at 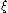 , since
, since 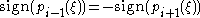 . The zero then propagates recursively up and down the chain, so that
. The zero then propagates recursively up and down the chain, so that 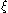 is a root of all the polynomials p0, ..., pm.
is a root of all the polynomials p0, ..., pm.Next, consider roots of polynomials in the interior (i.e.,
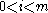 ) of the Sturm chain that are not multiple roots of p. If
) of the Sturm chain that are not multiple roots of p. If 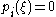 , then we know from the previous paragraph that
, then we know from the previous paragraph that 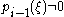 and
and 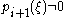 . Furthermore,
. Furthermore, 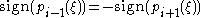 , so in the vicinity of
, so in the vicinity of 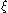 we've got a single sign change across pi−1, pi, pi+1. In other words, sign changes in the interior of the Sturm chain do not affect the total number of sign changes across the chain.
we've got a single sign change across pi−1, pi, pi+1. In other words, sign changes in the interior of the Sturm chain do not affect the total number of sign changes across the chain.So only roots of the original polynomial, at the top of the chain, can affect the total number of sign changes. Consider a root
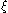 , so
, so 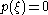 , and assume first that it is a simple root. Then ps derivative, which is p1, must be non-zero at
, and assume first that it is a simple root. Then ps derivative, which is p1, must be non-zero at 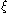 , so p must be either increasing or decreasing at
, so p must be either increasing or decreasing at 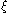 . If it's increasing, then its sign is changing from negative to positive as we move from left to right while its derivative (again, p1) is positive, so the total number of sign changes decreases by one. Conversely, if it's decreasing, then its sign changes from positive to negative while its derivative is negative, so again the total number of sign changes decreases by one.
. If it's increasing, then its sign is changing from negative to positive as we move from left to right while its derivative (again, p1) is positive, so the total number of sign changes decreases by one. Conversely, if it's decreasing, then its sign changes from positive to negative while its derivative is negative, so again the total number of sign changes decreases by one.Finally, let
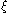 be a multiple root of p, and let p0, ..., pm be the canonical Sturm chain. Let d = gcd(p,p), q = p/d, and let q0, ..., qm be the canonical Sturm chain of q. Then m = m and pi = qid for every i. In particular, σ(x) is the same for both chains whenever x is not a root of d. Then the number of sign changes (in either chain) around
be a multiple root of p, and let p0, ..., pm be the canonical Sturm chain. Let d = gcd(p,p), q = p/d, and let q0, ..., qm be the canonical Sturm chain of q. Then m = m and pi = qid for every i. In particular, σ(x) is the same for both chains whenever x is not a root of d. Then the number of sign changes (in either chain) around 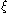 decreases by one, since
decreases by one, since 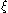 is a simple root of q.
is a simple root of q.In summary, only sign changes at roots of the original polynomial affect the total number of sign changes across the chain, and the total number of sign changes always decreases by one as we pass a root. The theorem follows directly.
Bounds
This can be used to compute the total number of real roots a polynomial has (to use, for example, as an input to a numerical root finder) by choosing a and b appropriately. For example, a bound due to CauchyAugustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
says that all real roots of a polynomial with coefficients ai are in the interval [−M, M], where
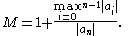
Alternatively, we can use the fact that for large x, the sign of
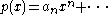
is
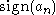 , whereas
, whereas 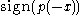 is
is 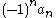 .
.In this way, simply counting the sign changes in the leading coefficients in the Sturm chain readily gives the number of distinct real roots of a polynomial.
We can also determine the multiplicity of a given root, say ξ, with the help of Sturm's theorem. Indeed, suppose we know a and b bracketing ξ, with σ(a) − σ(b) = 1. Then, ξ has multiplicity k precisely when ξ is a root with multiplicity k − 1 of pm (since it is the GCD of p and its derivative).
Quotient
The remainder is needed to compute the chain using Euclid's algorithm. For two polynomials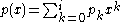 and
and 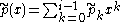 this is accomplished (for non-vanishing
this is accomplished (for non-vanishing 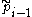 ) by
) by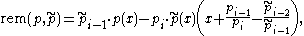
where the quotient is built solely of the first two leading coefficients.
Generalized Sturm chains
Let ξ be in the compact interval [a,b]. A generalized Sturm chain over [a,b] is a finite sequence of real polynomials (X0,X1,…,Xr) such that:- X(a)X(b) ≠ 0
- sign(Xr) is constant on [a,b]
- If Xi(ξ) = 0 for 1 ≤ i ≤ r−1, then Xi−1(ξ)Xi+1(ξ) < 0.
One can check that each Sturm chain is indeed a generalized Sturm chain.
See also
- Routh–Hurwitz theoremRouth–Hurwitz theoremIn mathematics, Routh–Hurwitz theorem gives a test to determine whether a given polynomial is Hurwitz-stable. It was proved in 1895 and named after Edward John Routh and Adolf Hurwitz.-Notations:...
- Hurwitz's theorem (complex analysis)Hurwitz's theorem (complex analysis)In complex analysis, a field within mathematics, Hurwitz's theorem, named after Adolf Hurwitz, roughly states that, under certain conditions, if a sequence of holomorphic functions converges uniformly to a holomorphic function on compact sets, then after a while those functions and the limit...
- Descartes' rule of signsDescartes' rule of signsIn mathematics, Descartes' rule of signs, first described by René Descartes in his work La Géométrie, is a technique for determining the number of positive or negative real roots of a polynomial....
- Rouché's theoremRouché's theoremRouché's theorem, named after , states that if the complex-valued functions f and g are holomorphic inside and on some closed contour K, with |g| ...
- Properties of polynomial roots
- Gauss–Lucas theorem
- Turán's inequalitiesTurán's inequalitiesIn mathematics, Turán's inequalities are some inequalities for Legendre polynomials found by . There are many generalizations to other polynomials, often called Turán's inequalities, given by and other authors....
- D.G. Hook and P.R. McAree, "Using Sturm Sequences To Bracket Real Roots of Polynomial Equations" in Graphic Gems I (A. Glassner ed.), Academic Press, p. 416–422, 1990.
External links
- C code from Graphic Gems by D.G. Hook and P.R. McAree.

