
Stone method
Encyclopedia
Stone's method, also known as the strongly implicit procedure or SIP, is an algorithm
for solving a sparse
linear system of equations. The method uses an incomplete LU decomposition
, which approximates the exact LU decomposition
, to get an iterative
solution of the problem. The method is named after Herbert L. Stone, who proposed it in 1968.
The LU decomposition is an excellent general purpose linear equation solver. The biggest disadvantage is that it fails to take advantage of coefficient matrix to be a sparse matrix. The LU decomposition of a sparse matrix is usually not sparse, thus, for large system of equations, LU decomposition may require a prohibitive amount of memory and arithmetical operations.
In the preconditioned iterative methods, if the preconditioner matrix M is a good approximation of coefficient matrix A then the convergence is faster. This brings us to idea of using approximate factorization LU of A as the iteration matrix M.
A version of incomplete lower-upper decomposition method was proposed by H. L. Stone in 1968. This method is designed for equation system arising from discretisation of partial differential equations and was firstly used for a pentadiagonal system of equation obtained while solving an elliptic
partial differential equation
in a two dimensional space by a finite difference
method. The LU approximate decomposition was looked in the same pentadiagonal form as the original matrix (three diagonal for L and three diagonals for U) as the best match of the seven possible equations for the five unknowns for the each row of the matrix.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for solving a sparse
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
linear system of equations. The method uses an incomplete LU decomposition
Incomplete LU factorization
In numerical analysis, a field within mathematics, an incomplete LU factorization of a matrix is an sparse approximation of the LU factorization. Incomplete LU factorization is often used as a preconditioner.-External links:*...
, which approximates the exact LU decomposition
LU decomposition
In linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
, to get an iterative
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
solution of the problem. The method is named after Herbert L. Stone, who proposed it in 1968.
The LU decomposition is an excellent general purpose linear equation solver. The biggest disadvantage is that it fails to take advantage of coefficient matrix to be a sparse matrix. The LU decomposition of a sparse matrix is usually not sparse, thus, for large system of equations, LU decomposition may require a prohibitive amount of memory and arithmetical operations.
In the preconditioned iterative methods, if the preconditioner matrix M is a good approximation of coefficient matrix A then the convergence is faster. This brings us to idea of using approximate factorization LU of A as the iteration matrix M.
A version of incomplete lower-upper decomposition method was proposed by H. L. Stone in 1968. This method is designed for equation system arising from discretisation of partial differential equations and was firstly used for a pentadiagonal system of equation obtained while solving an elliptic
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
in a two dimensional space by a finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
method. The LU approximate decomposition was looked in the same pentadiagonal form as the original matrix (three diagonal for L and three diagonals for U) as the best match of the seven possible equations for the five unknowns for the each row of the matrix.
Algorithm
- For the linear system Ax = b
- calculate Incomplete LU factorization of matrix A
- Ax = (M-N)x = (LU-N)x = b
- Mx(k+1) = Nx(k)+b , with ||M|| >> ||N||
- Mx(k+1) = LUx(k+1) = c(k)
- LUx(k) = L(Ux(k+1)) = Ly(k) = c(k)
- Ax = (M-N)x = (LU-N)x = b
- set a guess
- k = 0, x(k)
- r(k)=b - Ax(k)
- k = 0, x(k)
- while ( ||r(k)||2
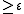 ) do
) do
- evaluate new right hand side
- c(k) = Nx(k) + b
- c(k) = Nx(k) + b
- solve Ly(k) = c(k) by forward substitution
- y(k) = L-1c(k)
- y(k) = L-1c(k)
- solve Ux(k+1) = y(k) by back substitution
- x(k+1) = U-1y(k)
- x(k+1) = U-1y(k)
- evaluate new right hand side
- end while

