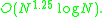Stokesian dynamics
Encyclopedia
Stokesian dynamics
is a solution technique for the Langevin equation
, which is the relevant form of Newton's 2nd law
for a Brownian particle
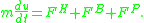
In the above equation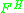
is the hydrodynamic force, i.e., force exerted by the fluid on the particle due to relative motion between them. 
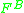is the stochastic
Brownian
force due to thermal motion of fluid particles.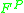
is the inter particle force,e.g. electrostatic repulsion between like charged particles. Brownian dynamics is one of the popular techniques of solving the Langevin equation
, but the hydrodynamic interaction in Brownian dynamics is highly simplified and normally includes only the isolated body resistance. On the other hand, Stokesian dynamics includes the many body hydrodynamic interactions. Hydrodynamic interaction is very important for non-equilibrium suspensions, like a sheared suspension
, where it plays a vital role in its microstructure and hence its properties. Stokesian dynamics is used primarily for non-equilibrium suspensions where it has been shown to provide results which agree with experiments.
) for a large number of particles. Classical Stokesian dynamics requires
operations where N is the number of particles in the system (usually a periodic box). Recent advances have reduced the computational cost to 
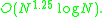
is a solution technique for the Langevin equation
Langevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
, which is the relevant form of Newton's 2nd law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
for a Brownian particle
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
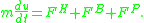
In the above equation
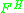is the hydrodynamic force, i.e., force exerted by the fluid on the particle due to relative motion between them. 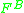is the stochasticStochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
Brownian
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
force due to thermal motion of fluid particles.
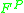is the inter particle force,e.g. electrostatic repulsion between like charged particles. Brownian dynamics is one of the popular techniques of solving the Langevin equationLangevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
, but the hydrodynamic interaction in Brownian dynamics is highly simplified and normally includes only the isolated body resistance. On the other hand, Stokesian dynamics includes the many body hydrodynamic interactions. Hydrodynamic interaction is very important for non-equilibrium suspensions, like a sheared suspension
Suspension (chemistry)
In chemistry, a suspension is a heterogeneous fluid containing solid particles that are sufficiently large for sedimentation. Usually they must be larger than 1 micrometer. The internal phase is dispersed throughout the external phase through mechanical agitation, with the use of certain...
, where it plays a vital role in its microstructure and hence its properties. Stokesian dynamics is used primarily for non-equilibrium suspensions where it has been shown to provide results which agree with experiments.
Hydrodynamic interaction
One of the key features of Stokesian dynamics is its handing of the hydrodynamic interactions, which is fairly accurate without being computationally inhibitive (like boundary integral methodsBoundary element method
The boundary element method is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations . It can be applied in many areas of engineering and science including fluid mechanics, acoustics, electromagnetics, and fracture...
) for a large number of particles. Classical Stokesian dynamics requires
operations where N is the number of particles in the system (usually a periodic box). Recent advances have reduced the computational cost to