
Lah number
Encyclopedia
In mathematics
, Lah numbers, discovered by Ivo Lah
in 1955, are coefficient
s expressing rising factorials in terms of falling factorials.
Unsigned Lah numbers have an interesting meaning in combinatorics
: they count the number of ways a set of n elements can be partition
ed into k nonempty linearly ordered subset
s. Lah numbers are related to Stirling number
s.
Unsigned Lah numbers:
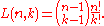
Signed Lah numbers:
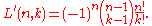
L(n, 1) is always n!; using the interpretation above, the only partition of {1, 2, 3} into 1 set can be ordered in 6 ways:
L(3, 2) corresponds to the 6 partitions with two ordered parts:
L(n, n) is always 1: partitioning {1, 2, 3} into 3 non-empty subsets results in subsets of length 1.
Paraphrasing Karamata-Knuth notation for Stirling numbers, it was
proposed to use the following alternative notation for Lah numbers:
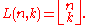
 represent the rising factorial
represent the rising factorial  and let
and let  represent the falling factorial
represent the falling factorial 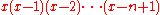 .
.
Then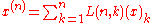 and
and 
For example,
Compare the third row of the table of values.
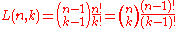


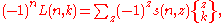 with
with 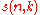 the Stirling numbers of the first kind,
the Stirling numbers of the first kind,  the Stirling numbers of the second kind and with the conventions
the Stirling numbers of the second kind and with the conventions 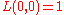 and
and  if
if  .
.
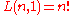
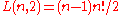
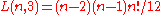
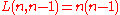
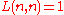
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Lah numbers, discovered by Ivo Lah
Ivo Lah
Ivo Lah was a Slovenian mathematician and actuary, best known for his discovery of the Lah numbers in 1955.Lah attended elementary school in St. Vid nad Cerknico and in Ljubljana...
in 1955, are coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s expressing rising factorials in terms of falling factorials.
Unsigned Lah numbers have an interesting meaning in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
: they count the number of ways a set of n elements can be partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
ed into k nonempty linearly ordered subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s. Lah numbers are related to Stirling number
Stirling number
In mathematics, Stirling numbers arise in a variety of combinatorics problems. They are named after James Stirling, who introduced them in the 18th century. Two different sets of numbers bear this name: the Stirling numbers of the first kind and the Stirling numbers of the second...
s.
Unsigned Lah numbers:
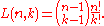
Signed Lah numbers:
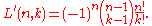
L(n, 1) is always n!; using the interpretation above, the only partition of {1, 2, 3} into 1 set can be ordered in 6 ways:
- {(1, 2, 3)}, {(1, 3, 2)}, {(2, 1, 3)}, {(2, 3, 1)}, {(3, 1, 2)} or {(3, 2, 1)}
L(3, 2) corresponds to the 6 partitions with two ordered parts:
- {(1), (2, 3)}, {(1), (3, 2)}, {(2), (1, 3)}, {(2), (3, 1)}, {(3), (1, 2)} or {(3), (2, 1)}
L(n, n) is always 1: partitioning {1, 2, 3} into 3 non-empty subsets results in subsets of length 1.
- {(1), (2), (3)}
Paraphrasing Karamata-Knuth notation for Stirling numbers, it was
proposed to use the following alternative notation for Lah numbers:
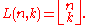
Rising and falling factorials
Let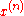 represent the rising factorial
represent the rising factorial  and let
and let  represent the falling factorial
represent the falling factorial 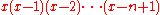 .
.Then
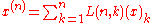 and
and 
For example,

Compare the third row of the table of values.
Identities and relations
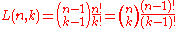


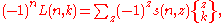 with
with 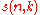 the Stirling numbers of the first kind,
the Stirling numbers of the first kind,  the Stirling numbers of the second kind and with the conventions
the Stirling numbers of the second kind and with the conventions 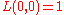 and
and  if
if  .
.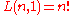
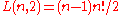
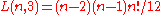
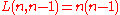
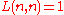
Table of values
Below is a table of values for the Lah numbers:  | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | |||||||||||
| 2 | 2 | 1 | ||||||||||
| 3 | 6 | 6 | 1 | |||||||||
| 4 | 24 | 36 | 12 | 1 | ||||||||
| 5 | 120 | 240 | 120 | 20 | 1 | |||||||
| 6 | 720 | 1800 | 1200 | 300 | 30 | 1 | ||||||
| 7 | 5040 | 15120 | 12600 | 4200 | 630 | 42 | 1 | |||||
| 8 | 40320 | 141120 | 141120 | 58800 | 11760 | 1176 | 56 | 1 | ||||
| 9 | 362880 | 1451520 | 1693440 | 846720 | 211680 | 28224 | 2016 | 72 | 1 | |||
| 10 | 3628800 | 16329600 | 21772800 | 12700800 | 3810240 | 635040 | 60480 | 3240 | 90 | 1 | ||
| 11 | 39916800 | 199584000 | 299376000 | 199584000 | 69854400 | 13970880 | 1663200 | 11880 | 4950 | 110 | 1 | |
| 12 | 479001600 | 2634508800 | 4390848000 | 3293136000 | 1317254400 | 307359360 | 43908480 | 3920400 | 217800 | 7260 | 132 | 1 |

