In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the Steiner inellipse of a triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

 is the unique ellipse

Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

 inscribed in the triangle and tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

 to the sides at their midpoints. It is an example of an inconic. By comparison the inscribed circle of a triangle is another inconic that is tangent to the sides, but not necessarily at the midpoints. The Steiner inellipse is attributed by Dörrie to Jakob Steiner

Jakob Steiner

Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...

, and a proof of its uniqueness is given by Kalman.

Properties

The center of a triangle's Steiner inellipse is the triangle's centroid

Centroid

In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...

 — the intersection of the triangle's median

Median (geometry)

In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians; one running from each vertex to the opposite side...

s.

The Steiner inellipse of a triangle has the largest area of any inellipse of that triangle; the area is 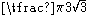times the area of the triangle.

The Steiner inellipse is the only inconic that is tangent at the midpoints of two of the triangle's sides. That is, if an ellipse is tangent to the triangle at two sides' midpoints and also tangent to the third side, then the latter point of tangency is the midpoint of that side.

According to Marden's theorem

Marden's theorem

In mathematics, Marden's theorem, named after Morris Marden, gives a geometric relationship between the zeroes of a third-degree polynomial with complex coefficients and the zeroes of its derivative....

, if the three vertices

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

 of the triangle are the complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

 zeros of a cubic polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

, then the foci

Focus (geometry)

In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...

 of the Steiner inellipse are the zeros of the derivative

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

 of the polynomial.

The major axis of the Steiner inellipse is the line of best orthogonal fit

Deming regression

In statistics, Deming regression, named after W. Edwards Deming, is an errors-in-variables model which tries to find the line of best fit for a two-dimensional dataset...

for the vertices.