
Stability (probability)
Encyclopedia
In probability theory
, the stability of a random variable
is the property that a linear combination of two independent
copies of the variable has the same distribution
, up to location
and scale
parameters. The distributions of random variables having this property are said to be "stable distributions". Results available in probability theory show that all possible distributions having this property are members of a four-parameter family of distributions. The article on the stable distribution describes this family together with some of the properties of these distributions.
The importance in probability theory of "stability" and of the stable family of probability distributions is that they are "attractors" for properly normed sums of independent and identically distributed random variables.
Important special cases of stable distributions are the normal distribution, the Cauchy distribution
and the Lévy distribution. For details see stable distribution.
s.
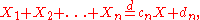
where this equality refers to equality of distributions. A conclusion drawn from this starting point is that the sequence of constants cn must be of the form for
for 
A further conclusion is that it enough for the above distributional identity to hold for n=2 and n=3 only.
are being considered. It is convenient here to call these stable distributions, without meaning specifically the distribution described in the article named stable distribution, or to say that a distribution is stable if it is assumed that it has the stability property. The following results can be obtained for univariate distribution
s which are stable.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the stability of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is the property that a linear combination of two independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
copies of the variable has the same distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, up to location
Location parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
and scale
Scale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
parameters. The distributions of random variables having this property are said to be "stable distributions". Results available in probability theory show that all possible distributions having this property are members of a four-parameter family of distributions. The article on the stable distribution describes this family together with some of the properties of these distributions.
The importance in probability theory of "stability" and of the stable family of probability distributions is that they are "attractors" for properly normed sums of independent and identically distributed random variables.
Important special cases of stable distributions are the normal distribution, the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
and the Lévy distribution. For details see stable distribution.
Definition
There are several basic definitions for what is meant by stability. Some are based on summations of random variables and others on properties of characteristic functionCharacteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
s.
Definition via distribution functions
Feller makes the following basic definition. A random variable X is called stable (has a stable distribution) if, for n independent copies Xi of X, there exist constants cn > 0 and dn such that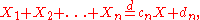
where this equality refers to equality of distributions. A conclusion drawn from this starting point is that the sequence of constants cn must be of the form
 for
for 
A further conclusion is that it enough for the above distributional identity to hold for n=2 and n=3 only.
Stability in probability theory
There are a number of mathematical results that can be derived for distributions which have the stability property. That is, all possible families of distributions which have the property of being closed under convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
are being considered. It is convenient here to call these stable distributions, without meaning specifically the distribution described in the article named stable distribution, or to say that a distribution is stable if it is assumed that it has the stability property. The following results can be obtained for univariate distribution
Univariate distribution
In statistics, a univariate distribution is a probability distribution of only one random variable. This is in contrast to a multivariate distribution, the probability distribution of a random vector.-Further reading:...
s which are stable.
- Stable distributions are always infinitely divisible.
- All stable distributions are absolutely continuous.
- All stable distributions are unimodal.
Other types of stability
The above concept of stability is based on the idea of a class of distributions being closed under a given set of operations on random variables, where the operation is "summation" or "averaging". Other operations that have been considered include:- geometric stability: here the operation is to take the sum of a random number of random variables, where the number has a geometric distribution. The counterpart of the stable distribution in this case is the geometric stable distribution
- Max-stability: here the operation is to take the maximum of a number of random variables. The counterpart of the stable distribution in this case is the generalized extreme value distribution, and the theory for this case is dealt with as extreme value theoryExtreme value theoryExtreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
. See also the stability postulateStability postulateIn probability theory, to obtain a nondegenerate limiting distribution of the extreme value distribution, it is necessary to "reduce" the actual greatest value by applying a linear transformation with coefficients that depend on the sample size....
. A version of this case in which the minimum is taken instead of the maximum is available by a simple extension.

