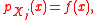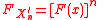Stability postulate
Encyclopedia
In probability theory
, to obtain a nondegenerate limiting distribution of the extreme value distribution, it is necessary to "reduce" the actual greatest value by applying a linear transformation
with coefficients that depend on the sample size.
If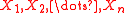 are independent random variable
are independent random variable
s with common probability density function
then the cumulative distribution function
of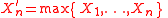 is
is
If there is a limiting distribution of interest, the stability postulate states the limiting distribution is some sequence of transformed "reduced" values, such as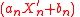 , where
, where 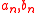 may depend on n but not on x.
may depend on n but not on x.
To distinguish the limiting cumulative distribution function
from the "reduced" greatest value from F(x), we will denote it by G(x). It follows that G(x) must satisfy the functional equation
This equation was obtained by Maurice René Fréchet
and also by Ronald Fisher
.
Boris Vladimirovich Gnedenko
has shown there are no other distributions satisfying the stability postulate other than the following:
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, to obtain a nondegenerate limiting distribution of the extreme value distribution, it is necessary to "reduce" the actual greatest value by applying a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
with coefficients that depend on the sample size.
If
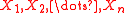 are independent random variable
are independent random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s with common probability density function
then the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of
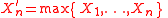 is
isIf there is a limiting distribution of interest, the stability postulate states the limiting distribution is some sequence of transformed "reduced" values, such as
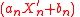 , where
, where 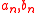 may depend on n but not on x.
may depend on n but not on x.To distinguish the limiting cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
from the "reduced" greatest value from F(x), we will denote it by G(x). It follows that G(x) must satisfy the functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
This equation was obtained by Maurice René Fréchet
Maurice René Fréchet
Maurice Fréchet was a French mathematician. He made major contributions to the topology of point sets and introduced the entire concept of metric spaces. He also made several important contributions to the field of statistics and probability, as well as calculus...
and also by Ronald Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
.
Boris Vladimirovich Gnedenko
Boris Vladimirovich Gnedenko
Boris Vladimirovich Gnedenko was a Soviet mathematician and a student of Andrey Nikolaevich Kolmogorov. He was born in Simbirsk , Russia, and died in Moscow. He is perhaps best known for his work with Kolmogorov, and his contributions to the study of probability theory...
has shown there are no other distributions satisfying the stability postulate other than the following:
- Gumbel distribution for the minimum stability postulate
- If
 and
and 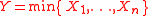 then
then 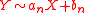 where
where  and
and 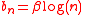
- In other words,
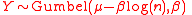
- If
- Extreme value distribution for the maximum stability postulate
- If
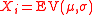 and
and 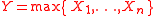 then
then 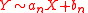 where
where  and
and 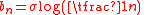
- In other words,

- If
- Fréchet distribution for the maximum stability postulate
- If
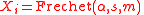 and
and 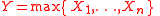 then
then  where
where 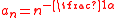 and
and 
- In other words,
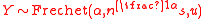
- If