
Specific impulse
Encyclopedia
Specific impulse is a way to describe the efficiency of rocket
and jet
engines. It represents the derivative
of the impulse with respect to amount of propellant
used, i.e., the thrust divided by the amount of propellant used per unit time. If the "amount" of propellant is given in terms of mass
(such as kilograms), then specific impulse has units of velocity
. If it is given in terms of Earth-weight
(such as kiloponds), then specific impulse has units of time. The conversion constant between the two versions of specific impulse is g
. The higher the specific impulse, the lower the propellant flow rate required for a given thrust
, and in the case of a rocket the less propellant is needed for a given delta-v
per the Tsiolkovsky rocket equation.
The actual exhaust velocity is the average speed that the exhaust jet actually leaves the vehicle. The effective exhaust velocity is the speed that the propellant burned per second would have to leave the vehicle to give the same thrust. The two are about the same for a rocket working in a vacuum, but are radically different for an air-breathing jet engine that obtains extra thrust by accelerating air. Specific impulse and effective exhaust velocity are proportional.
Specific impulse is a useful value to compare engines, much like miles per gallon or litres per 100 kilometres is used for cars. A propulsion method with a higher specific impulse is more propellant-efficient. Another number that measures the same thing, usually used for air breathing jet engines, is specific fuel consumption. Specific fuel consumption is inversely proportional to specific impulse and effective exhaust velocity.
shows to be a unit of speed, and so specific impulses are often measured in meters per second and are often termed effective exhaust velocity. However, if propellant weight is used instead, an impulse divided by a force (weight) turns out to be a unit of time, and so specific impulses are measured in seconds. These two formulations are both widely used and differ from each other by a factor of g
, the dimensioned constant
of gravitational acceleration
at the surface of the Earth.
Note that the gain of momentum of a rocket (including fuel) per unit time is not equal to the thrust, because the momentum that the fuel has while in the rocket has to be subtracted to the extent that it is used, i.e., the gain of momentum of a rocket per unit time is equal to the thrust, minus the velocity of the rocket multiplied by the amount of fuel used per unit time. (This gain of momentum of the rocket is the negative of the momentum of the exhaust gas.) See also change of impulse of a variable mass.
The higher the specific impulse, the less propellant is needed to produce a given thrust during a given time. In this regard a propellant is more efficient if the specific impulse is higher. This should not be confused with energy efficiency, which can even decrease as specific impulse increases, since propulsion systems that give high specific impulse require high energy to do so.
In addition it is important that thrust
and specific impulse not be confused with one another. The specific impulse is a measure of the impulse per unit of propellant that is expended, while thrust is a measure of the momentary or peak force supplied by a particular engine. In many cases, propulsion systems with very high specific impulses—some ion thruster
s reach 10,000 seconds—produce low thrusts.
When calculating specific impulse, only propellant that is carried with the vehicle before use is counted. For a chemical rocket the propellant mass therefore would include both fuel and oxidizer; for air-breathing engines only the mass of the fuel is counted, not the mass of air passing through the engine.
By far the most common unit used for specific impulse today is the second, and this is used both in the SI world as well as where English units are used. Its chief advantages are that its units and numerical value are identical everywhere, and essentially everyone understands it. Nearly all manufacturers quote their engine performance in these units and it is also useful for specifying aircraft engine performance.
The effective exhaust velocity in units of m/s is also in reasonably common usage. For rocket engines it is reasonably intuitive, although for many rocket engines the effective exhaust speed is considerably different from the actual exhaust speed due to, for example, fuel and oxidizer that is dumped overboard after powering turbopumps. For airbreathing engines the effective exhaust velocity is not physically meaningful, although it can be used for comparison purposes nevertheless.
The N•s/kg is not uncommonly seen, and is numerically equal to the effective exhaust velocity in m/s (from Newton's second law and the definition of the Newton.)
Another equivalent unit is specific fuel consumption. This has units of g/kN.s or lbf/lb•h and is inversely proportional to specific impulse. Specific fuel consumption is used extensively for describing the performance of air-breathing jet engines.
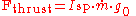
where:
 is the thrust obtained from the engine, in newtons (or poundal
is the thrust obtained from the engine, in newtons (or poundal
s).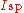 is the specific impulse measured in seconds.
is the specific impulse measured in seconds. is the mass flow rate
is the mass flow rate
in kg/s (lb/s), which is negative the time-rate of change of the vehicle's mass since propellant is being expelled.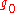 is the acceleration at the Earth's surface, in m/s² (or ft/s²).
is the acceleration at the Earth's surface, in m/s² (or ft/s²).
(When working with English unit
s, it is conventional to divide both sides of the equation by g0 so that the left hand side of the equation has units of lbs rather than expressing it in poundal
s.)
This Isp in seconds value is somewhat physically meaningful—if an engine's thrust could be adjusted to equal the initial weight of its propellant (measured at one standard gravity
), then Isp is the duration the propellant would last.
The advantage that this formulation has is that it may be used for rockets, where all the reaction mass is carried onboard, as well as aeroplanes, where most of the reaction mass is taken from the atmosphere. In addition, it gives a result that is independent of units used (provided the unit of time used is the second).

-on-Earth of the propellant:
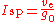
where
Isp is the specific impulse measured in seconds
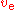 is the average exhaust speed along the axis of the engine in (ft/s or m/s)
is the average exhaust speed along the axis of the engine in (ft/s or m/s)
g0 is the acceleration at the Earth's surface (in ft/s2 or m/s2)
In rockets, due to atmospheric effects, the specific impulse varies with altitude, reaching a maximum in a vacuum.
It is therefore most common to see the specific impulse quoted for the vehicle in a vacuum; the lower sea level values are usually indicated in some way (e.g. 'sl').
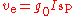
where
 - is the specific impulse in seconds
- is the specific impulse in seconds
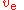 - is the specific impulse measured in m/s
- is the specific impulse measured in m/s
, which is the same as the effective exhaust velocity measured in m/s (or ft/s if g is in ft/s2)
 - is the acceleration due to gravity at the Earth's surface, 9.81 m/s² (in English units units 32.2 ft/s²).
- is the acceleration due to gravity at the Earth's surface, 9.81 m/s² (in English units units 32.2 ft/s²).
This equation is also valid for airbreathing jet engines, but is rarely used in practice.
(Note that different symbols are sometimes used; for example, c is also sometimes seen for exhaust velocity. While the symbol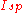 might logically be used for specific impulse in units of N•s/kg, to avoid confusion it is desirable to reserve this for specific impulse measured in seconds.)
might logically be used for specific impulse in units of N•s/kg, to avoid confusion it is desirable to reserve this for specific impulse measured in seconds.)
It is related to the thrust
, or forward force on the rocket by the equation:

where
 is the propellant mass flow rate, which is the rate of decrease of the vehicle's mass
is the propellant mass flow rate, which is the rate of decrease of the vehicle's mass
A rocket must carry all its fuel with it, so the mass of the unburned fuel must be accelerated along with the rocket itself. Minimizing the mass of fuel required to achieve a given push is crucial to building effective rockets. The Tsiolkovsky rocket equation
shows that for a rocket with a given empty mass and a given amount of fuel, the total change in velocity
it can accomplish is proportional to the effective exhaust velocity.
A spacecraft without propulsion follows an orbit determined by the gravitational field. Deviations from the corresponding velocity pattern (these are called Δv) are achieved by sending exhaust mass in the direction opposite to that of the desired velocity change.
For airbreathing jet engines, particularly, turbofan
s, the actual exhaust velocity and the effective exhaust velocity are different by orders of magnitude. This is because a good deal of additional momentum is obtained by using air as reaction mass. This allows for a better match between the airspeed and the exhaust speed which saves energy/propellant and enormously increases the effective exhaust velocity while reducing the actual exhaust velocity.
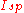 implies lower energy efficiency: the power needed to run the engine is simply:
implies lower energy efficiency: the power needed to run the engine is simply:
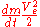
where Ve is the actual jet velocity.
whereas from momentum considerations the thrust generated is:
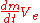
Dividing the power by the thrust to obtain the specific power requirements we get:
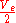
Hence the power needed is proportional to the exhaust velocity, with higher velocities needing higher power for the same thrust, causing less energy efficiency per unit thrust.
However, the total energy for a mission depends on total propellant use, as well as how much energy is needed per unit of propellant. For low exhaust velocity with respect to the mission delta-v, enormous amounts of reaction mass is needed. In fact a very low exhaust velocity is not energy efficient at all for this reason; but it turns out that neither are very high exhaust velocities.
Theoretically, for a given delta-v
, in space, among all fixed values for the exhaust speed the value is the most energy efficient with respect to the final mass, see Tsiolkovsky rocket equation
is the most energy efficient with respect to the final mass, see Tsiolkovsky rocket equation
.
However, a variable exhaust speed can be more energy efficient still. For example, if a rocket is accelerated from some positive initial speed using an exhaust speed equal to the speed of the rocket no energy is lost as kinetic energy of reaction mass, since it becomes stationary. (Theoretically, by making this initial speed low and using another method of obtaining this small speed, the energy efficiency approaches 100%, but requires a large initial mass.) In this case the rocket keeps the same momentum
, so its speed is inversely proportional to its remaining mass. During such a flight the kinetic energy of the rocket is proportional to its speed and, correspondingly, inversely proportional to its remaining mass. The power needed per unit acceleration is constant throughout the flight; the reaction mass to be expelled per unit time to produce a given acceleration is proportional to the square of the rocket's remaining mass.
Also it is advantageous to expel reaction mass at a location where the gravity potential is low, see Oberth effect
.
) both improves energy efficiency as well as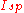 .
.
An example of a specific impulse measured in time is 453 second
s, which is equivalent to an effective exhaust velocity of 4,440 m/s
, for the Space Shuttle Main Engine
s when operating in a vacuum. An air-breathing jet engine typically has a much larger specific impulse than a rocket; for example a turbofan
jet engine may have a specific impulse of 6,000 seconds or more at sea level whereas a rocket would be around 200–400 seconds.
An air-breathing engine is thus much more propellant efficient than a rocket engine, because the actual exhaust speed is much lower, the air provides an oxidizer, and air is used as reaction mass. Since the physical exhaust velocity is lower, the kinetic energy the exhaust carries away is lower and thus the jet engine uses far less energy to generate thrust (at subsonic speeds). While the actual exhaust velocity is lower for air-breathing engines, the effective exhaust velocity is very high for jet engines. This is because the effective exhaust velocity calculation essentially assumes that the propellant is providing all the thrust, and hence is not physically meaningful for air-breathing engines; nevertheless, it is useful for comparison with other types of engines.
The highest specific impulse for a chemical propellant ever test-fired in a rocket engine was 542 seconds (5,320 m/s) with a tripropellant
of lithium, fluorine, and hydrogen. However, this combination is impractical; see rocket fuel.
Nuclear thermal rocket
engines differ from conventional rocket engines in that thrust is created strictly through thermodynamic phenomena, with no chemical reaction. The nuclear rocket typically operates by passing hydrogen gas through a superheated nuclear core. Testing in the 1960s yielded specific impulses of about 850 seconds (8,340 m/s), about twice that of the Space Shuttle engines.
A variety of other non-rocket propulsion methods, such as ion thruster
s, give much higher specific impulse but with much lower thrust; for example the Hall effect thruster
on the SMART-1
satellite has a specific impulse of 1,640 s (16,100 m/s) but a maximum thrust of only 68 millinewtons. The hypothetical Variable specific impulse magnetoplasma rocket
(VASIMR) propulsion would theoretically yield a minimum of 10,000−300,000 m/s but would probably require a great deal of heavy machinery to confine even relatively diffuse plasmas, and so would be unusable for high-thrust applications such as launch from planetary surfaces.
is a large, well-known American seller of model rocket components. The specific impulse for model rocket motors is much lower than for many other rocket motors because the manufacturer uses black powder propellant. The burn rate of model rocket motors is also tightly controlled.
Rocket engine
A rocket engine, or simply "rocket", is a jet engineRocket Propulsion Elements; 7th edition- chapter 1 that uses only propellant mass for forming its high speed propulsive jet. Rocket engines are reaction engines and obtain thrust in accordance with Newton's third law...
and jet
Jet engine
A jet engine is a reaction engine that discharges a fast moving jet to generate thrust by jet propulsion and in accordance with Newton's laws of motion. This broad definition of jet engines includes turbojets, turbofans, rockets, ramjets, pulse jets...
engines. It represents the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the impulse with respect to amount of propellant
Propellant
A propellant is a material that produces pressurized gas that:* can be directed through a nozzle, thereby producing thrust ;...
used, i.e., the thrust divided by the amount of propellant used per unit time. If the "amount" of propellant is given in terms of mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
(such as kilograms), then specific impulse has units of velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
. If it is given in terms of Earth-weight
Weight
In science and engineering, the weight of an object is the force on the object due to gravity. Its magnitude , often denoted by an italic letter W, is the product of the mass m of the object and the magnitude of the local gravitational acceleration g; thus:...
(such as kiloponds), then specific impulse has units of time. The conversion constant between the two versions of specific impulse is g
Standard gravity
Standard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
. The higher the specific impulse, the lower the propellant flow rate required for a given thrust
Thrust
Thrust is a reaction force described quantitatively by Newton's second and third laws. When a system expels or accelerates mass in one direction the accelerated mass will cause a force of equal magnitude but opposite direction on that system....
, and in the case of a rocket the less propellant is needed for a given delta-v
Delta-v
In astrodynamics a Δv or delta-v is a scalar which takes units of speed. It is a measure of the amount of "effort" that is needed to change from one trajectory to another by making an orbital maneuver....
per the Tsiolkovsky rocket equation.
The actual exhaust velocity is the average speed that the exhaust jet actually leaves the vehicle. The effective exhaust velocity is the speed that the propellant burned per second would have to leave the vehicle to give the same thrust. The two are about the same for a rocket working in a vacuum, but are radically different for an air-breathing jet engine that obtains extra thrust by accelerating air. Specific impulse and effective exhaust velocity are proportional.
Specific impulse is a useful value to compare engines, much like miles per gallon or litres per 100 kilometres is used for cars. A propulsion method with a higher specific impulse is more propellant-efficient. Another number that measures the same thing, usually used for air breathing jet engines, is specific fuel consumption. Specific fuel consumption is inversely proportional to specific impulse and effective exhaust velocity.
General considerations
Propellant is normally measured either in units of mass or weight. If mass is used, specific impulse is an impulse per unit mass, which dimensional analysisDimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
shows to be a unit of speed, and so specific impulses are often measured in meters per second and are often termed effective exhaust velocity. However, if propellant weight is used instead, an impulse divided by a force (weight) turns out to be a unit of time, and so specific impulses are measured in seconds. These two formulations are both widely used and differ from each other by a factor of g
Standard gravity
Standard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
, the dimensioned constant
Physical constant
A physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.There are many physical constants in...
of gravitational acceleration
Standard gravity
Standard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
at the surface of the Earth.
Note that the gain of momentum of a rocket (including fuel) per unit time is not equal to the thrust, because the momentum that the fuel has while in the rocket has to be subtracted to the extent that it is used, i.e., the gain of momentum of a rocket per unit time is equal to the thrust, minus the velocity of the rocket multiplied by the amount of fuel used per unit time. (This gain of momentum of the rocket is the negative of the momentum of the exhaust gas.) See also change of impulse of a variable mass.
The higher the specific impulse, the less propellant is needed to produce a given thrust during a given time. In this regard a propellant is more efficient if the specific impulse is higher. This should not be confused with energy efficiency, which can even decrease as specific impulse increases, since propulsion systems that give high specific impulse require high energy to do so.
In addition it is important that thrust
Thrust
Thrust is a reaction force described quantitatively by Newton's second and third laws. When a system expels or accelerates mass in one direction the accelerated mass will cause a force of equal magnitude but opposite direction on that system....
and specific impulse not be confused with one another. The specific impulse is a measure of the impulse per unit of propellant that is expended, while thrust is a measure of the momentary or peak force supplied by a particular engine. In many cases, propulsion systems with very high specific impulses—some ion thruster
Ion thruster
An ion thruster is a form of electric propulsion used for spacecraft propulsion that creates thrust by accelerating ions. Ion thrusters are categorized by how they accelerate the ions, using either electrostatic or electromagnetic force. Electrostatic ion thrusters use the Coulomb force and...
s reach 10,000 seconds—produce low thrusts.
When calculating specific impulse, only propellant that is carried with the vehicle before use is counted. For a chemical rocket the propellant mass therefore would include both fuel and oxidizer; for air-breathing engines only the mass of the fuel is counted, not the mass of air passing through the engine.
Units
| |
Specific Impulse (by weight) |
Specific Impulse (by mass) |
Effective exhaust velocity |
Specific fuel consumption |
|---|---|---|---|---|
| SI | =X seconds | =9.8066 X N•s/kg | =9.8066 X m/s | =(101,972/X) g/kN•s |
| English units | =X seconds | =X lbf•s/lb | =32.16 X ft/s | =(3,600/X) lb/lbf•h |
By far the most common unit used for specific impulse today is the second, and this is used both in the SI world as well as where English units are used. Its chief advantages are that its units and numerical value are identical everywhere, and essentially everyone understands it. Nearly all manufacturers quote their engine performance in these units and it is also useful for specifying aircraft engine performance.
The effective exhaust velocity in units of m/s is also in reasonably common usage. For rocket engines it is reasonably intuitive, although for many rocket engines the effective exhaust speed is considerably different from the actual exhaust speed due to, for example, fuel and oxidizer that is dumped overboard after powering turbopumps. For airbreathing engines the effective exhaust velocity is not physically meaningful, although it can be used for comparison purposes nevertheless.
The N•s/kg is not uncommonly seen, and is numerically equal to the effective exhaust velocity in m/s (from Newton's second law and the definition of the Newton.)
Another equivalent unit is specific fuel consumption. This has units of g/kN.s or lbf/lb•h and is inversely proportional to specific impulse. Specific fuel consumption is used extensively for describing the performance of air-breathing jet engines.
General definition
For all vehicles specific impulse (impulse per unit weight-on-Earth of propellant) in seconds can be defined by the following equation: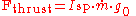
where:
 is the thrust obtained from the engine, in newtons (or poundal
is the thrust obtained from the engine, in newtons (or poundalPoundal
The poundal is a unit of force that is part of the foot-pound-second system of units, in Imperial units introduced in 1877, and is from the specialized subsystem of English Absolut ....
s).
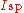 is the specific impulse measured in seconds.
is the specific impulse measured in seconds. is the mass flow rate
is the mass flow rateMass flow rate
Mass flow rate is the mass of substance which passes through a given surface per unit time. Its unit is mass divided by time, so kilogram per second in SI units, and slug per second or pound per second in US customary units...
in kg/s (lb/s), which is negative the time-rate of change of the vehicle's mass since propellant is being expelled.
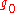 is the acceleration at the Earth's surface, in m/s² (or ft/s²).
is the acceleration at the Earth's surface, in m/s² (or ft/s²).(When working with English unit
English unit
English units are the historical units of measurement used in England up to 1824, which evolved as a combination of the Anglo-Saxon and Roman systems of units...
s, it is conventional to divide both sides of the equation by g0 so that the left hand side of the equation has units of lbs rather than expressing it in poundal
Poundal
The poundal is a unit of force that is part of the foot-pound-second system of units, in Imperial units introduced in 1877, and is from the specialized subsystem of English Absolut ....
s.)
This Isp in seconds value is somewhat physically meaningful—if an engine's thrust could be adjusted to equal the initial weight of its propellant (measured at one standard gravity
Standard gravity
Standard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
), then Isp is the duration the propellant would last.
The advantage that this formulation has is that it may be used for rockets, where all the reaction mass is carried onboard, as well as aeroplanes, where most of the reaction mass is taken from the atmosphere. In addition, it gives a result that is independent of units used (provided the unit of time used is the second).

Rocketry
In rocketry, where the only reaction mass is the propellant, an equivalent way of calculating the specific impulse in seconds is also frequently used. In this sense, specific impulse is defined as the thrust integrated over time per unit weightWeight
In science and engineering, the weight of an object is the force on the object due to gravity. Its magnitude , often denoted by an italic letter W, is the product of the mass m of the object and the magnitude of the local gravitational acceleration g; thus:...
-on-Earth of the propellant:
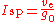
where
Isp is the specific impulse measured in seconds
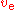 is the average exhaust speed along the axis of the engine in (ft/s or m/s)
is the average exhaust speed along the axis of the engine in (ft/s or m/s)g0 is the acceleration at the Earth's surface (in ft/s2 or m/s2)
In rockets, due to atmospheric effects, the specific impulse varies with altitude, reaching a maximum in a vacuum.
It is therefore most common to see the specific impulse quoted for the vehicle in a vacuum; the lower sea level values are usually indicated in some way (e.g. 'sl').
Specific impulse as a speed (effective exhaust velocity)
Because of the geocentric factor of g0 in the equation for specific impulse, many prefer to define the specific impulse of a rocket (in particular) in terms of thrust per unit mass flow of propellant (instead of per unit weight flow). This is an equally valid (and in some ways somewhat simpler) way of defining the effectiveness of a rocket propellant. For a rocket, the specific impulse defined in this way is simply the effective exhaust velocity relative to the rocket, ve. The two definitions of specific impulse are proportional to one another, and related to each other by: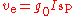
where
 - is the specific impulse in seconds
- is the specific impulse in seconds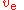 - is the specific impulse measured in m/s
- is the specific impulse measured in m/sMetre per second
Metre per second is an SI derived unit of both speed and velocity , defined by distance in metres divided by time in seconds....
, which is the same as the effective exhaust velocity measured in m/s (or ft/s if g is in ft/s2)
 - is the acceleration due to gravity at the Earth's surface, 9.81 m/s² (in English units units 32.2 ft/s²).
- is the acceleration due to gravity at the Earth's surface, 9.81 m/s² (in English units units 32.2 ft/s²).This equation is also valid for airbreathing jet engines, but is rarely used in practice.
(Note that different symbols are sometimes used; for example, c is also sometimes seen for exhaust velocity. While the symbol
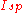 might logically be used for specific impulse in units of N•s/kg, to avoid confusion it is desirable to reserve this for specific impulse measured in seconds.)
might logically be used for specific impulse in units of N•s/kg, to avoid confusion it is desirable to reserve this for specific impulse measured in seconds.)It is related to the thrust
Thrust
Thrust is a reaction force described quantitatively by Newton's second and third laws. When a system expels or accelerates mass in one direction the accelerated mass will cause a force of equal magnitude but opposite direction on that system....
, or forward force on the rocket by the equation:

where
 is the propellant mass flow rate, which is the rate of decrease of the vehicle's mass
is the propellant mass flow rate, which is the rate of decrease of the vehicle's massA rocket must carry all its fuel with it, so the mass of the unburned fuel must be accelerated along with the rocket itself. Minimizing the mass of fuel required to achieve a given push is crucial to building effective rockets. The Tsiolkovsky rocket equation
Tsiolkovsky rocket equation
The Tsiolkovsky rocket equation, or ideal rocket equation is an equation that is useful for considering vehicles that follow the basic principle of a rocket: where a device that can apply acceleration to itself by expelling part of its mass with high speed and moving due to the conservation of...
shows that for a rocket with a given empty mass and a given amount of fuel, the total change in velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
it can accomplish is proportional to the effective exhaust velocity.
A spacecraft without propulsion follows an orbit determined by the gravitational field. Deviations from the corresponding velocity pattern (these are called Δv) are achieved by sending exhaust mass in the direction opposite to that of the desired velocity change.
Actual exhaust speed versus effective exhaust speed
Note that effective exhaust velocity and actual exhaust velocity can be significantly different, for example when a rocket is run within the atmosphere, atmospheric pressure on the outside of the engine causes a retarding force that reduces the specific impulse and the effective exhaust velocity goes down, whereas the actual exhaust velocity is largely unaffected. Also, sometimes rocket engines have a separate nozzle for the turbopump turbine gas, and then calculating the effective exhaust velocity requires averaging the two mass flows as well as accounting for any atmospheric pressure.For airbreathing jet engines, particularly, turbofan
Turbofan
The turbofan is a type of airbreathing jet engine that is widely used for aircraft propulsion. A turbofan combines two types of engines, the turbo portion which is a conventional gas turbine engine, and the fan, a propeller-like ducted fan...
s, the actual exhaust velocity and the effective exhaust velocity are different by orders of magnitude. This is because a good deal of additional momentum is obtained by using air as reaction mass. This allows for a better match between the airspeed and the exhaust speed which saves energy/propellant and enormously increases the effective exhaust velocity while reducing the actual exhaust velocity.
Rockets
For rockets and rocket-like engines such as ion-drives a higher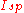 implies lower energy efficiency: the power needed to run the engine is simply:
implies lower energy efficiency: the power needed to run the engine is simply: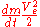
where Ve is the actual jet velocity.
whereas from momentum considerations the thrust generated is:
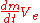
Dividing the power by the thrust to obtain the specific power requirements we get:
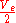
Hence the power needed is proportional to the exhaust velocity, with higher velocities needing higher power for the same thrust, causing less energy efficiency per unit thrust.
However, the total energy for a mission depends on total propellant use, as well as how much energy is needed per unit of propellant. For low exhaust velocity with respect to the mission delta-v, enormous amounts of reaction mass is needed. In fact a very low exhaust velocity is not energy efficient at all for this reason; but it turns out that neither are very high exhaust velocities.
Theoretically, for a given delta-v
Delta-v
In astrodynamics a Δv or delta-v is a scalar which takes units of speed. It is a measure of the amount of "effort" that is needed to change from one trajectory to another by making an orbital maneuver....
, in space, among all fixed values for the exhaust speed the value
 is the most energy efficient with respect to the final mass, see Tsiolkovsky rocket equation
is the most energy efficient with respect to the final mass, see Tsiolkovsky rocket equationTsiolkovsky rocket equation
The Tsiolkovsky rocket equation, or ideal rocket equation is an equation that is useful for considering vehicles that follow the basic principle of a rocket: where a device that can apply acceleration to itself by expelling part of its mass with high speed and moving due to the conservation of...
.
However, a variable exhaust speed can be more energy efficient still. For example, if a rocket is accelerated from some positive initial speed using an exhaust speed equal to the speed of the rocket no energy is lost as kinetic energy of reaction mass, since it becomes stationary. (Theoretically, by making this initial speed low and using another method of obtaining this small speed, the energy efficiency approaches 100%, but requires a large initial mass.) In this case the rocket keeps the same momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, so its speed is inversely proportional to its remaining mass. During such a flight the kinetic energy of the rocket is proportional to its speed and, correspondingly, inversely proportional to its remaining mass. The power needed per unit acceleration is constant throughout the flight; the reaction mass to be expelled per unit time to produce a given acceleration is proportional to the square of the rocket's remaining mass.
Also it is advantageous to expel reaction mass at a location where the gravity potential is low, see Oberth effect
Oberth effect
In astronautics, the Oberth effect is where the use of a rocket engine when travelling at high speed generates much more useful energy than one at low speed...
.
Air breathing
Air-breathing engines such as turbojets increase the momentum generated from their propellant by using it to power the acceleration of inert air rearwards. It turns out that the amount of energy needed to generate a particular amount of thrust is inversely proportional to the amount of air propelled rearwards, thus increasing the mass of air (as with a turbofanTurbofan
The turbofan is a type of airbreathing jet engine that is widely used for aircraft propulsion. A turbofan combines two types of engines, the turbo portion which is a conventional gas turbine engine, and the fan, a propeller-like ducted fan...
) both improves energy efficiency as well as
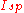 .
.Examples
- For a more complete list see: Spacecraft propulsion#Table of methods
An example of a specific impulse measured in time is 453 second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
s, which is equivalent to an effective exhaust velocity of 4,440 m/s
Metre per second
Metre per second is an SI derived unit of both speed and velocity , defined by distance in metres divided by time in seconds....
, for the Space Shuttle Main Engine
Space Shuttle main engine
The RS-25, otherwise known as the Space Shuttle Main Engine , is a reusable liquid-fuel rocket engine built by Pratt & Whitney Rocketdyne for the Space Shuttle, running on liquid hydrogen and oxygen. Each Space Shuttle was propelled by three SSMEs mated to one powerhead...
s when operating in a vacuum. An air-breathing jet engine typically has a much larger specific impulse than a rocket; for example a turbofan
Turbofan
The turbofan is a type of airbreathing jet engine that is widely used for aircraft propulsion. A turbofan combines two types of engines, the turbo portion which is a conventional gas turbine engine, and the fan, a propeller-like ducted fan...
jet engine may have a specific impulse of 6,000 seconds or more at sea level whereas a rocket would be around 200–400 seconds.
An air-breathing engine is thus much more propellant efficient than a rocket engine, because the actual exhaust speed is much lower, the air provides an oxidizer, and air is used as reaction mass. Since the physical exhaust velocity is lower, the kinetic energy the exhaust carries away is lower and thus the jet engine uses far less energy to generate thrust (at subsonic speeds). While the actual exhaust velocity is lower for air-breathing engines, the effective exhaust velocity is very high for jet engines. This is because the effective exhaust velocity calculation essentially assumes that the propellant is providing all the thrust, and hence is not physically meaningful for air-breathing engines; nevertheless, it is useful for comparison with other types of engines.
The highest specific impulse for a chemical propellant ever test-fired in a rocket engine was 542 seconds (5,320 m/s) with a tripropellant
Tripropellant rocket
A tripropellant rocket is a rocket that uses three propellants, as opposed to the more common bipropellant rocket or monopropellant rocket designs, which use two or one fuels, respectively...
of lithium, fluorine, and hydrogen. However, this combination is impractical; see rocket fuel.
Nuclear thermal rocket
Nuclear thermal rocket
In a nuclear thermal rocket a working fluid, usually liquid hydrogen, is heated to a high temperature in a nuclear reactor, and then expands through a rocket nozzle to create thrust. In this kind of thermal rocket, the nuclear reactor's energy replaces the chemical energy of the propellant's...
engines differ from conventional rocket engines in that thrust is created strictly through thermodynamic phenomena, with no chemical reaction. The nuclear rocket typically operates by passing hydrogen gas through a superheated nuclear core. Testing in the 1960s yielded specific impulses of about 850 seconds (8,340 m/s), about twice that of the Space Shuttle engines.
A variety of other non-rocket propulsion methods, such as ion thruster
Ion thruster
An ion thruster is a form of electric propulsion used for spacecraft propulsion that creates thrust by accelerating ions. Ion thrusters are categorized by how they accelerate the ions, using either electrostatic or electromagnetic force. Electrostatic ion thrusters use the Coulomb force and...
s, give much higher specific impulse but with much lower thrust; for example the Hall effect thruster
Hall effect thruster
In spacecraft propulsion, a Hall thruster is a type of ion thruster in which the propellant is accelerated by an electric field. Hall thrusters trap electrons in a magnetic field and then use the electrons to ionize propellant, efficiently accelerate the ions to produce thrust, and neutralize the...
on the SMART-1
SMART-1
SMART-1 was a Swedish-designed European Space Agency satellite that orbited around the Moon. It was launched on September 27, 2003 at 23:14 UTC from the Guiana Space Centre in Kourou, French Guiana. "SMART" stands for Small Missions for Advanced Research in Technology...
satellite has a specific impulse of 1,640 s (16,100 m/s) but a maximum thrust of only 68 millinewtons. The hypothetical Variable specific impulse magnetoplasma rocket
Variable specific impulse magnetoplasma rocket
The Variable Specific Impulse Magnetoplasma Rocket is an electro-magnetic thruster for spacecraft propulsion. It uses radio waves to ionize and heat a propellant and magnetic fields to accelerate the resulting plasma to generate thrust...
(VASIMR) propulsion would theoretically yield a minimum of 10,000−300,000 m/s but would probably require a great deal of heavy machinery to confine even relatively diffuse plasmas, and so would be unusable for high-thrust applications such as launch from planetary surfaces.
Larger rocket engines
Here are some example numbers for larger rocket engines:Model rocketry
Specific impulse is also used to measure performance in model rocket motors. Following are some of Estes' claimed values for specific impulses for several of their rocket motors: Estes IndustriesEstes Industries
Estes Industries is a company based in Penrose, Colorado, USA that designs and builds model rocket and model aircraft engines and kits. They were the best known model rocket company during the "golden age of rocketry" in the 1970s and early 1980s, competing primarily with Centuri Engineering and a...
is a large, well-known American seller of model rocket components. The specific impulse for model rocket motors is much lower than for many other rocket motors because the manufacturer uses black powder propellant. The burn rate of model rocket motors is also tightly controlled.
| Engine | Total Impulse (Ns) | Fuel Weight (N) | Specific Impulse (s) |
|---|---|---|---|
| Estes A10-3T | 2.5 | .0370 | 67.49 |
| Estes A8-3 | 2.5 | .0306 | 81.76 |
| Estes B4-2 | 5.0 | .0816 | 61.25 |
| Estes B6-4 | 5.0 | .0612 | 81.76 |
| Estes C6-3 | 10 | .1223 | 81.76 |
| Estes C11-5 | 10 | .1078 | 92.76 |
| Estes D12-3 | 20 | .2443 | 81.86 |
| Estes E9-6 | 30 | .3508 | 85.51 |
See also
- Jet engineJet engineA jet engine is a reaction engine that discharges a fast moving jet to generate thrust by jet propulsion and in accordance with Newton's laws of motion. This broad definition of jet engines includes turbojets, turbofans, rockets, ramjets, pulse jets...
- Impulse
- Tsiolkovsky rocket equationTsiolkovsky rocket equationThe Tsiolkovsky rocket equation, or ideal rocket equation is an equation that is useful for considering vehicles that follow the basic principle of a rocket: where a device that can apply acceleration to itself by expelling part of its mass with high speed and moving due to the conservation of...
- System-specific impulseSystem-specific impulseThe term System-specific Impulse, Issp is mostly used to describe the performance of jet propulsion systems. A reference number is introduced, which defines the total impulse, Itot, delivered by the system, divided by the system mass, mPS:...
- Specific energySpecific energySpecific energy is defined as the energy per unit mass. Common metric units are J/kg. It is an intensive property. Contrast this with energy, which is an extensive property. There are two main types of specific energy: potential energy and specific kinetic energy. Others are the gray and sievert,...
- Thrust specific fuel consumption - fuel consumption per unit thrust
- Specific thrustSpecific thrustSpecific thrust is a term used in gas turbine engineering to show the relative bulk of a jet engine and is defined as the ratio: net thrust/total intake airflow.-Low specific thrust engines:...
thrust per unit of air for a duct engine - Heating value
- Energy densityEnergy densityEnergy density is a term used for the amount of energy stored in a given system or region of space per unit volume. Often only the useful or extractable energy is quantified, which is to say that chemically inaccessible energy such as rest mass energy is ignored...
- Delta-v (physics)Delta-v (physics)In general physics, delta-v is simply the change in velocity. The Greek letter delta is a standard mathematical symbol to represent change ....
- Rocket Propulsion Analysis

