
Siacci's theorem
Encyclopedia
In dynamics
, the acceleration
of a particle moving along a curve in space is the time derivative of its velocity. In most applications, the acceleration vector is expressed as the sum of its normal and tangential components
, which are orthogonal to each other. Siacci’s theorem, formulated by the Italian mathematician Francesco Siacci
(1839–1907), is the kinematical decomposition of the acceleration vector into its radial and tangential components. In general, the radial and tangential components are not orthogonal to each other. Siacci’s theorem is particularly useful in motions where the angular momentum
is constant.
(planar motion). Suppose that C is the curve traced out by P and s is the arc length of C corresponding to time t. Let O be an arbitrary origin in the plane and {i,j} be a fixed orthonormal basis
. The position vector of the particle is
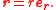
The unit vector er is the radial basis vector of a polar coordinate system
in the plane. The velocity
vector of the particle is

where et is the unit tangent vector to C. Define the angular momentum of P as

where k = i x j. Assume that h ≠ 0. The position vector r may then be expressed as
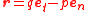
in the Serret-Frenet Basis
{et, en, eb}. The magnitude of the angular momentum h = pv, where p is the perpendicular from the origin to the tangent line ZP. According to Siacci’s theorem, the acceleration a of P can be expressed as
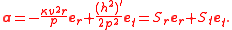
where the prime denotes differentiation with respect to the arc length s, and κ is the curvature
function of the curve C. In general, Sr and St are not equal to the orthogonal projections of a onto er and et.
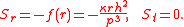
Because the curvature at a point in an orbit is given by
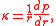
the function f can be written as
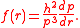
The energy conservation equation for the particle is then obtained if f(r) is integrable.
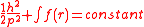 .
.

The tangential component is tangent to the curve C. The radial component is directed from the point P to the point where the perpendicular from an arbitrary fixed origin meets the osculating plane
. Other expressions for a can be found in [1], where a new proof of Siacci's theorem is given.
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
, the acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
of a particle moving along a curve in space is the time derivative of its velocity. In most applications, the acceleration vector is expressed as the sum of its normal and tangential components
Tangential and normal components
In mathematics, given a vector at a point on a curve, that vector can be decomposed uniquely as a sum of two vectors, one tangent to the curve, called the tangential component of the vector, and another one perpendicular to the curve, called the normal component of the vector...
, which are orthogonal to each other. Siacci’s theorem, formulated by the Italian mathematician Francesco Siacci
Francesco Siacci
Francesco Siacci , an Italian mathematician, ballistician, and officer in the Italian army, was born in Rome, Italy. He was a professor of mechanics in the University of Turin and University of Naples...
(1839–1907), is the kinematical decomposition of the acceleration vector into its radial and tangential components. In general, the radial and tangential components are not orthogonal to each other. Siacci’s theorem is particularly useful in motions where the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
is constant.
Siacci's theorem in the plane
Let a particle P of mass m move in a two-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(planar motion). Suppose that C is the curve traced out by P and s is the arc length of C corresponding to time t. Let O be an arbitrary origin in the plane and {i,j} be a fixed orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
. The position vector of the particle is
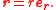
The unit vector er is the radial basis vector of a polar coordinate system
Polar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
in the plane. The velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
vector of the particle is

where et is the unit tangent vector to C. Define the angular momentum of P as

where k = i x j. Assume that h ≠ 0. The position vector r may then be expressed as
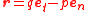
in the Serret-Frenet Basis
Frenet-Serret formulas
In vector calculus, the Frenet–Serret formulas describe the kinematic properties of a particle which moves along a continuous, differentiable curve in three-dimensional Euclidean space R3...
{et, en, eb}. The magnitude of the angular momentum h = pv, where p is the perpendicular from the origin to the tangent line ZP. According to Siacci’s theorem, the acceleration a of P can be expressed as
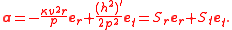
where the prime denotes differentiation with respect to the arc length s, and κ is the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
function of the curve C. In general, Sr and St are not equal to the orthogonal projections of a onto er and et.
Example: Central forces
Suppose that the angular momentum of the particle P is a nonzero constant and that Sr is a function of r. Then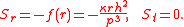
Because the curvature at a point in an orbit is given by
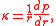
the function f can be written as
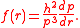
The energy conservation equation for the particle is then obtained if f(r) is integrable.
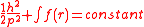 .
.Siacci's theorem in space
Siacci’s theorem can be extended to three-dimensional motions. Thus, let C be a space curve traced out by P and s is the arc length of C corresponding to time t. Also, suppose that the binormal component of the angular momentum does not vanish. Then the acceleration vector of P can be expressed as
The tangential component is tangent to the curve C. The radial component is directed from the point P to the point where the perpendicular from an arbitrary fixed origin meets the osculating plane
Osculating plane
In mathematics, particularly in differential geometry, an osculating plane is a plane in a Euclidean space or affine space which meets a submanifold at a point in such a way as to have a second order of contact at the point. The word osculate is from the Latin osculatus which is a past participle...
. Other expressions for a can be found in [1], where a new proof of Siacci's theorem is given.
See also
- AccelerationAccelerationIn physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
- Areal velocityAreal velocityAreal velocity is the rate at which area is swept out by a particle as it moves along a curve. In many applications, the curve lies in a plane, but in others, it is a space curve....
- Central force
- Serret-Frenet equationsFrenet-Serret formulasIn vector calculus, the Frenet–Serret formulas describe the kinematic properties of a particle which moves along a continuous, differentiable curve in three-dimensional Euclidean space R3...

