Hermitian manifold
Encyclopedia
In mathematics
, a Hermitian manifold is the complex analog of a Riemannian manifold
. Specifically, a Hermitian manifold is a complex manifold
with a smoothly varying Hermitian inner product on each (holomorphic) tangent space
. One can also define a Hermitian manifold as a real manifold with a Riemannian metric that preserves a complex structure.
Complex structure is essentially an almost complex structure with an integrability condition, and this condition yields an unitary structure (U(n) structure
) on the manifold. By dropping this condition we get an almost Hermitian manifold.
On any almost Hermitian manifold we can introduce a fundamental 2-form, or cosymplectic structure, that depends only on the chosen metric and almost complex structure. This form is always non-degenerate, with the suitable integrability condition (of it also being closed and thus a symplectic form) we get an almost Kähler structure. If both almost complex structure and fundamental form are integrable, we have a Kähler structure.
such that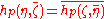
for all ζ, η in Ep and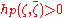
for all nonzero ζ in Ep.
A Hermitian manifold is a complex manifold
with a Hermitian metric on its holomorphic tangent space
. Likewise, an almost Hermitian manifold is an almost complex manifold
with a Hermitian metric on its holomorphic tangent space.
On a Hermitian manifold the metric can be written in local holomorphic coordinates (zα) as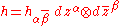
where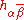
are the components of a positive-definite Hermitian matrix.
The form g is a symmetric bilinear form on TMC, the complexified tangent bundle. Since g is equal to its conjugate it is the complexification of a real form on TM. The symmetry and positive-definiteness of g on TM follow from the corresponding properties of h. In local holomorphic coordinates the metric g can be written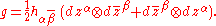
One can also associate to h a complex differential form
ω of degree (1,1). The form ω is defined as minus the imaginary part of h: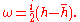
Again since ω is equal to its conjugate it is the complexification of a real form on TM. The form ω is called variously the associated (1,1) form, the fundamental form, or the Hermitian form. In local holomorphic coordinates ω can be written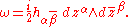
It is clear from the coordinate representations that any one of the three forms h, g, and ω uniquely determine the other two. The Riemannian metric g and associated (1,1) form ω are related by the almost complex structure J as follows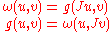
for all complex tangent vectors u and v. The Hermitian metric h can be recovered from g and ω via the identity
All three forms h, g, and ω preserve the almost complex structure J. That is,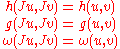
for all complex tangent vectors u and v.
A Hermitian structure on an (almost) complex manifold M can therefore be specified by either
Note that many authors call g itself the Hermitian metric.
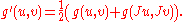
Choosing a Hermitian metric on an almost complex manifold M is equivalent to a choice of U(n)-structure
on M; that is, a reduction of the structure group
of the frame bundle
of M from GL(n,C) to the unitary group
U(n). A unitary frame on an almost Hermitian manifold is complex linear frame which is orthonormal with respect to the Hermitian metric. The unitary frame bundle of M is the principal U(n)-bundle
of all unitary frames.
Every almost Hermitian manifold M has a canonical volume form
which is just the Riemannian volume form determined by g. This form is given in terms of the associated (1,1)-form ω by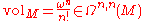
where ωn is the wedge product of ω with itself n times. The volume form is therefore a real (n,n)-form on M. In local holomorphic coordinates the volume form is given by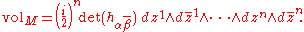
s. These are Hermitian manifolds for which the Hermitian form ω is closed:
In this case the form ω is called a Kähler form. A Kähler form is a symplectic form, and so Kähler manifolds are naturally symplectic manifold
s.
An almost Hermitian manifold whose associated (1,1)-form is closed is naturally called an almost Kähler manifold. Any symplectic manifold admits a compatible almost complex structure making it into an almost Kähler manifold.
Let (M, g, ω, J) be an almost Hermitian manifold of real dimension 2n and let ∇ be the Levi-Civita connection
of g. The following are equivalent conditions for M to be Kähler:
The equivalence of these conditions corresponds to the "2 out of 3" property of the unitary group
.
In particular, if M is a Hermitian manifold, the condition dω = 0 is equivalent to the apparently much stronger conditions ∇ω = ∇J = 0. The richness of Kähler theory is due in part to these properties.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Hermitian manifold is the complex analog of a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. Specifically, a Hermitian manifold is a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
with a smoothly varying Hermitian inner product on each (holomorphic) tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
. One can also define a Hermitian manifold as a real manifold with a Riemannian metric that preserves a complex structure.
Complex structure is essentially an almost complex structure with an integrability condition, and this condition yields an unitary structure (U(n) structure
G-structure
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
) on the manifold. By dropping this condition we get an almost Hermitian manifold.
On any almost Hermitian manifold we can introduce a fundamental 2-form, or cosymplectic structure, that depends only on the chosen metric and almost complex structure. This form is always non-degenerate, with the suitable integrability condition (of it also being closed and thus a symplectic form) we get an almost Kähler structure. If both almost complex structure and fundamental form are integrable, we have a Kähler structure.
Formal definition
A Hermitian metric on a complex vector bundle E over a smooth manifold M is a smoothly varying positive-definite Hermitian form on each fiber. Such a metric can be written as a smooth sectionsuch that
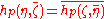
for all ζ, η in Ep and
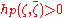
for all nonzero ζ in Ep.
A Hermitian manifold is a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
with a Hermitian metric on its holomorphic tangent space
Holomorphic tangent space
In mathematics, specifically in the field of complex geometry, the holomorphic tangent space of a complex manifold M is the tangent space of the smooth manifold Σ underlying M viewed as complex vector space via the almost complex structure J of M...
. Likewise, an almost Hermitian manifold is an almost complex manifold
Almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
with a Hermitian metric on its holomorphic tangent space.
On a Hermitian manifold the metric can be written in local holomorphic coordinates (zα) as
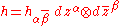
where
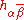are the components of a positive-definite Hermitian matrix.Riemannian metric and associated form
A Hermitian metric h on an (almost) complex manifold M defines a Riemannian metric g on the underlying smooth manifold. The metric g is defined to be the real part of h:The form g is a symmetric bilinear form on TMC, the complexified tangent bundle. Since g is equal to its conjugate it is the complexification of a real form on TM. The symmetry and positive-definiteness of g on TM follow from the corresponding properties of h. In local holomorphic coordinates the metric g can be written
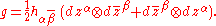
One can also associate to h a complex differential form
Complex differential form
In mathematics, a complex differential form is a differential form on a manifold which is permitted to have complex coefficients....
ω of degree (1,1). The form ω is defined as minus the imaginary part of h:
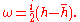
Again since ω is equal to its conjugate it is the complexification of a real form on TM. The form ω is called variously the associated (1,1) form, the fundamental form, or the Hermitian form. In local holomorphic coordinates ω can be written
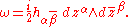
It is clear from the coordinate representations that any one of the three forms h, g, and ω uniquely determine the other two. The Riemannian metric g and associated (1,1) form ω are related by the almost complex structure J as follows
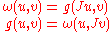
for all complex tangent vectors u and v. The Hermitian metric h can be recovered from g and ω via the identity
All three forms h, g, and ω preserve the almost complex structure J. That is,
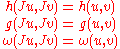
for all complex tangent vectors u and v.
A Hermitian structure on an (almost) complex manifold M can therefore be specified by either
- a Hermitian metric h as above,
- a Riemannian metric g that preserves the almost complex structure J, or
- a nondegenerate 2-form ω which preserves J and is positive-definite in the sense that ω(u, Ju) > 0 for all nonzero real tangent vectors u.
Note that many authors call g itself the Hermitian metric.
Properties
Every (almost) complex manifold admits a Hermitian metric. This follows directly from the analogous statement for Riemannian metric. Given an arbitrary Riemannian metric g on an almost complex manifold M one can construct a new metric g′ compatible with the almost complex structure J in an obvious manner: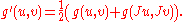Choosing a Hermitian metric on an almost complex manifold M is equivalent to a choice of U(n)-structure
G-structure
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
on M; that is, a reduction of the structure group
Reduction of the structure group
In mathematics, in particular the theory of principal bundles, one can ask if a G-bundle "comes from" a subgroup H In mathematics, in particular the theory of principal bundles, one can ask if a...
of the frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
of M from GL(n,C) to the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n). A unitary frame on an almost Hermitian manifold is complex linear frame which is orthonormal with respect to the Hermitian metric. The unitary frame bundle of M is the principal U(n)-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
of all unitary frames.
Every almost Hermitian manifold M has a canonical volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
which is just the Riemannian volume form determined by g. This form is given in terms of the associated (1,1)-form ω by
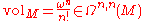
where ωn is the wedge product of ω with itself n times. The volume form is therefore a real (n,n)-form on M. In local holomorphic coordinates the volume form is given by
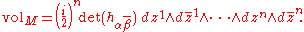
Kähler manifolds
The most important class of Hermitian manifolds are Kähler manifoldKähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
s. These are Hermitian manifolds for which the Hermitian form ω is closed:
In this case the form ω is called a Kähler form. A Kähler form is a symplectic form, and so Kähler manifolds are naturally symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s.
An almost Hermitian manifold whose associated (1,1)-form is closed is naturally called an almost Kähler manifold. Any symplectic manifold admits a compatible almost complex structure making it into an almost Kähler manifold.
Integrability
A Kähler manifold is an almost Hermitian manifold satisfying an integrability condition. This can be stated in several equivalent ways.Let (M, g, ω, J) be an almost Hermitian manifold of real dimension 2n and let ∇ be the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
of g. The following are equivalent conditions for M to be Kähler:
- ω is closed and J is integrable
- ∇J = 0,
- ∇ω = 0,
- the holonomy group of ∇ is contained in the unitary groupUnitary groupIn mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n) associated to J.
The equivalence of these conditions corresponds to the "2 out of 3" property of the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
.
In particular, if M is a Hermitian manifold, the condition dω = 0 is equivalent to the apparently much stronger conditions ∇ω = ∇J = 0. The richness of Kähler theory is due in part to these properties.