
Semiperfect ring
Encyclopedia
In abstract algebra
, a semiperfect ring is a ring
over which every finitely generated left module
has a projective cover
. This property is left right symmetric.
R is semiperfect iff every simple
left R-module
has a projective cover
, every ring
Morita equivalent
to a semiperfect ring is also semiperfect.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a semiperfect ring is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
over which every finitely generated left module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
has a projective cover
Projective cover
In the branch of abstract mathematics called category theory, a projective cover of an object X is in a sense the best approximation of X by a projective object P. Projective covers are the dual of injective envelopes.- Definition :...
. This property is left right symmetric.
Definition
Let R be ring. Then R is semiperfect if any of the following equivalent conditions hold:- R/J(R) is semisimpleSemisimple moduleIn mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring which is a semisimple module over itself is known as an artinian semisimple ring...
and idempotents lift modulo J(R), where J(R) is the Jacobson radicalJacobson radicalIn mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
of R. - R has a complete orthogonal set e1, ..., en of idempotents with each ei R ei a local ringLocal ringIn abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
. - Every simpleSimple moduleIn mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
left (right) R-moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
has a projective coverProjective coverIn the branch of abstract mathematics called category theory, a projective cover of an object X is in a sense the best approximation of X by a projective object P. Projective covers are the dual of injective envelopes.- Definition :...
. - Every finitely generated left (right) R-module has a projective coverProjective coverIn the branch of abstract mathematics called category theory, a projective cover of an object X is in a sense the best approximation of X by a projective object P. Projective covers are the dual of injective envelopes.- Definition :...
. - The category of finitely generated projective
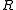 -modules is Krull-Schmidt.
-modules is Krull-Schmidt.
Examples
Examples of semiperfect rings include:- Left (right) perfect ringPerfect ringIn the area of abstract algebra known as ring theory, a left perfect ring is a type of ring in which all left modules have projective covers. The right case is defined by analogy, and the condition is not left-right symmetric, that is, there exist rings which are perfect on one side but not the...
s. - Local ringLocal ringIn abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
s. - Left (right) Artinian ringArtinian ringIn abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
s. - Finite dimensionalDimension (vector space)In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
k-algebrasAlgebra over a fieldIn mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
.
Properties
Since a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R is semiperfect iff every simple
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
left R-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
has a projective cover
Projective cover
In the branch of abstract mathematics called category theory, a projective cover of an object X is in a sense the best approximation of X by a projective object P. Projective covers are the dual of injective envelopes.- Definition :...
, every ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
Morita equivalent
Morita equivalence
In abstract algebra, Morita equivalence is a relationship defined between rings that preserves many ring-theoretic properties. It is named after Japanese mathematician Kiiti Morita who defined equivalence and a similar notion of duality in 1958.- Motivation :...
to a semiperfect ring is also semiperfect.

