Semigroup with two elements
Encyclopedia
In mathematics
, a semigroup with two elements is a semigroup
for which the cardinality of the underlying set is two. There are exactly five distinct nonisomorphic semigroups having two elements:
The semigroups LO2 and RO2 are antiisomorphic
. O2, and are commutative
, LO2 and RO2 are noncommutative. LO2, RO2 and are band
s and also inverse semigroups.
s can be defined in A. These operations are shown in the table below. In the table, a matrix
of the form
indicates a binary operation on A having the following Cayley table
.
In this table:
The two-element semigroup ({0,1},
The Cayley table
for the semigroup ({0,1},
) is given below:
This is the simplest non-trivial example of a semigroup that is not a group. This semigroup is commutative and has an identity element, which is 1 . It is not a group because the element 0 does not have an inverse. In fact, it is not even a cancellative semigroup because we cannot cancel the 0 in the equation 1·0 = 0·0.
This semigroup arises in various contexts. For instance, if we choose 1 to be the truth value "true
" and 0 to be the truth value "false
" and the operation to be the logical connective
"and
", we obtain this semigroup in logic
. It is also isomorphic to the semigroup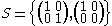
under matrix multiplication
.
for the semigroup (Z2,+2) is given below:
This group is isomorphic to the symmetric group
S2.
Algorithms and computer programs have been developed for determining nonisomorphic finite semigroups of a given order. These have been applied to determine the nonisomorphic semigroups of order three or higher. In fact, 113 of the 19683 binary operations determine 24 nonisomorphic semigroups, or 18 non-equivalent semigroups (with equivalence being isomorphism or anti-isomorphism). The number of nonisomorphic semigroups with n elements, for n a nonnegative integer, is listed under A027851 in the On-Line Encyclopedia of Integer Sequences. A001423 lists the number of non-equivalent semigroups, and A023814 the number of associative binary operations, out of a total of nn2, determining a semigroup.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a semigroup with two elements is a semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
for which the cardinality of the underlying set is two. There are exactly five distinct nonisomorphic semigroups having two elements:
- O2, the null semigroupNull semigroupIn mathematics, a null semigroup is a semigroup with an absorbing element, called zero, in which the product of any two elements is zero...
of order two, - LO2 and RO2, the left zero semigroup of order two and right zero semigroup of order two, respectively,
- ({0,1}, ∧) (where "∧" is the logical connectiveLogical connectiveIn logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
"andLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
"), the non-null semigroup with zero of order two, - (Z2, +2) (where Z2 = {0,1} and "+2" is "addition modulo 2Modular AdditionModular additions are usually side and 2nd story additions to homes that are pre-fabricated at the facilities. General characteristics of a modular home apply. For a 2nd story modular addition the existing house should have a sound structure as modular rooms are 30%+ heavier than the same stick-built...
"): the groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of order two.
The semigroups LO2 and RO2 are antiisomorphic
Antiisomorphic
In modern algebra, an antiisomorphism between structured sets A and B is an isomorphism from A to the opposite of B...
. O2, and are commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, LO2 and RO2 are noncommutative. LO2, RO2 and are band
Band (algebra)
In mathematics, a band is a semigroup in which every element is idempotent . Bands were first studied and named by ; the lattice of varieties of bands was described independently in the early 1970s by Biryukov, Fennemore and Gerhard...
s and also inverse semigroups.
Determination of semigroups with two elements
Choosing the set A = { 1, 2 } as the underlying set having two elements, sixteen binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s can be defined in A. These operations are shown in the table below. In the table, a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of the form
| x | y |
| z | t |
indicates a binary operation on A having the following Cayley table
Cayley table
A Cayley table, after the 19th century British mathematician Arthur Cayley, describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table...
.
| 1 | 2 | |
|---|---|---|
| 1 | x | y |
| 2 | z | t |
EWLINE
|
EWLINE
|
|
EWLINE
|
||||||||||||||||
| Null semigroup O2 | ≡ Semigroup ({0,1},  ) |
2·(1·2) = 2, (2·1)·2 = 1 | Left zero semigroup LO2 | ||||||||||||||||
|
EWLINE
|
EWLINE
|
EWLINE
|
||||||||||||||||
| 2·(1·2) = 1, (2·1)·2 = 2 | Right zero semigroup RO2 | ≡ Group (Z2, +2) | ≡ Semigroup ({0,1},  ) |
||||||||||||||||
|
EWLINE
|
|
|
||||||||||||||||
| 1·(1·2) = 2, (1·1)·2 = 1 | ≡ Group (Z2, +2) | 1·(1·1) = 1, (1·1)·1 = 2 | 1·(2·1) = 1, (1·2)·1 = 2 | ||||||||||||||||
|
|
|
EWLINE
|
||||||||||||||||
| 1·(1·1) = 2, (1·1)·1 = 1 | 1·(2·1) = 2, (1·2)·1 = 1 | 1·(1·2) = 2, (1·1)·2 = 1 | Null semigroup O2 |
In this table:
- The semigroup ({0,1},
) denotes the two-element semigroup containing the zero element 0 and the unit element 1. The two binary operations defined by matrices in a green background are associative and they make A semigroups all of which are isomorphic to the semigroup ({0,1}, 
). - The two binary operations defined by matrices in a blue background are associative and they make A semigroups both of which are isomorphic to the null semigroupNull semigroupIn mathematics, a null semigroup is a semigroup with an absorbing element, called zero, in which the product of any two elements is zero...
O2 with two elements. - The binary operation defined by the matrix in a yellow background is associative and it makes a A semigroup. This is the left zero semigroup LO2.
- The binary operation defined by the matrix in a pink background is associative and it makes A a semigroup. This is the left zero semigroup LO2 and the other is a right zero semigroup RO2.
- The two binary operations defined by matrices in a brown background are associative and they make A semigroups both of which are isomorphic to the groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(Z2, +2). - The remaining eight binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s defined by matrices in a white background are not associative and hence they do not make A semigroups.
The two-element semigroup ({0,1}, 
)
The Cayley tableCayley table
A Cayley table, after the 19th century British mathematician Arthur Cayley, describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table...
for the semigroup ({0,1},
) is given below:  |
0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
This is the simplest non-trivial example of a semigroup that is not a group. This semigroup is commutative and has an identity element, which is 1 . It is not a group because the element 0 does not have an inverse. In fact, it is not even a cancellative semigroup because we cannot cancel the 0 in the equation 1·0 = 0·0.
This semigroup arises in various contexts. For instance, if we choose 1 to be the truth value "true
True
True may refer to:* Truth, the state of being in accord with fact or reality-Music:* True , 1996* True , 2002* True , 1983** "True"...
" and 0 to be the truth value "false
False
False or falsehood may refer to:*False *Lie or falsehood, a type of deception in the form of an untruthful statement*Falsity or falsehood, in law, deceitfulness by one party that results in damage to another...
" and the operation to be the logical connective
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
"and
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
", we obtain this semigroup in logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
. It is also isomorphic to the semigroup
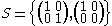
under matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
.
The two-element semigroup (Z2,+2)
The Cayley tableCayley table
A Cayley table, after the 19th century British mathematician Arthur Cayley, describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table...
for the semigroup (Z2,+2) is given below:
| +2 | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
This group is isomorphic to the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S2.
Finite semigroups of higher orders
Let A be the three-element set { 1, 2, 3 }. Altogether, a total of 39 = 19683 different binary operations can be defined on A. It is impractical to prepare a list of all these binary operations, and determine those that make A nonisomorphic semigroups.Algorithms and computer programs have been developed for determining nonisomorphic finite semigroups of a given order. These have been applied to determine the nonisomorphic semigroups of order three or higher. In fact, 113 of the 19683 binary operations determine 24 nonisomorphic semigroups, or 18 non-equivalent semigroups (with equivalence being isomorphism or anti-isomorphism). The number of nonisomorphic semigroups with n elements, for n a nonnegative integer, is listed under A027851 in the On-Line Encyclopedia of Integer Sequences. A001423 lists the number of non-equivalent semigroups, and A023814 the number of associative binary operations, out of a total of nn2, determining a semigroup.
See also
- Empty semigroupEmpty semigroupIn mathematics, a semigroup with no elements is a semigroup in which the underlying set is the empty set. Many authors do not admit the existence of such a semigroup. For them a semigroup is by definition a non-empty set together with an associative binary operation. However not all authors insist...
- Trivial semigroupTrivial semigroupIn mathematics, a trivial semigroup is a semigroup for which the cardinality of the underlying set is one. The number of distinct nonisomorphic semigroups with one element is one...
(Semigroup with one element) - Special classes of semigroupsSpecial classes of semigroupsIn mathematics, a semigroup is a nonempty set together with an associative binary operation. A special class of semigroups is a class of semigroups satisfying additional properties or conditions...