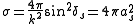Scattering length
Encyclopedia
The scattering length in quantum mechanics
describes low-energy scattering
. It is defined as the following low-energy limit
,
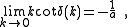
where is the scattering length,
is the scattering length, 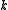 is the wave number, and
is the wave number, and  is the s-wave phase shift. The elastic cross section
is the s-wave phase shift. The elastic cross section
,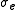 , at low energies is determined solely by the scattering length,
, at low energies is determined solely by the scattering length,
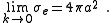
 one scatters off, but only how the potential looks at long length scales. The formal way to solve this problem is to do a partial wave expansion (somewhat analogous to the multipole expansion
one scatters off, but only how the potential looks at long length scales. The formal way to solve this problem is to do a partial wave expansion (somewhat analogous to the multipole expansion
in classical electrodynamics
), where one expands in the angular momentum
components of the outgoing wave. At very low energy the incoming particle does not see any structure, therefore to lowest order one has only a spherical symmetric outgoing wave, the so called s-wave scattering (angular momentum ). At higher energies one also needs to consider p and d-wave (
). At higher energies one also needs to consider p and d-wave (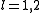 ) scattering and so on. The concept behind describing low energy properties in terms of a few parameters and symmetries is the idea of renormalization
) scattering and so on. The concept behind describing low energy properties in terms of a few parameters and symmetries is the idea of renormalization
.
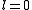 ) scattering length for a given potential we look at the infinitely repulsive spherical potential well
) scattering length for a given potential we look at the infinitely repulsive spherical potential well
of radius in 3 dimensions. The radial Schrödinger equation (
in 3 dimensions. The radial Schrödinger equation ( ) outside of the well is just the same as for a free particle:
) outside of the well is just the same as for a free particle:
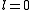
where the hard core potential requires that the wave function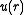 vanishes at
vanishes at 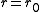 ,
,  .
.
The solution is readily found:
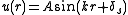 .
.
Here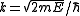 ;
;  is the s-wave phase shift (the phase difference between incoming and outgoing wave), which is fixed by the boundary condition
is the s-wave phase shift (the phase difference between incoming and outgoing wave), which is fixed by the boundary condition 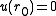 ;
; 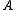 is an arbitrary normalization constant.
is an arbitrary normalization constant.
One can show that in general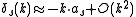 for small
for small 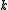 (i.e. low energy scattering). The parameter
(i.e. low energy scattering). The parameter  of dimension length is defined as the scattering length. For our potential we have therefore
of dimension length is defined as the scattering length. For our potential we have therefore 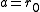 , in other words the scattering length for a hard sphere is just the radius. (Alternatively one could say that an arbitrary potential with s-wave scattering length
, in other words the scattering length for a hard sphere is just the radius. (Alternatively one could say that an arbitrary potential with s-wave scattering length 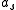 has the same low energy scattering properties as a hard sphere of radius
has the same low energy scattering properties as a hard sphere of radius 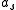 ).
).
To relate the scattering length to physical observables that can be measured in a scattering experiment we need to compute the cross section
 . In scattering theory
. In scattering theory
one writes the asymptotic wavefunction as (we assume there is a finite ranged scatterer at the origin and there is an incoming plane wave along the -axis)
-axis)
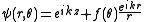
where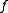 is the scattering amplitude
is the scattering amplitude
. According to the probability interpretation of quantum mechanics the differential cross section is given by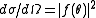 (the probability per unit time to scatter into the direction
(the probability per unit time to scatter into the direction 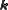 ). If we consider only s-wave scattering the differential cross section does not depend on the angle
). If we consider only s-wave scattering the differential cross section does not depend on the angle 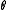 , and the total scattering cross section is just
, and the total scattering cross section is just 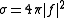 . The s-wave part of the wavefunction
. The s-wave part of the wavefunction 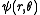 is projected out by using the standard expansion of a plane wave in terms of spherical waves and Legendre polynomials
is projected out by using the standard expansion of a plane wave in terms of spherical waves and Legendre polynomials 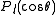
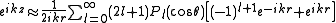
By matching the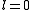 component of
component of 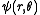 to the s-wave solution
to the s-wave solution 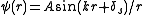 (where we normalize
(where we normalize 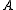 such that the incoming wave
such that the incoming wave 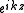 has a prefactor of unity) one has
has a prefactor of unity) one has
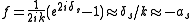
This gives
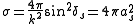
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
describes low-energy scattering
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
. It is defined as the following low-energy limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
,
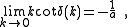
where
 is the scattering length,
is the scattering length, 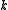 is the wave number, and
is the wave number, and  is the s-wave phase shift. The elastic cross section
is the s-wave phase shift. The elastic cross sectionCross section (physics)
A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....
,
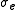 , at low energies is determined solely by the scattering length,
, at low energies is determined solely by the scattering length,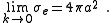
General concept
When a slow particle scatters off a short ranged scatterer (e.g. an impurity in a solid or a heavy particle) it cannot resolve the structure of the object since its de Broglie wavelength is very long. The idea is that then it should not be important what precise potentialScalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
 one scatters off, but only how the potential looks at long length scales. The formal way to solve this problem is to do a partial wave expansion (somewhat analogous to the multipole expansion
one scatters off, but only how the potential looks at long length scales. The formal way to solve this problem is to do a partial wave expansion (somewhat analogous to the multipole expansionMultipole expansion
A multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
in classical electrodynamics
Classical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
), where one expands in the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
components of the outgoing wave. At very low energy the incoming particle does not see any structure, therefore to lowest order one has only a spherical symmetric outgoing wave, the so called s-wave scattering (angular momentum
 ). At higher energies one also needs to consider p and d-wave (
). At higher energies one also needs to consider p and d-wave (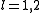 ) scattering and so on. The concept behind describing low energy properties in terms of a few parameters and symmetries is the idea of renormalization
) scattering and so on. The concept behind describing low energy properties in terms of a few parameters and symmetries is the idea of renormalizationRenormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
.
Example
As an example on how to compute the s-wave (i.e. angular momentum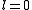 ) scattering length for a given potential we look at the infinitely repulsive spherical potential well
) scattering length for a given potential we look at the infinitely repulsive spherical potential wellPotential well
A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy because it is captured in the local minimum of a potential well...
of radius
 in 3 dimensions. The radial Schrödinger equation (
in 3 dimensions. The radial Schrödinger equation ( ) outside of the well is just the same as for a free particle:
) outside of the well is just the same as for a free particle: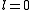
where the hard core potential requires that the wave function
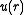 vanishes at
vanishes at 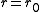 ,
,  .
.The solution is readily found:
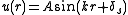 .
.Here
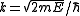 ;
;  is the s-wave phase shift (the phase difference between incoming and outgoing wave), which is fixed by the boundary condition
is the s-wave phase shift (the phase difference between incoming and outgoing wave), which is fixed by the boundary condition 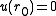 ;
; 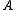 is an arbitrary normalization constant.
is an arbitrary normalization constant.One can show that in general
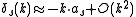 for small
for small 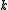 (i.e. low energy scattering). The parameter
(i.e. low energy scattering). The parameter  of dimension length is defined as the scattering length. For our potential we have therefore
of dimension length is defined as the scattering length. For our potential we have therefore 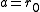 , in other words the scattering length for a hard sphere is just the radius. (Alternatively one could say that an arbitrary potential with s-wave scattering length
, in other words the scattering length for a hard sphere is just the radius. (Alternatively one could say that an arbitrary potential with s-wave scattering length 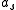 has the same low energy scattering properties as a hard sphere of radius
has the same low energy scattering properties as a hard sphere of radius 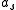 ).
).To relate the scattering length to physical observables that can be measured in a scattering experiment we need to compute the cross section
Cross section (physics)
A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....
 . In scattering theory
. In scattering theoryScattering theory
In mathematics and physics, scattering theory is a framework for studying and understanding the scattering of waves and particles. Prosaically, wave scattering corresponds to the collision and scattering of a wave with some material object, for instance sunlight scattered by rain drops to form a...
one writes the asymptotic wavefunction as (we assume there is a finite ranged scatterer at the origin and there is an incoming plane wave along the
 -axis)
-axis)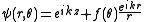
where
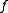 is the scattering amplitude
is the scattering amplitudeScattering amplitude
In quantum physics, the scattering amplitude is the amplitude of the outgoing spherical wave relative to the incoming plane wave in the stationary-state scattering process...
. According to the probability interpretation of quantum mechanics the differential cross section is given by
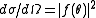 (the probability per unit time to scatter into the direction
(the probability per unit time to scatter into the direction 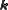 ). If we consider only s-wave scattering the differential cross section does not depend on the angle
). If we consider only s-wave scattering the differential cross section does not depend on the angle 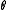 , and the total scattering cross section is just
, and the total scattering cross section is just 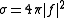 . The s-wave part of the wavefunction
. The s-wave part of the wavefunction 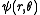 is projected out by using the standard expansion of a plane wave in terms of spherical waves and Legendre polynomials
is projected out by using the standard expansion of a plane wave in terms of spherical waves and Legendre polynomials 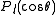
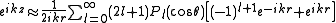
By matching the
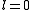 component of
component of 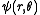 to the s-wave solution
to the s-wave solution 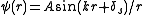 (where we normalize
(where we normalize 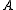 such that the incoming wave
such that the incoming wave 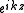 has a prefactor of unity) one has
has a prefactor of unity) one has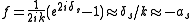
This gives