
Rubik's Cube
Encyclopedia
Rubik's Cube is a 3-D
mechanical puzzle
invented in 1974 by Hungarian sculptor and professor
of architecture
Ernő Rubik
.
Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp.
in 1980 and won the German Game of the Year
special award for Best Puzzle that year. As of January 2009, 350 million cubes had been sold worldwide making it the world's top-selling puzzle game. It is widely considered to be the world's best-selling toy.
In a classic Rubik's Cube, each of the six faces is covered by nine stickers, each of one of six solid colours, (traditionally white
, red
, blue
, orange, green
, and yellow
). A pivot mechanism enables each face to turn independently, thus mixing up the colours. For the puzzle to be solved, each face must be returned to consisting of one colour.
Similar puzzles have now been produced with various numbers of stickers, not all of them by Rubik.
On April 9, 1970, Frank Fox applied to patent his "Spherical 3×3×3". He received his UK patent (1344259) on January 16, 1974.
 In the mid-1970s, Ernő Rubik worked at the Department of Interior Design at the Academy of Applied Arts and Crafts
In the mid-1970s, Ernő Rubik worked at the Department of Interior Design at the Academy of Applied Arts and Crafts
in Budapest. Although it is widely reported that the Cube was built as a teaching tool to help his students understand 3D objects, his actual purpose was solving the structural problem of moving the parts independently without the entire mechanism falling apart. He did not realize that he had created a puzzle until the first time he scrambled his new Cube and then tried to restore it. Rubik obtained Hungarian patent HU170062 for his "Magic Cube" in 1975.
Rubik's Cube was first called the Magic Cube (Bűvös kocka) in Hungary. The puzzle had not been patented internationally within a year of the original patent. Patent law then prevented the possibility of an international patent. Ideal wanted at least a recognizable name to trademark; of course, that arrangement put Rubik in the spotlight because the Magic Cube was renamed after its inventor.
The first test batches of the product were produced in late 1977 and released to Budapest
toy shops. Magic Cube was held together with interlocking plastic pieces that prevented the puzzle being easily pulled apart, unlike the magnets in Nichols's design. In September 1979, a deal was signed with Ideal to release the Magic Cube world wide, and the puzzle made its international debut at the toy fairs of London, Paris, Nuremberg
and New York in January and February 1980.
After its international debut, the progress of the Cube towards the toy shop shelves of the West was briefly halted so that it could be manufactured to Western
safety and packaging specifications. A lighter Cube was produced, and Ideal decided to rename it. "The Gordian Knot
" and "Inca Gold" were considered, but the company finally decided on "Rubik's Cube", and the first batch was exported from Hungary in May 1980. Taking advantage of an initial shortage of Cubes, many imitations appeared.
to his employer Moleculon Research Corp., which sued Ideal in 1982. In 1984, Ideal lost the patent infringement suit and appealed. In 1986, the appeals court affirmed the judgment that Rubik's 2×2×2 Pocket Cube infringed Nichols's patent, but overturned the judgment on Rubik's 3×3×3 Cube.
Even while Rubik's patent application was being processed, Terutoshi Ishigi, a self-taught engineer and ironworks owner near Tokyo, filed for a Japanese patent for a nearly identical mechanism, which was granted in 1976 (Japanese patent publication JP55-008192). Until 1999, when an amended Japanese patent law
was enforced, Japan's patent office granted Japanese patents for non-disclosed technology within Japan without requiring worldwide novelty
. Hence, Ishigi's patent is generally accepted as an independent reinvention at that time.
Rubik applied for another Hungarian patent on October 28, 1980, and applied for other patents. In the United States, Rubik was granted on March 29, 1983, for the Cube.
Greek inventor Panagiotis Verdes patented a method of creating cubes beyond the 5×5×5, up to 11×11×11, in 2003 although he claims he originally thought of the idea around 1985. As of June 19, 2008, the 5×5×5
, 6×6×6
, and 7×7×7
models are in production in his "V-Cube" line.
 A standard Rubik's cube measures 5.7 cm (approximately 2¼ inches) on each side. The puzzle consists of twenty-six unique miniature cubes, also called "cubies" or "cubelets". Each of these includes a concealed inward extension that interlocks with the other cubes, while permitting them to move to different locations. However, the centre cube of each of the six faces is merely a single square façade; all six are affixed to the core mechanism. These provide structure for the other pieces to fit into and rotate around. So there are twenty-one pieces: a single core piece consisting of three intersecting axes holding the six centre squares in place but letting them rotate, and twenty smaller plastic pieces which fit into it to form the assembled puzzle.
A standard Rubik's cube measures 5.7 cm (approximately 2¼ inches) on each side. The puzzle consists of twenty-six unique miniature cubes, also called "cubies" or "cubelets". Each of these includes a concealed inward extension that interlocks with the other cubes, while permitting them to move to different locations. However, the centre cube of each of the six faces is merely a single square façade; all six are affixed to the core mechanism. These provide structure for the other pieces to fit into and rotate around. So there are twenty-one pieces: a single core piece consisting of three intersecting axes holding the six centre squares in place but letting them rotate, and twenty smaller plastic pieces which fit into it to form the assembled puzzle.
Each of the six centre pieces pivots on a screw (fastener) held by the centre piece, a "3-D cross". A spring between each screw head and its corresponding piece tensions the piece inward, so that collectively, the whole assembly remains compact, but can still be easily manipulated. The screw can be tightened or loosened to change the "feel" of the Cube. Newer official Rubik's brand cubes have rivets instead of screws and cannot be adjusted.
The Cube can be taken apart without much difficulty, typically by rotating the top layer by 45° and then prying one of its edge cubes away from the other two layers. Consequently it is a simple process to "solve" a Cube by taking it apart and reassembling it in a solved state.
There are six central pieces which show one coloured face, twelve edge pieces which show two coloured faces, and eight corner pieces which show three coloured faces. Each piece shows a unique colour combination, but not all combinations are present (for example, if red and orange are on opposite sides of the solved Cube, there is no edge piece with both red and orange sides). The location of these cubes relative to one another can be altered by twisting an outer third of the Cube 90°, 180° or 270°, but the location of the coloured sides relative to one another in the completed state of the puzzle cannot be altered: it is fixed by the relative positions of the centre squares. However, Cubes with alternative colour arrangements also exist; for example, with the yellow face opposite the green, the blue face opposite the white, and red and orange remaining opposite each other.
Douglas Hofstadter
, in the July 1982 issue of Scientific American, pointed out that Cubes could be coloured in such a way as to emphasise the corners or edges, rather than the faces as the standard colouring does; but neither of these alternative colourings has ever become popular.
(40,320) ways to arrange the corner cubes. Seven can be oriented independently, and the orientation of the eighth depends on the preceding seven, giving 37 (2,187) possibilities. There are 12!/2 (239,500,800) ways to arrange the edges, since an odd permutation of the corners implies an odd permutation of the edges as well. Eleven edges can be flipped independently, with the flip of the twelfth depending on the preceding ones, giving 211 (2,048) possibilities.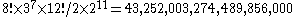
which is approximately forty-three quintillion.
The puzzle is often advertised as having only "billions
" of positions, as the larger numbers are unfamiliar to many. To put this into perspective, if one had as many 57-millimeter Rubik's Cubes as there are permutations, they could cover the Earth's surface 275 times.
The preceding figure is limited to permutations that can be reached solely by turning the sides of the cube. If one considers permutations reached through disassembly of the cube, the number becomes twelve times as large: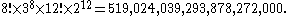
which is approximately five hundred and nineteen quintillion possible arrangements of the pieces that make up the Cube, but only one in twelve of these are actually solvable. This is because there is no sequence of moves that will swap a single pair of pieces or rotate a single corner or edge cube. Thus there are twelve possible sets of reachable configurations, sometimes called "universes" or "orbits", into which the Cube can be placed by dismantling and reassembling it.
magic square
or playing card
suits
. Thus one can nominally solve a Cube yet have the markings on the centres rotated; it then becomes an additional test to solve the centres as well.
Marking the Rubik's Cube increases its difficulty because this expands its set of distinguishable possible configurations. When the Cube is unscrambled apart from the orientations of the central squares, there will always be an even number of squares requiring a quarter turn. Thus there are 46/2 = 2,048 possible orientations of the centre squares in the otherwise unscrambled position, increasing the total number of possible Cube permutations from 43,252,003,274,489,856,000 (4.3×1019) to 88,580,102,706,155,225,088,000 (8.9×1022).
When turning a cube over is considered to be a change in permutation then we must also count arrangements of the centre faces. Nominally there are 6! ways to arrange the six centre faces of the cube, but only 24 of these are achievable without disassembly of the cube. When the orientations of centres are also counted, as above, this increases the total number of possible Cube permutations from 88,580,102,706,155,225,088,000 (8.9×1022) to 2,125,922,464,947,725,402,112,000 (2.1×1024).
, meaning a list of well-defined instructions for performing a task from a given initial state, through well-defined successive states, to a desired end-state. Each method of solving the Rubik's Cube employs its own set of algorithms, together with descriptions of what the effect of the algorithm is, and when it can be used to bring the cube closer to being solved.
Most algorithms are designed to transform only a small part of the cube without scrambling other parts that have already been solved, so that they can be applied repeatedly to different parts of the cube until the whole is solved. For example, there are well-known algorithms for cycling three corners without changing the rest of the puzzle, or flipping the orientation of a pair of edges while leaving the others intact.
Some algorithms have a certain desired effect on the cube (for example, swapping two corners) but may also have the side-effect of changing other parts of the cube (such as permuting some edges). Such algorithms are often simpler than the ones without side-effects, and are employed early on in the solution when most of the puzzle has not yet been solved and the side-effects are not important. Towards the end of the solution, the more specific (and usually more complicated) algorithms are used instead, to prevent scrambling parts of the puzzle that have already been solved.
to denote a sequence of moves, referred to as "Singmaster notation". Its relative nature allows algorithms to be written in such a way that they can be applied regardless of which side is designated the top or how the colours are organised on a particular cube.
When a prime symbol
( ′ ) follows a letter, it denotes a face turn counter-clockwise, while a letter without a prime symbol denotes a clockwise turn. A letter followed by a 2 (occasionally a superscript 2) denotes two turns, or a 180-degree turn. R is right side clockwise, but R is right side counter-clockwise. The letters x, y, and z are used to indicate that the entire Cube should be turned about one of its axes. When x, y or z are primed, it is an indication that the cube must be rotated in the opposite direction. When they are squared, the cube must be rotated twice.
For methods using middle-layer turns (particularly corners-first methods) there is a generally accepted "MES" extension to the notation where letters M, E, and S denote middle layer turns. It was used e.g. in Marc Waterman's Algorithm.
The 4×4×4 and larger cubes use an extended notation to refer to the additional middle layers. Generally speaking, uppercase letters (F B U D L R) refer to the outermost portions of the cube (called faces). Lowercase letters (ƒ b u d ℓ r) refer to the inner portions of the cube (called slices). An asterisk (L*), a number in front of it (2L), or two layers in parenthesis (Lℓ), means to turn the two layers at the same time (both the inner and the outer left faces) For example: (Rr)' ℓ2 ƒ' means to turn the two rightmost layers counterclockwise, then the left inner layer twice, and then the inner front layer counterclockwise.
Many general solutions for the Rubik's Cube have been discovered independently. The most popular method was developed by David Singmaster
and published in the book Notes on Rubik's "Magic Cube" in 1981. This solution involves solving the Cube layer by layer, in which one layer (designated the top) is solved first, followed by the middle layer, and then the final and bottom layer. After practice, solving the Cube layer by layer can be done in under one minute. Other general solutions include "corners first" methods or combinations of several other methods. In 1982, David Singmaster and Alexander Frey hypothesised that the number of moves needed to solve the Rubik's Cube, given an ideal algorithm, might be in "the low twenties". In 2007, Daniel Kunkle and Gene Cooperman used computer search methods to demonstrate that any 3×3×3 Rubik's Cube configuration can be solved in 26 moves or fewer.
In 2008, Tomas Rokicki lowered that number to 22 moves, and in July 2010, a team of researchers including Rokicki, working with Google
, proved the so-called "God's number
" to be 20. This is optimal, since there exist some starting positions which require at least 20 moves to solve. More generally, it has been shown that an n × n × n Rubik's Cube can be solved optimally in Θ(n2 / log(n))
moves.
A solution commonly used by speed cubers was developed by Jessica Fridrich
. It is similar to the layer-by-layer method but employs the use of a large number of algorithms, especially for orienting and permuting the last layer. The cross is done first followed by first-layer corners and second layer edges simultaneously, with each corner paired up with a second-layer edge piece, thus completing the first two layers (F2L). This is then followed by orienting
the last layer then permuting
the last layer (OLL and PLL respectively). Fridrich's solution
requires learning roughly 120 algorithms but allows the Cube to be solved in only 55 moves on average.
Philip Marshall's The Ultimate Solution to Rubik's Cube is a modified version of Fridrich's method, averaging only 65 twists yet requiring the memorization of only two algorithms.
A now well-known method was developed by Lars Petrus
. In this method, a 2×2×2 section is solved first, followed by a 2×2×3, and then the incorrect edges are solved using a three-move algorithm, which eliminates the need for a possible 32-move algorithm later. The principle behind this is that in layer by layer you must constantly break and fix the first layer; the 2×2×2 and 2×2×3 sections allow three or two layers to be turned without ruining progress. One of the advantages of this method is that it tends to give solutions in fewer moves.
In 1997, Denny Dedmore published a solution described using diagrammatic icons representing the moves to be made, instead of the usual notation.
(or speedsolving) is the practice of trying to solve a Rubik's Cube in the shortest time possible. There are a number of speedcubing competitions that take place around the world.
The first world championship organised by the Guinness Book of World Records was held in Munich
on March 13, 1981. All Cubes were moved 40 times and lubricated with petroleum jelly
. The official winner, with a record of 38 seconds, was Jury Froeschl, born in Munich
. The first international world championship was held in Budapest
on June 5, 1982, and was won by Minh Thai
, a Vietnamese student from Los Angeles
, with a time of 22.95 seconds.
Since 2003, the winner of a competition is determined by taking the average time of the middle three of five attempts. However, the single best time of all tries is also recorded.
The World Cube Association
maintains a history of world records.
In 2004, the WCA made it mandatory to use a special timing device called a Stackmat timer
.
In addition to official competitions, informal alternative competitions have been held which invite participants to solve the Cube in unusual situations. Some such situations include:
Of these informal competitions, the World Cube Association sanctions only blindfolded, one-handed, and feet solving as official competition events.
In blindfolded solving, the contestant first studies the scrambled cube (i.e., looking at it normally with no blindfold), and is then blindfolded before beginning to turn the cube's faces. Their recorded time for this event includes both the time spent examining the cube and the time spent manipulating it.
, who had a best time of 5.66 seconds at the Melbourne Winter Open 2011. The world record for average time per solve is also currently held by Zemdegs. At the same competition, he set a 7.64 second average .
On March 17, 2010, 134 school boys from Dr Challoner's Grammar School, Amersham, England broke the previous Guinness World Record for most people solving a Rubik's cube at once in 12 minutes. The previous record set in December 2008 in Santa Ana, CA achieved 96 completions.
Image:Rubik's Cube variants.jpg|thumb|250px|alt=Rubik's Cube Variants|Variations of Rubik's Cubes, clockwise from upper left: V-Cube 7
, Professor's Cube
, V-Cube 6
, Pocket Cube
, original Rubik's Cube, Rubik's Revenge
. Clicking on a cube in the picture will redirect to the respective cube's page.
default none
poly 964 370 1082 448 1065 545 970 622 865 545 875 445 Pocket Cube
poly 620 370 844 363 862 536 850 680 628 682 Rubik's Cube
poly 455 280 570 440 580 605 355 705 255 530 220 363 Rubik's Revenge
poly 540 75 780 90 780 225 760 360 620 365 605 420 560 420 505 340 500 235 Professor's Cube
poly 890 50 1125 90 1065 420 1040 420 965 365 930 390 850 380 845 365 830 360 840 205 V-Cube 6
poly 255 50 320 90 405 225 420 290 210 360 230 460 210 465 150 410 90 320 60 240 45 155 120 100 190 70 V-Cube 7
There are different variations of Rubik's Cubes with up to seven layers: the 2×2×2 (Pocket/Mini Cube
), the standard 3×3×3 cube, the 4×4×4 (Rubik's Revenge/Master Cube
), and the 5×5×5 (Professor's Cube
), the 6×6×6 (V-Cube 6
), and 7×7×7 (V-Cube 7
).
CESailor Tech's E-cube is an electronic variant of the 3×3×3 cube, made with RGB LEDs and switches. There are two switches on each row and column. Pressing the switches indicates the direction of rotation, which causes the LED display to change colours, simulating real rotations. The product was demonstrated at the Taiwan government show of college designs on October 30, 2008.
Another electronic variation of the 3×3×3 Cube is the Rubik's TouchCube. Sliding a finger across its faces causes its patterns of coloured lights to rotate the same way they would on a mechanical cube. The TouchCube was introduced at the American International Toy Fair
in New York on February 15, 2009.
The Cube has inspired an entire category of similar puzzles, commonly referred to as twisty puzzles
, which includes the cubes of different sizes mentioned above as well as various other geometric shapes. Some such shapes include the tetrahedron
(Pyraminx
), the octahedron
(Skewb Diamond
), the dodecahedron (Megaminx
), the icosahedron
(Dogic
). There are also puzzles that change shape such as Rubik's Snake
and the Square One
.
Some custom puzzles are not derived from any existing mechanism, such as the Gigaminx v1.5-v2, Bevel Cube, SuperX, Toru, Rua, and 1×2×3. These puzzles usually have a set of masters 3D printed, which then are copied using molding and casting techniques to create the final puzzle.
Other Rubik's Cube modifications include cubes that have been extended or truncated to form a new shape. An example of this is the Trabjer's Octahedron, which can be built by truncating and extending portions of a regular 3×3. Most shape mods can be adapted to higher-order cubes. In the case of Tony Fisher's Rhombic Dodecahedron, there are 3×3, 4×4, 5×5, and 6×6 versions of the puzzle.

 Puzzles like the Rubik's Cube can be simulated by computer software, which provide functions such as recording of player metrics, storing scrambled Cube positions, conducting online competitions, analyzing of move sequences, and converting between different move notations. Software can also simulate very large puzzles that are impractical to build, such as 100×100×100 and 1,000×1,000×1,000 cubes, as well as virtual puzzles that cannot be physically built, such as 4- and 5-dimensional analogues of the cube.
Puzzles like the Rubik's Cube can be simulated by computer software, which provide functions such as recording of player metrics, storing scrambled Cube positions, conducting online competitions, analyzing of move sequences, and converting between different move notations. Software can also simulate very large puzzles that are impractical to build, such as 100×100×100 and 1,000×1,000×1,000 cubes, as well as virtual puzzles that cannot be physically built, such as 4- and 5-dimensional analogues of the cube.
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
mechanical puzzle
Mechanical puzzle
A mechanical puzzle is a puzzle presented as a set of mechanically interlinked pieces.- History :The oldest known mechanical puzzle comes from Greece and appeared in the 3rd century BC....
invented in 1974 by Hungarian sculptor and professor
Professor
A professor is a scholarly teacher; the precise meaning of the term varies by country. Literally, professor derives from Latin as a "person who professes" being usually an expert in arts or sciences; a teacher of high rank...
of architecture
Architecture
Architecture is both the process and product of planning, designing and construction. Architectural works, in the material form of buildings, are often perceived as cultural and political symbols and as works of art...
Ernő Rubik
Erno Rubik
Ernő Rubik is a Hungarian inventor, architect and professor of architecture. He is best known for the invention of mechanical puzzles including Rubik's Cube , Rubik's Magic, Rubik's Magic: Master Edition, Rubik's Snake and Rubik's 360....
.
Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp.
Ideal Toy Company
Ideal Toy Company was founded as Ideal Novelty and Toy Company in New York in 1907 by Morris and Rose Michtom after they had invented the Teddy bear in 1903. The company changed its name to Ideal Toy Company in 1938...
in 1980 and won the German Game of the Year
Spiel des Jahres
The Spiel des Jahres is an award for board and card games, created in 1978 with the stated purpose of rewarding excellence in game design, and promoting top-quality games in the German market. It is thought that the existence and popularity of the award is one of the major drivers of the quality...
special award for Best Puzzle that year. As of January 2009, 350 million cubes had been sold worldwide making it the world's top-selling puzzle game. It is widely considered to be the world's best-selling toy.
In a classic Rubik's Cube, each of the six faces is covered by nine stickers, each of one of six solid colours, (traditionally white
White
White is a color, the perception of which is evoked by light that stimulates all three types of color sensitive cone cells in the human eye in nearly equal amounts and with high brightness compared to the surroundings. A white visual stimulation will be void of hue and grayness.White light can be...
, red
Red
Red is any of a number of similar colors evoked by light consisting predominantly of the longest wavelengths of light discernible by the human eye, in the wavelength range of roughly 630–740 nm. Longer wavelengths than this are called infrared , and cannot be seen by the naked eye...
, blue
Blue
Blue is a colour, the perception of which is evoked by light having a spectrum dominated by energy with a wavelength of roughly 440–490 nm. It is considered one of the additive primary colours. On the HSV Colour Wheel, the complement of blue is yellow; that is, a colour corresponding to an equal...
, orange, green
Green
Green is a color, the perception of which is evoked by light having a spectrum dominated by energy with a wavelength of roughly 520–570 nanometres. In the subtractive color system, it is not a primary color, but is created out of a mixture of yellow and blue, or yellow and cyan; it is considered...
, and yellow
Yellow
Yellow is the color evoked by light that stimulates both the L and M cone cells of the retina about equally, with no significant stimulation of the S cone cells. Light with a wavelength of 570–590 nm is yellow, as is light with a suitable mixture of red and green...
). A pivot mechanism enables each face to turn independently, thus mixing up the colours. For the puzzle to be solved, each face must be returned to consisting of one colour.
Similar puzzles have now been produced with various numbers of stickers, not all of them by Rubik.
Prior attempts
In March 1970, Larry Nichols invented a 2×2×2 "Puzzle with Pieces Rotatable in Groups" and filed a Canadian patent application for it. Nichols's cube was held together with magnets. Nichols was granted on April 11, 1972, two years before Rubik invented his Cube.On April 9, 1970, Frank Fox applied to patent his "Spherical 3×3×3". He received his UK patent (1344259) on January 16, 1974.
Rubik's invention

Moholy-Nagy University of Art and Design
The Moholy-Nagy University of Art and Design , former Hungarian University of Arts and Design, is located in Budapest, Hungary. The university is committed to training traditional artist-craftsmen, as well as architects, designers and visual communication designers...
in Budapest. Although it is widely reported that the Cube was built as a teaching tool to help his students understand 3D objects, his actual purpose was solving the structural problem of moving the parts independently without the entire mechanism falling apart. He did not realize that he had created a puzzle until the first time he scrambled his new Cube and then tried to restore it. Rubik obtained Hungarian patent HU170062 for his "Magic Cube" in 1975.
Rubik's Cube was first called the Magic Cube (Bűvös kocka) in Hungary. The puzzle had not been patented internationally within a year of the original patent. Patent law then prevented the possibility of an international patent. Ideal wanted at least a recognizable name to trademark; of course, that arrangement put Rubik in the spotlight because the Magic Cube was renamed after its inventor.
The first test batches of the product were produced in late 1977 and released to Budapest
Budapest
Budapest is the capital of Hungary. As the largest city of Hungary, it is the country's principal political, cultural, commercial, industrial, and transportation centre. In 2011, Budapest had 1,733,685 inhabitants, down from its 1989 peak of 2,113,645 due to suburbanization. The Budapest Commuter...
toy shops. Magic Cube was held together with interlocking plastic pieces that prevented the puzzle being easily pulled apart, unlike the magnets in Nichols's design. In September 1979, a deal was signed with Ideal to release the Magic Cube world wide, and the puzzle made its international debut at the toy fairs of London, Paris, Nuremberg
Nuremberg International Toy Fair
Spielwarenmesse International Toy Fair Nürnberg is the largest international trade fair for toys and games. Only trade visitors associated with the toy business, journalists and invited guests are admitted...
and New York in January and February 1980.
After its international debut, the progress of the Cube towards the toy shop shelves of the West was briefly halted so that it could be manufactured to Western
Western world
The Western world, also known as the West and the Occident , is a term referring to the countries of Western Europe , the countries of the Americas, as well all countries of Northern and Central Europe, Australia and New Zealand...
safety and packaging specifications. A lighter Cube was produced, and Ideal decided to rename it. "The Gordian Knot
Gordian Knot
The Gordian Knot is a legend of Phrygian Gordium associated with Alexander the Great. It is often used as a metaphor for an intractable problem solved by a bold stroke :"Turn him to any cause of policy,...
" and "Inca Gold" were considered, but the company finally decided on "Rubik's Cube", and the first batch was exported from Hungary in May 1980. Taking advantage of an initial shortage of Cubes, many imitations appeared.
Patent disputes
Nichols assigned his patentPatent
A patent is a form of intellectual property. It consists of a set of exclusive rights granted by a sovereign state to an inventor or their assignee for a limited period of time in exchange for the public disclosure of an invention....
to his employer Moleculon Research Corp., which sued Ideal in 1982. In 1984, Ideal lost the patent infringement suit and appealed. In 1986, the appeals court affirmed the judgment that Rubik's 2×2×2 Pocket Cube infringed Nichols's patent, but overturned the judgment on Rubik's 3×3×3 Cube.
Even while Rubik's patent application was being processed, Terutoshi Ishigi, a self-taught engineer and ironworks owner near Tokyo, filed for a Japanese patent for a nearly identical mechanism, which was granted in 1976 (Japanese patent publication JP55-008192). Until 1999, when an amended Japanese patent law
Japanese patent law
Japanese patent law is based on the first-to-file principle and is mainly given force by the Patent Act of Japan. Article 2 defines an invention as "the highly advanced creation of technical ideas by which a law of nature is utilized"...
was enforced, Japan's patent office granted Japanese patents for non-disclosed technology within Japan without requiring worldwide novelty
Novelty (patent)
Novelty is a patentability requirement. An invention is not patentable if the claimed subject matter was disclosed before the date of filing, or before the date of priority if a priority is claimed, of the patent application....
. Hence, Ishigi's patent is generally accepted as an independent reinvention at that time.
Rubik applied for another Hungarian patent on October 28, 1980, and applied for other patents. In the United States, Rubik was granted on March 29, 1983, for the Cube.
Greek inventor Panagiotis Verdes patented a method of creating cubes beyond the 5×5×5, up to 11×11×11, in 2003 although he claims he originally thought of the idea around 1985. As of June 19, 2008, the 5×5×5
Professor's Cube
The Professor's Cube is a mechanical puzzle, a 5×5×5 version of the Rubik's Cube. It has qualities in common with both the original 3×3×3 Rubik's Cube and the 4×4×4 Rubik's Revenge, and knowing the solution to either can help when working on the 5×5×5 cube....
, 6×6×6
V-Cube 6
The V-Cube 6 is the 6×6×6 version of Rubik's Cube. Unlike the original puzzle , it has no fixed facets: the center facets are free to move to different positions...
, and 7×7×7
V-Cube 7
The V-Cube 7 is the 7×7×7 version of Rubik's Cube. It was invented by Panagiotis Verdes and is produced by his company, Verdes Innovations SA. Like the 5×5×5, the V-Cube 7 has both fixed and movable center facets.- Mechanics :...
models are in production in his "V-Cube" line.
Mechanics

Each of the six centre pieces pivots on a screw (fastener) held by the centre piece, a "3-D cross". A spring between each screw head and its corresponding piece tensions the piece inward, so that collectively, the whole assembly remains compact, but can still be easily manipulated. The screw can be tightened or loosened to change the "feel" of the Cube. Newer official Rubik's brand cubes have rivets instead of screws and cannot be adjusted.
The Cube can be taken apart without much difficulty, typically by rotating the top layer by 45° and then prying one of its edge cubes away from the other two layers. Consequently it is a simple process to "solve" a Cube by taking it apart and reassembling it in a solved state.
There are six central pieces which show one coloured face, twelve edge pieces which show two coloured faces, and eight corner pieces which show three coloured faces. Each piece shows a unique colour combination, but not all combinations are present (for example, if red and orange are on opposite sides of the solved Cube, there is no edge piece with both red and orange sides). The location of these cubes relative to one another can be altered by twisting an outer third of the Cube 90°, 180° or 270°, but the location of the coloured sides relative to one another in the completed state of the puzzle cannot be altered: it is fixed by the relative positions of the centre squares. However, Cubes with alternative colour arrangements also exist; for example, with the yellow face opposite the green, the blue face opposite the white, and red and orange remaining opposite each other.
Douglas Hofstadter
Douglas Hofstadter
Douglas Richard Hofstadter is an American academic whose research focuses on consciousness, analogy-making, artistic creation, literary translation, and discovery in mathematics and physics...
, in the July 1982 issue of Scientific American, pointed out that Cubes could be coloured in such a way as to emphasise the corners or edges, rather than the faces as the standard colouring does; but neither of these alternative colourings has ever become popular.
Permutations
The original (3×3×3) Rubik's Cube has eight corners and twelve edges. There are 8!Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
(40,320) ways to arrange the corner cubes. Seven can be oriented independently, and the orientation of the eighth depends on the preceding seven, giving 37 (2,187) possibilities. There are 12!/2 (239,500,800) ways to arrange the edges, since an odd permutation of the corners implies an odd permutation of the edges as well. Eleven edges can be flipped independently, with the flip of the twelfth depending on the preceding ones, giving 211 (2,048) possibilities.
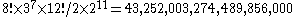
which is approximately forty-three quintillion.
The puzzle is often advertised as having only "billions
1000000000 (number)
1,000,000,000 is the natural number following 999,999,999 and preceding 1,000,000,001.In scientific notation, it is written as 109....
" of positions, as the larger numbers are unfamiliar to many. To put this into perspective, if one had as many 57-millimeter Rubik's Cubes as there are permutations, they could cover the Earth's surface 275 times.
The preceding figure is limited to permutations that can be reached solely by turning the sides of the cube. If one considers permutations reached through disassembly of the cube, the number becomes twelve times as large:
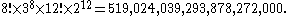
which is approximately five hundred and nineteen quintillion possible arrangements of the pieces that make up the Cube, but only one in twelve of these are actually solvable. This is because there is no sequence of moves that will swap a single pair of pieces or rotate a single corner or edge cube. Thus there are twelve possible sets of reachable configurations, sometimes called "universes" or "orbits", into which the Cube can be placed by dismantling and reassembling it.
Centre faces
The original Rubik's Cube had no orientation markings on the centre faces (although some carried the words "Rubik's Cube" on the centre square of the white face), and therefore solving it does not require any attention to orienting those faces correctly. However, with marker pens, one could, for example, mark the central squares of an unscrambled Cube with four coloured marks on each edge, each corresponding to the colour of the adjacent face. Some Cubes have also been produced commercially with markings on all of the squares, such as the Lo ShuLo Shu Square
Lo Shu Square |Luo ]] Book/Scroll) or the Nine Halls Diagram , is the unique normal magic square of order three. Lo Shu is part of the legacy of the most ancient Chinese mathematical and divinatory traditions, and is an important emblem in Feng Shui , the art of geomancy concerned with the...
magic square
Magic square
In recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n2...
or playing card
Playing card
A playing card is a piece of specially prepared heavy paper, thin cardboard, plastic-coated paper, cotton-paper blend, or thin plastic, marked with distinguishing motifs and used as one of a set for playing card games...
suits
Suit (cards)
In playing cards, a suit is one of several categories into which the cards of a deck are divided. Most often, each card bears one of several symbols showing to which suit it belongs; the suit may alternatively or in addition be indicated by the color printed on the card...
. Thus one can nominally solve a Cube yet have the markings on the centres rotated; it then becomes an additional test to solve the centres as well.
Marking the Rubik's Cube increases its difficulty because this expands its set of distinguishable possible configurations. When the Cube is unscrambled apart from the orientations of the central squares, there will always be an even number of squares requiring a quarter turn. Thus there are 46/2 = 2,048 possible orientations of the centre squares in the otherwise unscrambled position, increasing the total number of possible Cube permutations from 43,252,003,274,489,856,000 (4.3×1019) to 88,580,102,706,155,225,088,000 (8.9×1022).
When turning a cube over is considered to be a change in permutation then we must also count arrangements of the centre faces. Nominally there are 6! ways to arrange the six centre faces of the cube, but only 24 of these are achievable without disassembly of the cube. When the orientations of centres are also counted, as above, this increases the total number of possible Cube permutations from 88,580,102,706,155,225,088,000 (8.9×1022) to 2,125,922,464,947,725,402,112,000 (2.1×1024).
Algorithms
In Rubik's cubists' parlance, a memorised sequence of moves that has a desired effect on the cube is called an algorithm. This terminology is derived from the mathematical use of algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, meaning a list of well-defined instructions for performing a task from a given initial state, through well-defined successive states, to a desired end-state. Each method of solving the Rubik's Cube employs its own set of algorithms, together with descriptions of what the effect of the algorithm is, and when it can be used to bring the cube closer to being solved.
Most algorithms are designed to transform only a small part of the cube without scrambling other parts that have already been solved, so that they can be applied repeatedly to different parts of the cube until the whole is solved. For example, there are well-known algorithms for cycling three corners without changing the rest of the puzzle, or flipping the orientation of a pair of edges while leaving the others intact.
Some algorithms have a certain desired effect on the cube (for example, swapping two corners) but may also have the side-effect of changing other parts of the cube (such as permuting some edges). Such algorithms are often simpler than the ones without side-effects, and are employed early on in the solution when most of the puzzle has not yet been solved and the side-effects are not important. Towards the end of the solution, the more specific (and usually more complicated) algorithms are used instead, to prevent scrambling parts of the puzzle that have already been solved.
Move notation
Many 3×3×3 Rubik's Cube enthusiasts use a notation developed by David SingmasterDavid Singmaster
David Breyer Singmaster is a retired professor of mathematics at London South Bank University, England, UK. A self-described metagrobologist, he is most famous for his solution to the Rubik's cube and his huge personal collection of mechanical puzzles and books of brain teasers. He is also...
to denote a sequence of moves, referred to as "Singmaster notation". Its relative nature allows algorithms to be written in such a way that they can be applied regardless of which side is designated the top or how the colours are organised on a particular cube.
- F (Front): the side currently facing the solver
- B (Back): the side opposite the front
- U (Up): the side above or on top of the front side
- D (Down): the side opposite the top, underneath the Cube
- L (Left): the side directly to the left of the front
- R (Right): the side directly to the right of the front
- ƒ (Front two layers): the side facing the solver and the corresponding middle layer
- b (Back two layers): the side opposite the front and the corresponding middle layer
- u (Up two layers) : the top side and the corresponding middle layer
- d (Down two layers) : the bottom layer and the corresponding middle layer
- l (Left two layers) : the side to the left of the front and the corresponding middle layer
- r (Right two layers) : the side to the right of the front and the corresponding middle layer
- x (rotate): rotate the entire Cube on R
- y (rotate): rotate the entire Cube on U
- z (rotate): rotate the entire Cube on F
When a prime symbol
Prime (symbol)
The prime symbol , double prime symbol , and triple prime symbol , etc., are used to designate several different units, and for various other purposes in mathematics, the sciences and linguistics...
( ′ ) follows a letter, it denotes a face turn counter-clockwise, while a letter without a prime symbol denotes a clockwise turn. A letter followed by a 2 (occasionally a superscript 2) denotes two turns, or a 180-degree turn. R is right side clockwise, but R is right side counter-clockwise. The letters x, y, and z are used to indicate that the entire Cube should be turned about one of its axes. When x, y or z are primed, it is an indication that the cube must be rotated in the opposite direction. When they are squared, the cube must be rotated twice.
For methods using middle-layer turns (particularly corners-first methods) there is a generally accepted "MES" extension to the notation where letters M, E, and S denote middle layer turns. It was used e.g. in Marc Waterman's Algorithm.
- M (Middle): the layer between L and R, turn direction as L (top-down)
- E (Equator): the layer between U and D, turn direction as D (left-right)
- S (Standing): the layer between F and B, turn direction as F
The 4×4×4 and larger cubes use an extended notation to refer to the additional middle layers. Generally speaking, uppercase letters (F B U D L R) refer to the outermost portions of the cube (called faces). Lowercase letters (ƒ b u d ℓ r) refer to the inner portions of the cube (called slices). An asterisk (L*), a number in front of it (2L), or two layers in parenthesis (Lℓ), means to turn the two layers at the same time (both the inner and the outer left faces) For example: (Rr)
Optimal solutions
Although there are a significant number of possible permutations for the Rubik's Cube, a number of solutions have been developed which allow for the cube to be solved in well under 100 moves.Many general solutions for the Rubik's Cube have been discovered independently. The most popular method was developed by David Singmaster
David Singmaster
David Breyer Singmaster is a retired professor of mathematics at London South Bank University, England, UK. A self-described metagrobologist, he is most famous for his solution to the Rubik's cube and his huge personal collection of mechanical puzzles and books of brain teasers. He is also...
and published in the book Notes on Rubik's "Magic Cube" in 1981. This solution involves solving the Cube layer by layer, in which one layer (designated the top) is solved first, followed by the middle layer, and then the final and bottom layer. After practice, solving the Cube layer by layer can be done in under one minute. Other general solutions include "corners first" methods or combinations of several other methods. In 1982, David Singmaster and Alexander Frey hypothesised that the number of moves needed to solve the Rubik's Cube, given an ideal algorithm, might be in "the low twenties". In 2007, Daniel Kunkle and Gene Cooperman used computer search methods to demonstrate that any 3×3×3 Rubik's Cube configuration can be solved in 26 moves or fewer.
In 2008, Tomas Rokicki lowered that number to 22 moves, and in July 2010, a team of researchers including Rokicki, working with Google
Google
Google Inc. is an American multinational public corporation invested in Internet search, cloud computing, and advertising technologies. Google hosts and develops a number of Internet-based services and products, and generates profit primarily from advertising through its AdWords program...
, proved the so-called "God's number
God's algorithm
God's algorithm is a notion originating in discussions of ways to solve the Rubik's Cube puzzle, but which can also be applied to other combinatorial puzzles and mathematical games...
" to be 20. This is optimal, since there exist some starting positions which require at least 20 moves to solve. More generally, it has been shown that an n × n × n Rubik's Cube can be solved optimally in Θ(n2 / log(n))
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
moves.
A solution commonly used by speed cubers was developed by Jessica Fridrich
Jessica Fridrich
Jessica Fridrich is the inventor of the most commonly used method for speed-solving the Rubik's Cube, better known as speedcubing.This method describes solving the cube in a layer-by-layer fashion. First a so-called "cross" is made on the first layer, consisting of the center piece and four edges...
. It is similar to the layer-by-layer method but employs the use of a large number of algorithms, especially for orienting and permuting the last layer. The cross is done first followed by first-layer corners and second layer edges simultaneously, with each corner paired up with a second-layer edge piece, thus completing the first two layers (F2L). This is then followed by orienting
Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
the last layer then permuting
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
the last layer (OLL and PLL respectively). Fridrich's solution
Fridrich Method
The CFOP system, simply known as the Fridrich Method is one of the most commonly used methods in speedsolving a Rubik's Cube...
requires learning roughly 120 algorithms but allows the Cube to be solved in only 55 moves on average.
Philip Marshall's The Ultimate Solution to Rubik's Cube is a modified version of Fridrich's method, averaging only 65 twists yet requiring the memorization of only two algorithms.
A now well-known method was developed by Lars Petrus
Lars Petrus
Lars Petrus made his name as an internationally accomplished speedcuber in 1982 when he became the national champion of Sweden, and went on to finish fourth overall at the first official Rubik's Cube World Championships held in Budapest, Hungary. He later published his unique method, known as the...
. In this method, a 2×2×2 section is solved first, followed by a 2×2×3, and then the incorrect edges are solved using a three-move algorithm, which eliminates the need for a possible 32-move algorithm later. The principle behind this is that in layer by layer you must constantly break and fix the first layer; the 2×2×2 and 2×2×3 sections allow three or two layers to be turned without ruining progress. One of the advantages of this method is that it tends to give solutions in fewer moves.
In 1997, Denny Dedmore published a solution described using diagrammatic icons representing the moves to be made, instead of the usual notation.
Speedcubing competitions
SpeedcubingSpeedcubing
Speedcubing is the activity of solving a Rubik's Cube or related puzzle as quickly as possible...
(or speedsolving) is the practice of trying to solve a Rubik's Cube in the shortest time possible. There are a number of speedcubing competitions that take place around the world.
The first world championship organised by the Guinness Book of World Records was held in Munich
Munich
Munich The city's motto is "" . Before 2006, it was "Weltstadt mit Herz" . Its native name, , is derived from the Old High German Munichen, meaning "by the monks' place". The city's name derives from the monks of the Benedictine order who founded the city; hence the monk depicted on the city's coat...
on March 13, 1981. All Cubes were moved 40 times and lubricated with petroleum jelly
Petroleum jelly
Petroleum jelly, petrolatum, white petrolatum or soft paraffin, CAS number 8009-03-8, is a semi-solid mixture of hydrocarbons , originally promoted as a topical ointment for its healing properties...
. The official winner, with a record of 38 seconds, was Jury Froeschl, born in Munich
Munich
Munich The city's motto is "" . Before 2006, it was "Weltstadt mit Herz" . Its native name, , is derived from the Old High German Munichen, meaning "by the monks' place". The city's name derives from the monks of the Benedictine order who founded the city; hence the monk depicted on the city's coat...
. The first international world championship was held in Budapest
Budapest
Budapest is the capital of Hungary. As the largest city of Hungary, it is the country's principal political, cultural, commercial, industrial, and transportation centre. In 2011, Budapest had 1,733,685 inhabitants, down from its 1989 peak of 2,113,645 due to suburbanization. The Budapest Commuter...
on June 5, 1982, and was won by Minh Thai
Minh Thai
Minh Thai was a sixteen-year-old Vietnamese high school student from Los Angeles when he won the first world championship on June 5, 1982 in Budapest by solving a Rubik's Cube in 22.95 seconds....
, a Vietnamese student from Los Angeles
Los Angeles, California
Los Angeles , with a population at the 2010 United States Census of 3,792,621, is the most populous city in California, USA and the second most populous in the United States, after New York City. It has an area of , and is located in Southern California...
, with a time of 22.95 seconds.
Since 2003, the winner of a competition is determined by taking the average time of the middle three of five attempts. However, the single best time of all tries is also recorded.
The World Cube Association
World Cube Association
The World Cube Association is an organization that regulates and holds Rubik's Cube competitions. It was founded by Ron van Bruchem of the Netherlands and Tyson Mao of the United States...
maintains a history of world records.
In 2004, the WCA made it mandatory to use a special timing device called a Stackmat timer
Stackmat timer
StackMat timers are timing devices designed for use in sport stacking and speedcubing. StackMat timers have two touchpads, one on each side of the display. The hands are placed on the two touch pads. After about a second, a green light will light up, and when one or both of the hands are released...
.
In addition to official competitions, informal alternative competitions have been held which invite participants to solve the Cube in unusual situations. Some such situations include:
- Blindfolded solving
- Solving the Cube with one person blindfolded and the other person saying what moves to make, known as "Team Blindfold"
- Solving the Cube underwater in a single breath
- Solving the Cube using a single hand
- Solving the Cube with one's feet
Of these informal competitions, the World Cube Association sanctions only blindfolded, one-handed, and feet solving as official competition events.
In blindfolded solving, the contestant first studies the scrambled cube (i.e., looking at it normally with no blindfold), and is then blindfolded before beginning to turn the cube's faces. Their recorded time for this event includes both the time spent examining the cube and the time spent manipulating it.
Records
The current world record for single time on a 3×3×3 Rubik's Cube was set by Feliks ZemdegsFeliks Zemdegs
Feliks Zemdegs is an Australian Rubik's Cube speedsolver. The surname is Latvian.He bought his first cube in April 2008 inspired by speedcubing videos and tutorials on Youtube. The first unofficial time he recorded was an average of 19.73 seconds on 14 June 2008...
, who had a best time of 5.66 seconds at the Melbourne Winter Open 2011. The world record for average time per solve is also currently held by Zemdegs. At the same competition, he set a 7.64 second average .
On March 17, 2010, 134 school boys from Dr Challoner's Grammar School, Amersham, England broke the previous Guinness World Record for most people solving a Rubik's cube at once in 12 minutes. The previous record set in December 2008 in Santa Ana, CA achieved 96 completions.
Variations
Image:Rubik's Cube variants.jpg|thumb|250px|alt=Rubik's Cube Variants|Variations of Rubik's Cubes, clockwise from upper left: V-Cube 7
V-Cube 7
The V-Cube 7 is the 7×7×7 version of Rubik's Cube. It was invented by Panagiotis Verdes and is produced by his company, Verdes Innovations SA. Like the 5×5×5, the V-Cube 7 has both fixed and movable center facets.- Mechanics :...
, Professor's Cube
Professor's Cube
The Professor's Cube is a mechanical puzzle, a 5×5×5 version of the Rubik's Cube. It has qualities in common with both the original 3×3×3 Rubik's Cube and the 4×4×4 Rubik's Revenge, and knowing the solution to either can help when working on the 5×5×5 cube....
, V-Cube 6
V-Cube 6
The V-Cube 6 is the 6×6×6 version of Rubik's Cube. Unlike the original puzzle , it has no fixed facets: the center facets are free to move to different positions...
, Pocket Cube
Pocket Cube
The Pocket Cube is the 2×2×2 equivalent of a Rubik's Cube. The cube consists of 8 pieces, all corners.-Permutations:...
, original Rubik's Cube, Rubik's Revenge
Rubik's Revenge
The Rubik's Revenge is the 4×4×4 version of Rubik's Cube. Invented by Péter Sebestény, the Rubik's Revenge was nearly called the Sebestény Cube until a somewhat last-minute decision changed the puzzle's name to attract fans of the original Rubik's Cube...
. Clicking on a cube in the picture will redirect to the respective cube's page.
default none

poly 964 370 1082 448 1065 545 970 622 865 545 875 445 Pocket Cube
Pocket Cube
The Pocket Cube is the 2×2×2 equivalent of a Rubik's Cube. The cube consists of 8 pieces, all corners.-Permutations:...
poly 620 370 844 363 862 536 850 680 628 682 Rubik's Cube
Rubik's Cube
Rubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...
poly 455 280 570 440 580 605 355 705 255 530 220 363 Rubik's Revenge
Rubik's Revenge
The Rubik's Revenge is the 4×4×4 version of Rubik's Cube. Invented by Péter Sebestény, the Rubik's Revenge was nearly called the Sebestény Cube until a somewhat last-minute decision changed the puzzle's name to attract fans of the original Rubik's Cube...
poly 540 75 780 90 780 225 760 360 620 365 605 420 560 420 505 340 500 235 Professor's Cube
Professor's Cube
The Professor's Cube is a mechanical puzzle, a 5×5×5 version of the Rubik's Cube. It has qualities in common with both the original 3×3×3 Rubik's Cube and the 4×4×4 Rubik's Revenge, and knowing the solution to either can help when working on the 5×5×5 cube....
poly 890 50 1125 90 1065 420 1040 420 965 365 930 390 850 380 845 365 830 360 840 205 V-Cube 6
V-Cube 6
The V-Cube 6 is the 6×6×6 version of Rubik's Cube. Unlike the original puzzle , it has no fixed facets: the center facets are free to move to different positions...
poly 255 50 320 90 405 225 420 290 210 360 230 460 210 465 150 410 90 320 60 240 45 155 120 100 190 70 V-Cube 7
V-Cube 7
The V-Cube 7 is the 7×7×7 version of Rubik's Cube. It was invented by Panagiotis Verdes and is produced by his company, Verdes Innovations SA. Like the 5×5×5, the V-Cube 7 has both fixed and movable center facets.- Mechanics :...
There are different variations of Rubik's Cubes with up to seven layers: the 2×2×2 (Pocket/Mini Cube
Pocket Cube
The Pocket Cube is the 2×2×2 equivalent of a Rubik's Cube. The cube consists of 8 pieces, all corners.-Permutations:...
), the standard 3×3×3 cube, the 4×4×4 (Rubik's Revenge/Master Cube
Rubik's Revenge
The Rubik's Revenge is the 4×4×4 version of Rubik's Cube. Invented by Péter Sebestény, the Rubik's Revenge was nearly called the Sebestény Cube until a somewhat last-minute decision changed the puzzle's name to attract fans of the original Rubik's Cube...
), and the 5×5×5 (Professor's Cube
Professor's Cube
The Professor's Cube is a mechanical puzzle, a 5×5×5 version of the Rubik's Cube. It has qualities in common with both the original 3×3×3 Rubik's Cube and the 4×4×4 Rubik's Revenge, and knowing the solution to either can help when working on the 5×5×5 cube....
), the 6×6×6 (V-Cube 6
V-Cube 6
The V-Cube 6 is the 6×6×6 version of Rubik's Cube. Unlike the original puzzle , it has no fixed facets: the center facets are free to move to different positions...
), and 7×7×7 (V-Cube 7
V-Cube 7
The V-Cube 7 is the 7×7×7 version of Rubik's Cube. It was invented by Panagiotis Verdes and is produced by his company, Verdes Innovations SA. Like the 5×5×5, the V-Cube 7 has both fixed and movable center facets.- Mechanics :...
).
CESailor Tech's E-cube is an electronic variant of the 3×3×3 cube, made with RGB LEDs and switches. There are two switches on each row and column. Pressing the switches indicates the direction of rotation, which causes the LED display to change colours, simulating real rotations. The product was demonstrated at the Taiwan government show of college designs on October 30, 2008.
Another electronic variation of the 3×3×3 Cube is the Rubik's TouchCube. Sliding a finger across its faces causes its patterns of coloured lights to rotate the same way they would on a mechanical cube. The TouchCube was introduced at the American International Toy Fair
American International Toy Fair
The American International Toy Fair is one of a few major toy industry trade shows held around the world. It is held annually in mid February in New York City's Toy Center, located at 23rd Street at the crossover of Fifth Avenue and Broadway and at the Jacob K. Javits Convention Center, and is...
in New York on February 15, 2009.
The Cube has inspired an entire category of similar puzzles, commonly referred to as twisty puzzles
Combination puzzles
A combination puzzle, also known as a sequential move puzzle, is a puzzle which consists of a set of pieces which can be manipulated into different combinations by a group of operations. The puzzle is solved by achieving a particular combination starting from a random combination...
, which includes the cubes of different sizes mentioned above as well as various other geometric shapes. Some such shapes include the tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
(Pyraminx
Pyraminx
The Pyraminx is a tetrahedral puzzle similar to the Rubik's Cube. It was invented and patented by Uwe Meffert, and introduced by Tomy Toys of Japan in 1981. Meffert continues to sell it in his toy shop, ....
), the octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
(Skewb Diamond
Skewb Diamond
The Skewb Diamond is an octahedron-shaped puzzle similar to the Rubik's Cube. It has 14 movable pieces which can be rearranged in a total of 138,240 possible combinations. This puzzle is the dual polyhedron of the Skewb.- Description :...
), the dodecahedron (Megaminx
Megaminx
The Megaminx is a dodecahedron-shaped puzzle similar to the Rubik's Cube. It has a total of 50 movable pieces to rearrange, compared to the 20 movable pieces of the Rubik's cube.- History :...
), the icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
(Dogic
Dogic
The Dogic is an icosahedron-shaped puzzle like the Rubik's cube. The 5 triangles meeting at its tips may be rotated, or 5 entire faces around the tip may be rotated. It has a total of 80 movable pieces to rearrange, compared to the 20 pieces in the Rubik's cube.- History :The Dogic was patented by...
). There are also puzzles that change shape such as Rubik's Snake
Rubik's Snake
A Rubik's Snake is a toy with twenty-four wedges identically shaped liked prisms, specifically right isosceles triangular prisms. The wedges are connected, by spring bolts, such that they can be twisted, but not separated...
and the Square One
Square one (puzzle)
The Square One, also known as Back to Square One and Cube 21, is a puzzle similar to the Rubik's Cube. Its distinguishing feature among the numerous Rubik's Cube variants is that it can change shape as it is twisted, due to the way it is cut, thus adding an extra level of challenge and difficulty...
.
Custom-built puzzles
In the past, puzzles have been built resembling the Rubik's Cube or based on its inner workings. For example, a cuboid is a puzzle based on the Rubik's Cube, but with different functional dimensions, such as, 2×2×4, 2×3×4, 3×3×5. Many cuboids are based on 4×4×4 or 5×5×5 mechanisms, via building plastic extensions or by directly modifying the mechanism itself.Some custom puzzles are not derived from any existing mechanism, such as the Gigaminx v1.5-v2, Bevel Cube, SuperX, Toru, Rua, and 1×2×3. These puzzles usually have a set of masters 3D printed, which then are copied using molding and casting techniques to create the final puzzle.
Other Rubik's Cube modifications include cubes that have been extended or truncated to form a new shape. An example of this is the Trabjer's Octahedron, which can be built by truncating and extending portions of a regular 3×3. Most shape mods can be adapted to higher-order cubes. In the case of Tony Fisher's Rhombic Dodecahedron, there are 3×3, 4×4, 5×5, and 6×6 versions of the puzzle.
Rubik's Cube software


Popular culture
Many movies and TV shows have featured characters that solve Rubik's Cubes quickly to establish their high intelligence. Rubik's Cubes also regularly feature as motifs in works of art.See also
- Cubage (video game)Cubage (video game)Cubage is a video game developed by the FV Productions, and released in November, 2008 for Xbox360.-Overview:Cubage is a digital version of the wildly popular Rubik's Cube.-Gameplay:...
- n-dimensional sequential move puzzle
- OctacubeOctacubeOctacube is a type of mind-teaser puzzle made up of eight cubes with colors on the faces. The object of the puzzle is to arrange the eight cubes into a 2×2×2 cube such that all faces show the same color on the inside and all external colors which magneticly touch are the same color...
- Rubik, the Amazing CubeRubik, the Amazing CubeRubik, the Amazing Cube was a Saturday morning cartoon that aired from 10 September 1983–1 September 1984 in the United States, produced by Ruby-Spears Productions. The program, broadcast as part of The Pac-Man/Rubik, the Amazing Cube Hour block on ABC, featured a magic Rubik’s Cube named Rubik...
- Rubik's DominoRubik's DominoRubik's Domino is a hand-held game similar to a Rubik's Cube. However, it is missing a layer, making it a 2×3×3 cuboid. The 3x3 faces can be turned 90-degrees as normal, but the 2x3 faces can only be turned 180 degrees. Other cuboids of 2x2xn will solve like multiple Dominoes at once. The original...

