Rowbottom cardinal
Encyclopedia
In set theory
, a Rowbottom cardinal, introduced by , is a certain kind of large cardinal number.
An uncountable
cardinal number
κ is said to be Rowbottom if for every function f: [κ]<ω → λ (where λ < κ) there is a set H of order type κ that is quasi-homogeneous for f, i.e., for every n, the f-image of the set of n-element subsets of H has countably many elements.
Every Ramsey cardinal
is Rowbottom, and every Rowbottom cardinal is Jónsson
. By a theorem of Kleinberg, the theories ZFC + “there is a Rowbottom cardinal” and ZFC + “there is a Jónsson cardinal” are equiconsistent.
In general, Rowbottom cardinals need not be large cardinals in the usual sense: Rowbottom cardinals could be singular. It is an open question whether ZFC + “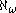
is Rowbottom” is consistent. If it is, it has much higher consistency strength than the existence of a Rowbottom cardinal. The axiom of determinacy
does imply that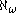
is Rowbottom (but contradicts the axiom of choice).
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a Rowbottom cardinal, introduced by , is a certain kind of large cardinal number.
An uncountable
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
κ is said to be Rowbottom if for every function f: [κ]<ω → λ (where λ < κ) there is a set H of order type κ that is quasi-homogeneous for f, i.e., for every n, the f-image of the set of n-element subsets of H has countably many elements.
Every Ramsey cardinal
Ramsey cardinal
In mathematics, a Ramsey cardinal is a certain kind of large cardinal number introduced by and named after Frank P. Ramsey.With [κ]<ω denoting the set of all finite subsets of κ, a cardinal number κ such that for every function...
is Rowbottom, and every Rowbottom cardinal is Jónsson
Jónsson cardinal
In set theory, a Jónsson cardinal is a certain kind of large cardinal number.An uncountable cardinal number κ is said to be Jónsson if for every function f: [κ]...
. By a theorem of Kleinberg, the theories ZFC + “there is a Rowbottom cardinal” and ZFC + “there is a Jónsson cardinal” are equiconsistent.
In general, Rowbottom cardinals need not be large cardinals in the usual sense: Rowbottom cardinals could be singular. It is an open question whether ZFC + “
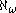is Rowbottom” is consistent. If it is, it has much higher consistency strength than the existence of a Rowbottom cardinal. The axiom of determinacyAxiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
does imply that
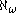is Rowbottom (but contradicts the axiom of choice).