Robert M. Solovay
Encyclopedia
Robert Martin Solovay is an American
mathematician
specializing in set theory
.
Solovay earned his Ph.D.
from the University of Chicago
in 1964 under the direction of Saunders Mac Lane
, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem
. Solovay has spent his career at the University of California
at Berkeley, where his notable Ph.D. students include W. Hugh Woodin
and Matthew Foreman
.
Solovay's noted accomplishments include:
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
specializing in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
.
Solovay earned his Ph.D.
Ph.D.
A Ph.D. is a Doctor of Philosophy, an academic degree.Ph.D. may also refer to:* Ph.D. , a 1980s British group*Piled Higher and Deeper, a web comic strip*PhD: Phantasy Degree, a Korean comic series* PhD Docbook renderer, an XML renderer...
from the University of Chicago
University of Chicago
The University of Chicago is a private research university in Chicago, Illinois, USA. It was founded by the American Baptist Education Society with a donation from oil magnate and philanthropist John D. Rockefeller and incorporated in 1890...
in 1964 under the direction of Saunders Mac Lane
Saunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem
Riemann–Roch theorem
The Riemann–Roch theorem is an important tool in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles...
. Solovay has spent his career at the University of California
University of California
The University of California is a public university system in the U.S. state of California. Under the California Master Plan for Higher Education, the University of California is a part of the state's three-tier public higher education system, which also includes the California State University...
at Berkeley, where his notable Ph.D. students include W. Hugh Woodin
W. Hugh Woodin
William Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...
and Matthew Foreman
Matthew Foreman
Matthew Dean Foreman is a set theorist at University of California, Irvine. He has made contributions in widely varying areas of set theory, including descriptive set theory, forcing, and infinitary combinatorics....
.
Solovay's noted accomplishments include:
- Solovay's theorem showing that, if one assumes the existence of an inaccessible cardinalInaccessible cardinalIn set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
, that the statement "every set of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is Lebesgue measurable" is consistent with ZF without the axiom of choice; - Isolating the notion of 0#Zero sharpIn the mathematical discipline of set theory, 0# is the set of true formulas about indiscernibles in the Gödel constructible universe. It is often encoded as a subset of the integers , or as a subset of the hereditarily finite sets, or as a real number...
; - Proving that the existence of a real valued measurable cardinal is equiconsistentEquiconsistencyIn mathematical logic, two theories are equiconsistent if, roughly speaking, they are "as consistent as each other".It is not in general possible to prove the absolute consistency of a theory T...
with the existence of a measurable cardinal; - Proving that if
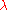is a strong limit singular cardinal, greater than a strongly compact cardinalStrongly compact cardinalIn mathematical set theory, a strongly compact cardinal is a certain kind of large cardinal number; their existence can neither be proven nor disproven from the standard axioms of set theory....
then
holds; - Proving that if
is an uncountable regular cardinal, and 
is a stationary setStationary setIn mathematics, particularly in set theory and model theory, there are at least three notions of stationary set:-Classical notion:If \kappa \, is a cardinal of uncountable cofinality, S \subseteq \kappa \,, and S \, intersects every club set in \kappa \,, then S \, is called a stationary set....
, then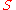
can be decomposed into the union of 
disjoint stationary sets; - Outside of set theory, developing (with Volker StrassenVolker StrassenVolker Strassen is a German mathematician, a professor emeritus in the department of mathematics and statistics at the University of Konstanz.-Biography:Strassen was born on April 29, 1936, in Düsseldorf-Gerresheim....
) the Solovay-Strassen primality testSolovay-Strassen primality testThe Solovay–Strassen primality test, developed by Robert M. Solovay and Volker Strassen, is a probabilistic test to determine if a number is composite or probably prime...
, used to identify large natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s that are primePrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
with high probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
. This method has had important ramifications for cryptographyCryptographyCryptography is the practice and study of techniques for secure communication in the presence of third parties...
.