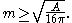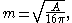Riemannian Penrose inequality
Encyclopedia
In mathematical general relativity
, the Penrose inequality, first conjectured by Sir Roger Penrose
, estimates the mass of a spacetime
in terms of the total area of its black holes and is a generalization of the positive mass theorem. The Riemannian Penrose inequality is the most important special case. Specifically, if (M, g) is an asymptotically flat Riemannian 3-manifold
with nonnegative scalar curvature
and ADM mass m, and A is the area of the outermost minimal surface
(possibly with multiple connected components), then the Riemannian Penrose inequality asserts
This is purely a geometrical fact, and it corresponds to the case of a complete three-dimensional, space-like, totally geodesic submanifold
of a (3 + 1)-dimensional spacetime. Such a submanifold is often called a time-symmetric initial data set for a spacetime. The condition of (M, g) having nonnegative scalar curvature is equivalent to the spacetime obeying the dominant energy condition.
This inequality was first proved by Gerhard Huisken and Tom Ilmanen in 1997 in the case where A is the area of the largest component of the outermost minimal surface. Their proof relied on the machinery of weakly defined inverse mean curvature flow
, which they developed. In 1999, Hubert Bray gave the first complete proof of the above inequality using a conformal flow
of metrics. Both of the papers were published in 2001.
.
then the manifold in question is isometric to a slice of the Schwarzschild spacetime outside of the outermost minimal surface.
condition, and nonnegative scalar curvature
is replaced with the dominant energy condition. Proving such an inequality remains an open problem in general relativity, called the Penrose Conjecture.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the Penrose inequality, first conjectured by Sir Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
, estimates the mass of a spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
in terms of the total area of its black holes and is a generalization of the positive mass theorem. The Riemannian Penrose inequality is the most important special case. Specifically, if (M, g) is an asymptotically flat Riemannian 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
with nonnegative scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
and ADM mass m, and A is the area of the outermost minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
(possibly with multiple connected components), then the Riemannian Penrose inequality asserts
This is purely a geometrical fact, and it corresponds to the case of a complete three-dimensional, space-like, totally geodesic submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of a (3 + 1)-dimensional spacetime. Such a submanifold is often called a time-symmetric initial data set for a spacetime. The condition of (M, g) having nonnegative scalar curvature is equivalent to the spacetime obeying the dominant energy condition.
This inequality was first proved by Gerhard Huisken and Tom Ilmanen in 1997 in the case where A is the area of the largest component of the outermost minimal surface. Their proof relied on the machinery of weakly defined inverse mean curvature flow
Inverse mean curvature flow
In the field of differential geometry in mathematics, inverse mean curvature flow is an example of a geometric flow of hypersurfaces a Riemannian manifold...
, which they developed. In 1999, Hubert Bray gave the first complete proof of the above inequality using a conformal flow
Geometric flow
In mathematics, specifically differential geometry, a geometric flow is the gradient flow associated to a functional on a manifold which has a geometric interpretation, usually associated with some extrinsic or intrinsic curvature...
of metrics. Both of the papers were published in 2001.
Physical Motivation
The original physical argument that led Penrose to conjecture such an inequality invoked the Hawking area theorem and the Cosmic censorship hypothesisCosmic censorship hypothesis
The weak and the strong cosmic censorship hypotheses are two mathematical conjectures about the structure of singularities arising in general relativity....
.
Case of Equality
Both the Bray and Huisken-Ilmanen proofs of the Riemannian Penrose inequality state that under the hypotheses, ifthen the manifold in question is isometric to a slice of the Schwarzschild spacetime outside of the outermost minimal surface.
Penrose Conjecture
More generally, Penrose conjectured that an inequality as above should hold for spacelike submanifolds of spacetimes that are not necessarily time-symmetric. In this case, the minimal surface condition is replaced with an apparent horizonApparent horizon
In general relativity, an apparent horizon is a surface that is the boundary between light rays that are directed outwards and moving outwards, and those directed outwards but moving inwards.Apparent horizons are not invariant properties of a spacetime...
condition, and nonnegative scalar curvature
is replaced with the dominant energy condition. Proving such an inequality remains an open problem in general relativity, called the Penrose Conjecture.