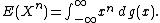Riemann-Stieltjes integral
Encyclopedia
In mathematics
, the Riemann–Stieltjes integral is a generalization of the Riemann integral
, named after Bernhard Riemann
and Thomas Joannes Stieltjes
.
of a real
-valued function ƒ of a real variable with respect to a real function g is denoted by
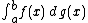
and defined to be the limit, as the mesh
of the partition
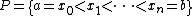
of the interval [a, b] approaches zero, of the approximating sum
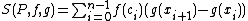
where ci is in the i-th subinterval [xi, xi+1]. The two functions ƒ and g are respectively called the integrand and the integrator.
The "limit" is here understood to be a number A (the value of the Riemann–Stieltjes integral) such that for every ε > 0, there exists δ > 0 such that for every partition P with mesh(P) < δ, and for every choice of points ci in [xi, xi+1],
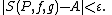
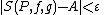
for every choice of points ci in [xi, xi+1].
This generalization exhibits the Riemann–Stieltjes integral as the Moore–Smith limit on the directed set
of partitions of [a, b] . calls it the Pollard–Moore–Stieltjes integral.
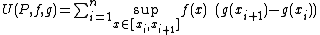
and the lower sum by
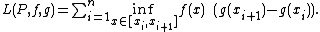
If g is a nondecreasing function on [a, b], then the generalized Riemann–Stieltjes of ƒ with respect to g exists if and only if, for every ε > 0, there exists a partition P such that
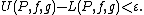
Furthermore, ƒ is Riemann–Stieltjes integrable with respect to g (in the classical sense) if
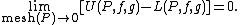
See .
of
given by
for example, if the derivative is unbounded. But if the derivative is continuous, they will be the same. This condition is also satisfied if g is the (Lebesgue) integral of its derivative; in this case g is said to be absolutely continuous.
However, g may have jump discontinuities, or may have derivative zero almost everywhere while still being continuous and increasing (for example, g could be the Cantor function
), in either of which cases the Riemann–Stieltjes integral is not captured by any expression involving derivatives of g.
The Riemann–Stieltjes integral admits integration by parts
in the form
and the existence of either integral implies the existence of the other .
on [a, b], then the integral exists. A function g is of bounded variation if and only if it is the difference between two monotone functions. If g is not of bounded variation, then there will be continuous functions which cannot be integrated with respect to g. In general, the integral is not well-defined if f and g share any points of discontinuity, but this sufficient condition is not necessary.
On the other hand, a classical result of states that the integral is well-defined if f is α-Hölder continuous and g is β-Hölder continuous with α + β > 1.
of a random variable
X that has a probability density function
with respect to Lebesgue measure
, and f is any function for which the expected value
E(|f(X)|) is finite, then the probability density function of X is the derivative of g and we have
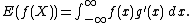
But this formula does not work if X does not have a probability density function with respect to Lebesgue measure. In particular, it does not work if the distribution of X is discrete (i.e., all of the probability is accounted for by point-masses), and even if the cumulative distribution function g is
continuous, it does not work if g fails to be absolutely continuous
(again, the Cantor function
may serve as an example of this failure). But the identity
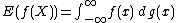
holds if g is any cumulative probability distribution function on the real line, no matter how ill-behaved. In particular, no matter how ill-behaved the cumulative distribution function g of a random variable X, if the moment
E(Xn) exists, then it is equal to
of the Banach space
C[a,b] of continuous functions in an interval [a,b] as Riemann–Stieltjes integrals against functions of bounded variation
. Later, that theorem was reformulated in terms of measures.
The Riemann–Stieltjes integral also appears in the formulation of the spectral theorem
for (non-compact) self-adjoint (or more generally, normal) operators in a Hilbert space. In this theorem, the integral is considered with respect to a spectral family of projections. See for details.
Riemann–Stieltjes integrals are allowed, the Lebesgue integral is not strictly more general than the Riemann–Stieltjes integral.
The Riemann–Stieltjes integral also generalizes to the case when either the integrand ƒ or the integrator g take values in a Banach space
. If takes values in the Banach space X, then it is natural to assume that it is of strongly bounded variation, meaning that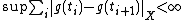
the supremum being taken over all finite partitions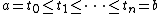
of the interval [a,b]. This generalization plays a role in the study of semigroups
, via the Laplace–Stieltjes transform.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Riemann–Stieltjes integral is a generalization of the Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
, named after Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
and Thomas Joannes Stieltjes
Thomas Joannes Stieltjes
Thomas Joannes Stieltjes was a Dutch mathematician. He was born in Zwolle and died in Toulouse, France. He was a pioneer in the field of moment problems and contributed to the study of continued fractions....
.
Definition
The Riemann–Stieltjes integralIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued function ƒ of a real variable with respect to a real function g is denoted by
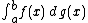
and defined to be the limit, as the mesh
Partition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
of the partition
Partition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
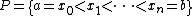
of the interval [a, b] approaches zero, of the approximating sum
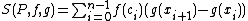
where ci is in the i-th subinterval [xi, xi+1]. The two functions ƒ and g are respectively called the integrand and the integrator.
The "limit" is here understood to be a number A (the value of the Riemann–Stieltjes integral) such that for every ε > 0, there exists δ > 0 such that for every partition P with mesh(P) < δ, and for every choice of points ci in [xi, xi+1],
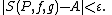
Generalized Riemann–Stieltjes integral
A slight generalization, introduced by and now standard in analysis, is to consider in the above definition partitions P that refine another partition Pε, meaning that P arises from Pε by the addition of points, rather than from partitions with a finer mesh. Specifically, the generalized Riemann–Stieltjes integral of ƒ with respect to g is a number A such that for every ε > 0 there exists a partition Pε such that for every partition P that refines Pε,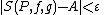for every choice of points ci in [xi, xi+1].
This generalization exhibits the Riemann–Stieltjes integral as the Moore–Smith limit on the directed set
Directed set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
of partitions of [a, b] . calls it the Pollard–Moore–Stieltjes integral.
Darboux sums
The Riemann–Stieltjes integral can be efficiently handled using an appropriate generalization of Darboux sums. For a partition P define the upper Darboux sum of ƒ with respect to g by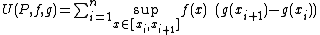and the lower sum by
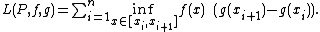
If g is a nondecreasing function on [a, b], then the generalized Riemann–Stieltjes of ƒ with respect to g exists if and only if, for every ε > 0, there exists a partition P such that
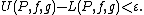
Furthermore, ƒ is Riemann–Stieltjes integrable with respect to g (in the classical sense) if
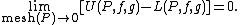
See .
Properties and relation to the Riemann integral
If g should happen to be everywhere differentiable, then the Riemann–Stieltjes integral may still be different from the Riemann integralRiemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
of
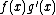given byfor example, if the derivative is unbounded. But if the derivative is continuous, they will be the same. This condition is also satisfied if g is the (Lebesgue) integral of its derivative; in this case g is said to be absolutely continuous.
However, g may have jump discontinuities, or may have derivative zero almost everywhere while still being continuous and increasing (for example, g could be the Cantor function
Cantor function
In mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
), in either of which cases the Riemann–Stieltjes integral is not captured by any expression involving derivatives of g.
The Riemann–Stieltjes integral admits integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
in the form
and the existence of either integral implies the existence of the other .
Existence of the integral
The best simple existence theorem states that if f is continuous and g is of bounded variationBounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
on [a, b], then the integral exists. A function g is of bounded variation if and only if it is the difference between two monotone functions. If g is not of bounded variation, then there will be continuous functions which cannot be integrated with respect to g. In general, the integral is not well-defined if f and g share any points of discontinuity, but this sufficient condition is not necessary.
On the other hand, a classical result of states that the integral is well-defined if f is α-Hölder continuous and g is β-Hölder continuous with α + β > 1.
Application to probability theory
If g is the cumulative probability distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X that has a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
with respect to Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, and f is any function for which the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
E(|f(X)|) is finite, then the probability density function of X is the derivative of g and we have
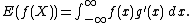
But this formula does not work if X does not have a probability density function with respect to Lebesgue measure. In particular, it does not work if the distribution of X is discrete (i.e., all of the probability is accounted for by point-masses), and even if the cumulative distribution function g is
continuous, it does not work if g fails to be absolutely continuous
Absolute continuity
In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
(again, the Cantor function
Cantor function
In mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
may serve as an example of this failure). But the identity
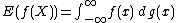
holds if g is any cumulative probability distribution function on the real line, no matter how ill-behaved. In particular, no matter how ill-behaved the cumulative distribution function g of a random variable X, if the moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
E(Xn) exists, then it is equal to
Application to functional analysis
The Riemann–Stieltjes integral appears in the original formulation of F. Riesz's theorem which represents the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
C[a,b] of continuous functions in an interval [a,b] as Riemann–Stieltjes integrals against functions of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
. Later, that theorem was reformulated in terms of measures.
The Riemann–Stieltjes integral also appears in the formulation of the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
for (non-compact) self-adjoint (or more generally, normal) operators in a Hilbert space. In this theorem, the integral is considered with respect to a spectral family of projections. See for details.
Generalization
An important generalization is the Lebesgue–Stieltjes integral which generalizes the Riemann–Stieltjes integral in a way analogous to how the Lebesgue integral generalizes the Riemann integral. If improperImproper integral
In calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....
Riemann–Stieltjes integrals are allowed, the Lebesgue integral is not strictly more general than the Riemann–Stieltjes integral.
The Riemann–Stieltjes integral also generalizes to the case when either the integrand ƒ or the integrator g take values in a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. If takes values in the Banach space X, then it is natural to assume that it is of strongly bounded variation, meaning that
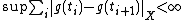
the supremum being taken over all finite partitions
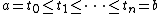
of the interval [a,b]. This generalization plays a role in the study of semigroups
C0-semigroup
In mathematics, a C0-semigroup, also known as a strongly continuous one-parameter semigroup, is a generalization of the exponential function...
, via the Laplace–Stieltjes transform.