
Resolution (algebra)
Encyclopedia
In mathematics
, particularly in abstract algebra
and homological algebra
, a resolution (or left resolution; dually a coresolution or right resolution) is a sequence of objects which is used to describe the structure of a module
, or, more generally, the structure of an object in an abelian category
.
Generally, if the objects involved in the sequence have a property P, then one speaks of a P resolution: for example, a flat resolution, a free resolution, an injective resolution, a projective resolution. However, a finite resolution is one where only finitely many of the objects in the sequence are non-zero.
(possibly infinite) of R-modules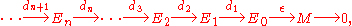
with all the Ei modules over R. The map ε is called an augmentation map. For succinctness, the resolution above can be written as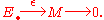
The dual notion
is that of a right resolution (or coresolution, or simply resolution). Specifically, given a module M over a ring R, a right resolution is a possibly infinite exact sequence of R-modules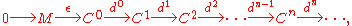
where each Ci is an R-module (it is common to use superscripts on the objects in the resolution and the maps between them to indicate the dual nature of such a resolution). For succinctness, the resolution above can be written as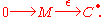
A (co)resolution is said to be finite if only finitely many of the modules involved are non-zero.
The definition of resolutions of an object M in abelian category A is the same as above, but the Ei and Ci are objects in A, and all maps involved are morphism
s in A.
s. A fortiori, every module admits a projective resolution. The minimal length of a finite projective resolution of a module M is called its projective dimension and denoted pd(M). If M does not admit a finite projective resolution then the projective dimension is infinite. Dually, every R-module possesses an injective resolution, i.e. a right resolution by injective module
s.
These results may not hold in a general abelian category A. If every object of A has a projective (resp. injective) resolution, then A is said to have enough projectives (resp. enough injectives).
K•(x).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, a resolution (or left resolution; dually a coresolution or right resolution) is a sequence of objects which is used to describe the structure of a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, or, more generally, the structure of an object in an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
.
Generally, if the objects involved in the sequence have a property P, then one speaks of a P resolution: for example, a flat resolution, a free resolution, an injective resolution, a projective resolution. However, a finite resolution is one where only finitely many of the objects in the sequence are non-zero.
Definition
Given a module M over a ring R, a left resolution (or simply resolution) of M is an exact sequenceExact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
(possibly infinite) of R-modules
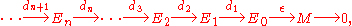
with all the Ei modules over R. The map ε is called an augmentation map. For succinctness, the resolution above can be written as
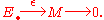
The dual notion
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
is that of a right resolution (or coresolution, or simply resolution). Specifically, given a module M over a ring R, a right resolution is a possibly infinite exact sequence of R-modules
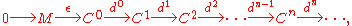
where each Ci is an R-module (it is common to use superscripts on the objects in the resolution and the maps between them to indicate the dual nature of such a resolution). For succinctness, the resolution above can be written as
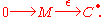
A (co)resolution is said to be finite if only finitely many of the modules involved are non-zero.
The definition of resolutions of an object M in abelian category A is the same as above, but the Ei and Ci are objects in A, and all maps involved are morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s in A.
Properties
Every R-module possesses a free left resolution: that is, a left resolution by free moduleFree module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
s. A fortiori, every module admits a projective resolution. The minimal length of a finite projective resolution of a module M is called its projective dimension and denoted pd(M). If M does not admit a finite projective resolution then the projective dimension is infinite. Dually, every R-module possesses an injective resolution, i.e. a right resolution by injective module
Injective module
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
s.
These results may not hold in a general abelian category A. If every object of A has a projective (resp. injective) resolution, then A is said to have enough projectives (resp. enough injectives).
Examples
A classic example of a projective resolution is given by the Koszul complexKoszul complex
In mathematics, the Koszul complex was first introduced to define a cohomology theory for Lie algebras, by Jean-Louis Koszul...
K•(x).

